Let us make an in-depth study of Elasticity of Demand. After reading this article you will learn about: 1. Concept of Elasticity of Demand 2. Types of Elasticity of Demand 3. Measurement 4. Factors Determining 5. Importance.
Concept of Elasticity of Demand:
The law of demand indicates the direction of change in quantity demanded to a change in price.
It states that when price falls, demand rises. But how much the quantity demanded rises (or falls) following a certain fall (or rise) in prices cannot be known from the law of demand. That is to say, how much quantity demanded changes following a change in the price of a commodity can be known from the concept of elasticity of demand?
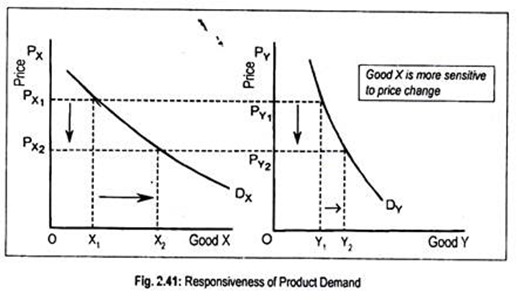
In Fig. 2.41, we have drawn two demand curves for good X and good Y. Both these curves are negative sloping. Let us assume that prices of both goods X and Y are PX1 and PY1 (note that PX1 = PY1). At price OPX1, a consumer demands OX1 and, at price OPY1, OY1 is demanded.
Now if prices of both X and Y decline by an identical amount to OPX2 and OPY2, quantity demanded for X and Y rises from OX1 to OX2 and from OY1 to OY2, respectively. But the change in quantity demanded for good X is greater than the change in quantity demanded for good Y. This means that good X is more sensitive or responsive to a change in its price than good Y. This is called elasticity of demand.
By elasticity of demand, we normally mean price elasticity of demand. (Price) elasticity of demand measures the degree of responsiveness of quantity demanded following a change in own price of the commodity, holding money income and prices of related goods constant.
(Price) elasticity of demand is the relative difference in the dependent variable (here, quantity) divided by the relative difference in independent variable (here, price). Alternatively, it is defined as the absolute value of the ratio of percentage change in price. Thus, the elasticity of demand is a relative concept.
The formula for calculating elasticity of demand is:
ADVERTISEMENTS:
EP = proportional changes in quantity demanded/proportional changes in price
= % changes in quantity demanded/changes in price
EP = |∆Q/Q/∆P/P|= |∆Q/∆P.P/Q|
The vertical lines in the formula denote that we take the absolute value of the ratio and ∆P and ∆Q denote the changes in price and quantity. Since both price and quantity move in opposite direction, EP must always be a negative number. Normally, we drop the negative sign and take the absolute value of EP by taking ‘mod’ (or use negative sign by dropping vertical lines).
ADVERTISEMENTS:
Or absolute value, denoted by ||, turns the negative number into a positive one. Thus, EP = |- 5%/2%| = 2.51 = 2.5. Price elasticity is a pure number, independent of units of measure. The percentage will be the same whether we measure quantity demanded in numbers or kilograms or liters.
Types of Own (Price) Elasticity of Demand:
For all types of commodities, the rate of change of quantity demanded to a change in own price is not uniform. For some commodities, demand is said to be more responsive to price changes compared to other commodities. That is why there are various types of elasticities of demand.
They are of the following five types:
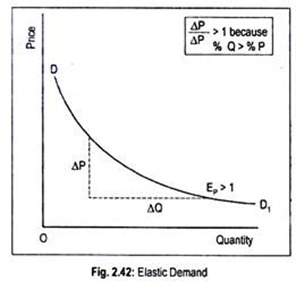
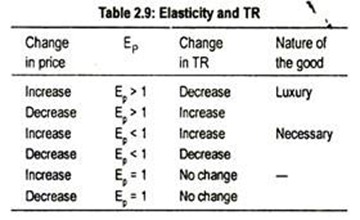
(1) Elastic Demand (EP > 1):
Demand is said to be elastic if the change in price causes a more than proportionate change in quantity demanded. A 10 p.c. change in price causes quantity demanded to change by more than 10 p.c. In other words, if E is greater than one, demand is said to be elastic (Fig. 2.42).
Normally, demand is elastic for luxury goods. Let the price of gold per gm decline from Rs. 160 to Rs. 140. As a result, demand for gold rises from 1,000 kilograms to 2,000 kilograms. Thus,
EP = 1,000/1,000 ÷ 20/160 = 1,000/20 .160/1,000 = 8
Since elasticity of demand for gold is greater than one, gold is a luxury item.
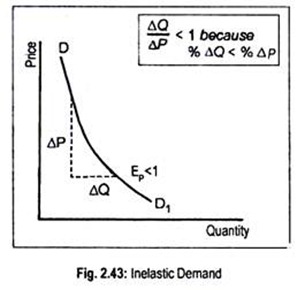
(2) Inelastic Demand (EP < 1):
When the change in price causes a less than proportionate change in quantity demanded, demand is inelastic. A 10 p.c. cut in price may cause quantity demanded to fall by, say, 1 p.c. Thus, demand is said to be inelastic (Ep< 1), shown in Fig. 2.43. Usually, demand is inelastic for necessary goods.
Suppose that following a drop in the price of wheat from paisa 40 per kilogram to paisa 20 per kilogram, demand for wheat rises from 1,600 kilograms to 2,000 kilograms. This means
EP = 400/160 ÷ 20/40 = 400/20. 40/1,600 = 0.5
Thus, wheat has an inelastic demand since EP < 1 and wheat is a necessary article.
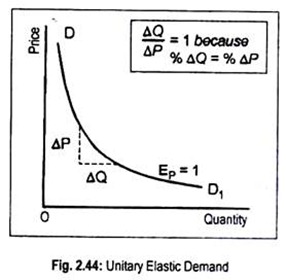
(3) Unit elasticity of Demand (EP = 1):
When the change in price causes the same proportionate change in quantity demanded, demand has unit elasticity. A 10 p.c. decline in price will lead to an exactly 10 p.c. increase in quantity demanded. Then EP = 1 (Fig. 2.44).
ADVERTISEMENTS:
Suppose that the price of a commodity declines from Rs. 200 to Rs. 100 per kilogram. As a result, demand for that commodity rises from 400 kilograms to 800 kilograms. Thus,
EP = 400/400 ÷ 100/100 = 400/100. 100/400 = 1
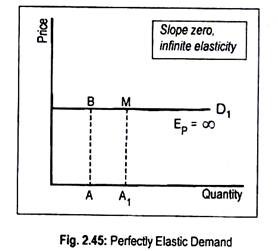
(4) Perfectly Elastic Demand (EP = ∞)
When a slight change in price causes a great change in quantity demanded, the value of elasticity of demand tends to be infinity and demand is said to be infinite or perfectly elastic. In this case, the demand curve (DD,) becomes parallel to the horizontal axis (Fig. 2.45). Under perfectly competitive market, the demand curve for a product of an individual firm becomes perfectly elastic.
ADVERTISEMENTS:
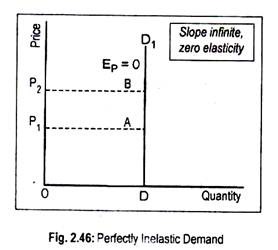
(5) Perfectly Inelastic Demand (EP = 0):
If quantity demanded becomes completely unresponsive to price changes, the coefficient tends to be zero. In this case, whatever the price, even if it is zero, quantity demanded will remain fixed at a particular level. The demand curve, thus, becomes parallel to the vertical axis (Fig. 2.46) and demand is said to be completely (perfectly) inelastic.
Thus, elasticity of demand varies from zero to infinity.
Measurement of Elasticity of Demand:
There are three methods of measuring elasticity of demand. These are:
(a) Total outlay (revenue) method
(b) Point elasticity method
ADVERTISEMENTS:
(c) Arc elasticity method
All these methods are described below:
1. Elasticity and Total Revenue or Outlay Method:
Marshall offered the method of total revenue or total outlay for estimating elasticity of demand. What the sellers receive from the sale of commodities is called total expenditure or outlay of buyers. There is no difference between total revenue and total outlay since what is spent by the buyers is received as income by the sellers.
Thus, total outlay/revenue is the price multiplied by the quantity purchases, i.e., TR = P × Q. Here we want to measure how much total outlay changes following a change in price. It depends upon the elasticity of demand.
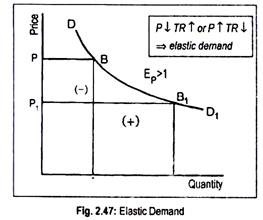
(a) Elastic Demand:
Suppose price declines (rises). As a result, total expenditure rises (falls). Under the circumstance, the value of elasticity of demand becomes greater than one. In Fig. 2.47, we have drawn a demand curve having a value of greater than one.
At a price OP, OA is demanded. Thus, the total expenditure equals OP × OA = rectangle OPBA. As price drops to OP1, the quantity demanded rises to OA1. Now, the total expenditure becomes OP1 × OA1 = rectangle OP1B1A1.
Since rectangle OP1B1A1 > rectangle OPBA, demand is said to be elastic. Remember: When price and total outlay move in opposite direction, demand for the product becomes elastic.
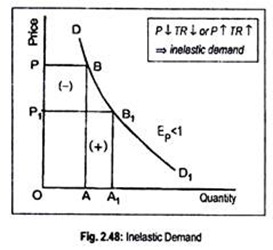
(b) Inelastic Demand:
If the total outlay falls when price falls, or if total outlay rises when price rises, then demand is said to be inelastic (i.e., Ep< 1). In Fig. 2.48, initial total outlay is OP1 × OA1 = rectangle OPBA. Now, if price falls, total outlay becomes OP1 × OA1 = rectangle OP1B1A1. Fig. 2.48 suggests that the rectangle OPBA is larger than the rectangle OP1B1A1. Hence, demand is inelastic.
(c) Unit Elasticity:
ADVERTISEMENTS:
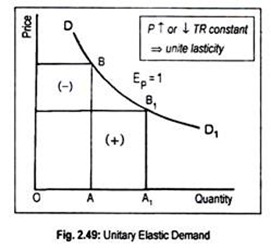
Irrespective of variations in demand and price, if the total outlay does not change, then demand is unit elastic (i.e., Ep = 1). In Fig. 2.49, we see that at price OP, total outlay is rectangle OPBA. When price declines to OP, total outlay becomes the area OP1B1A1.
Since rectangle OPBA = rectangle OP1B1A1, demand is said to have a unitary elasticity. The demand curve then looks like a rectangular hyperbola since the area of all the rectangles formed by the demand curve is always the same.
(d) Perfectly Elastic Demand:
In this case, at a particular price, any amount is demanded. Fig. 2.45 suggests that at a price OD, quantity demanded may be OA or OA1 or any amount. More revenue is earned at OA1 than at OA, although price is kept fixed.
(e) Perfectly Inelastic Demand:
ADVERTISEMENTS:
Fig. 2.46 tells us that as price rises, revenue rises. The vertical straight line demand curve says that, whatever the price, quantity demanded remains the same.
These relations between elasticity of demand and total outlay (P × Q = TR) may be presented here in a tabular form:
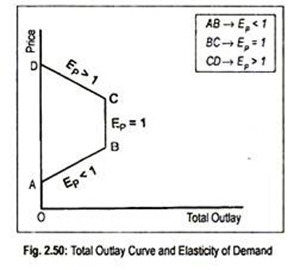
The relationship between elasticity and total outlay can also be explained in terms of Fig. 2.50 where we measure price of the commodity on the vertical axis and the total outlay on the horizontal axis. Here ABCD is the total outlay curve.
In the segment AB, demand is inelastic (Ep< 1), because price and total outlay move in the same direction. Demand is said to be elastic (Ep> 1) in the region CD since price and total outlay move in opposite direction. As total outlay remains invariant when price changes in the region BC, demand is unitary elastic.
2. Point Elasticity Method of Measurement:
When the change in price is infinitesimally small, Marshallian method may not provide accurate estimate of elasticity of demand. In that case, a geometrical method may be employed. This method aims at measuring elasticity of demand at a particular point on a demand curve.
So long, we tried to calculate the elasticity over certain area or segment of a demand curve and the terms elastic, inelastic and unit elastic had been applied to the whole demand curve. However, such is not true. It may happen that the demand for a product can be elastic in one price range and inelastic in another.
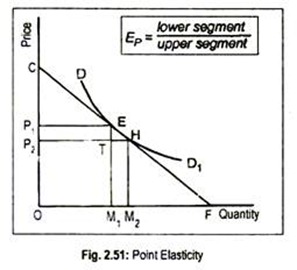
In fact, the degree of elasticity varies from one price range to another. So, it is better to calculate elasticity at a particular point on a demand curve to have an accurate estimate. This is explained in terms of Fig. 2.51.
Demand curve is DD1. To measure elasticity of demand at point E, we have drawn a straight line CF tangent to DD1 at point E. Points E and H are very close to each other. As price declines from OP1 to OP2, quantity demanded rises from OM1 to OM2.
The formula for elasticity of demand is:
EP = ∆Q/Q ÷ ∆P/P
The slope of the demand curve is:
∆P/∆Q = M1E /M1F
... ∆Q/∆P = M1F /M1E
The second component of the elasticity formula is:
P/Q = M1E /OM1
... EP = ∆Q/∆P. P/Q = M1F/M1E. M1E/OM1= M1F/OM1
Note that EM1F, CP1E and COF are similar triangles, the elasticity of demand curve DD1 at point E can be measured as:
... EP = M1F/OM1 = P1O/P1 = EF/EC
Thus, elasticity of demand at point E on a curvilinear demand curve DD1 is approximately equal to
EF/EC = lower segment of the demand curve/upper segment of the demand curve
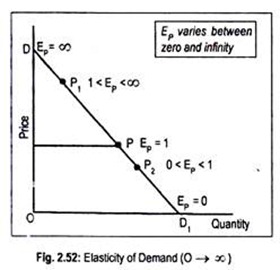
On the basis of this method of measurement, one can estimate elasticity of demand on a linear demand curve, shown in Fig. 2.52.
Here, DD1 is a linear demand curve. Elasticity of demand varies from point to point on a demand curve. At point P, elasticity of demand is PD1/PD. As the distance between PD1 and PD is the same, it is unit elastic (i.e., Ep = 1). As we move downwards along the curve DD1 from the mid-point, say point P2, elasticity declines. At P2 it is, inelastic (i.e., 0 < Ep< 1) since P2D1< P2D.
At point D1, elasticity is zero since 0/DD1is equal to zero. Further, as we move upwards from the mid-point, elasticity increases. At P1, it is elastic (i.e., 1 < Ep< ∞) since P1D1> P1D. On the other hand, at point D, it is infinite since DD1/0 is equal to infinity. Thus, at lower prices it is inelastic, and at higher prices it is elastic.
Thus, elasticity of demand on a straight line demand curve varies from zero to infinity (0 ≤ Ep ≤ ∞).
3. Arc Elasticity Method:
For very small movements in price and quantity, point elasticity method is an appropriate one. In other words, point elasticity method measures (price) elasticity of demand at a particular point on the demand curve. However, if price change is somewhat of a larger magnitude then geometrical method may give misleading estimate.
To avoid this problem, elasticity is measured over an arc of the demand curve. In other words, when we intend to estimate (price) elasticity of demand over some portion (i.e., the arc) of the demand curve, we then have arc elasticity method. Sometimes we know two prices and two quantities.
Under the circumstance, the point elasticity method may not provide good estimate. What is required in this case is the average elasticity of two prices and two quantities. This is called ‘arc’ elasticity, because it measures the average elasticity on an arc of a demand curve.
Suppose we have the following information about two prices and quantities:
Here changes in both price and quantity are much larger. Using old price (P1) and old quantity (Q1), one finds the value of elasticity of demand as:
EP = ∆Q /∆P. P1/Q1 = – 400/100. 60/400 = -6.0
When new price (P2) and new quantity (Q2) are taken into account, the coefficient becomes
EP = ∆Q /∆P. P2/Q2 = – 400/100. 50/800 = -2.5
Thus, estimation of elasticity in accordance with the formula for point elasticity method gives vastly different results. In other words, since elasticity of demand varies depending on the base, one should consider average price and average quantity demanded to calculate elasticity of demand.
That is to say, we want to measure average elasticity over an arc of the demand curve (i.e., mid-point or average, price and quantity):
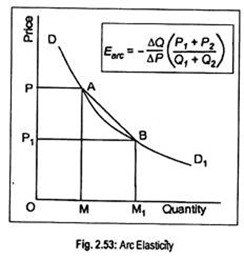
In terms of Fig. 2.53, we want to compute arc price elasticity of demand over the arc AB of the demand curve DD1. In other words, we want to measure elasticity between points A and B. The above formula measures arc elasticity over the straight line AB.
To do so, we have to take the average of prices (OP and OP1) and average of quantities (OM and OM1). Greater the convexity of the demand curve between A and B, one obtains almost perfect estimate of elasticity. Or greater the concavity of the demand curve between points A and B, the poorer the approximation of measurement of arc elasticity.
As we go on making the price change smaller and smaller, the arc of the demand curve may vanish or converge to a point. So, as a special case of arc elasticity, the concept of point elasticity becomes relevant.
Factors Determining Elasticity of Demand:
There are various factors on which elasticity of demand depends:
(a) Nature of the Commodity:
In the first place, it depends on the nature of the commodity. Commodities which are supposed to be essential or critical to our daily lives must have an inelastic demand, since price change of these items does not bring about a greater change in quantity demanded.
But, luxury goods have an elastic demand. Demand for these good can be quickly reduced when their prices rise. When their prices fall, consumers demand these goods in larger quantities. However, whether a particular commodity is a necessary or a luxury depends on income, tastes and preferences of the consumer.
A particular good may be necessary to someone having an inelastic demand. Same commodity may be elastic to another consumer. For instance, owning a TV may be a luxury item to a low income person. But the same may be bought as an essential item by a rich person.
(b) Availability of Substitutes:
Secondly, commodities having large number of substitutes must have an elastic demand. Some products, such as Horlicks, Complan, Viva, Maltova, Milo, etc., have quite a large number of close substitutes. A change in the price of, say, Horlicks—the prices of other substitutes remaining constant—will lead a consumer to substitute one beverage for another.
If the price of Horlicks goes down, buyers will demand more of it and less of its substitutes. Conversely, demand is fairly inelastic in the case of those commodities which do not have a large number of substitutes.
(c) Extent of Uses:
Thirdly, there are some commodities which can be used for a variety of purposes. For example, electricity. If price per unit of electricity consumed falls, people will reduce their consumption of its substitutes (e.g., coal, gas, etc.) and increase the consumption of electricity.
Coefficient of price elasticity of demand in this case must be greater than one. On the other hand, when a commodity is used only for one or two purposes, a price change will have less effect on its quantity demanded and, therefore, demand will be inelastic.
(d) Habit Good:
Fourthly, there are some commodities consumed out of habits and conventions— they have an elastic demand. Even in the face of rising prices of those commodities or falling income, people will consume those (such as, cigarette).
For this reason, price elasticity as well as income elasticity of demand for this type of commodity is inelastic. Further, gold ornaments are used in the marriage ceremony rather out of convention, though gold prices are rising. When gold is used in this way, its demand becomes inelastic.
(e) Time Dimension:
Fifthly, shorter the time, lower will be the elasticity of demand. This is because in the short run satisfactory substitutes of a product may not be available. Thus, demand for a product in the short run usually becomes inelastic. Such a commodity will be elastic in the long run when close substitutes may be produced.
Thus, the response of quantity demanded to a change in price will tend to be greater (smaller), the longer (shorter) the time-span considered. In the long run, there is enough time for adjustments to be made following a change in price.
(f) The Importance of being Unimportant:
Sixthly, people often pay little attention to the price of a product if it constitutes a relatively small part in their budget. For example, if the fire of railway ticket of a tourist who travels by rail once in a year is increased form Rs. 125 to Rs. 135, then he may not postpone his journey. This means he is unresponsive to such price hike and his demand is inelastic. This is called ‘the importance of being unimportant’.
(g) Durability:
Finally, durable commodities have an elastic demand. If the price of these goods rises, people will spend less on these goods. On the other hand, following a fall in the price of durable commodities (e.g., refrigerator), people demand more of them. In the case of non-durable commodities, demand is elastic.
Importance of the Concept of Elasticity of Demand:
The concept of elasticity of demand has both theoretical and practical value.
The concept may be used in understanding as well as tackling various economic problems:
(a) Price Determination:
Use of the concept of elasticity of demand is required in the price determination of a commodity under different market conditions. Under perfect competition, in the short run in which supply is absolutely inelastic price depends upon the elasticity of demand.
If demand suddenly falls—supply remaining fixed—prices will fall, and, if demand suddenly rises, prices will rise as output cannot be increased. Again, the stability of prices also depends on the elasticity of demand and elasticity of supply. If either the demand or the supply is elastic, fluctuations in prices will be within narrow limits.
Further, if the demand for an agricultural commodity is inelastic, increased production may spell disaster to the economic condition of farmers. So the government can adopt measures to save the plight of the farmers.
A monopoly seller must have a knowledge relating to the elasticity of demand for his product while determining the price of his commodity.
A monopolist will produce a commodity in the range of his demand curve where demand is said to be elastic. He will never produce in the range of the demand curve where demand is inelastic. Obviously, price determination of the monopoly product will be governed by the elasticity of demand.
(b) Wage Determination:
The concept of elasticity of demand is employed in wage determination. Wages, in modern days, are determined through the process of collective bargaining. Trade union will be successful in raising the wage rate provided labour demand is deemed to be inelastic. This is because of the fact that the degree of substitution between labour and other labour substituting inputs is less.
Trade union becomes cautious in demanding higher wage rates when the demand for labour is said to be elastic. Under the circumstance, the employer may be forced to employ more machines (assumed to be a cheaper input) than labour.
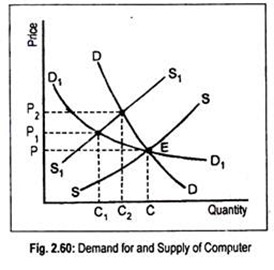
Anyway, this concept may be employed in analysing the problems connected with changes in the conditions of supply. Economists are interested in knowing the effect on employment in the software industry following a rise in the wages of workers engaged in this industry. We can answer this question in terms of Fig. 2.60.
Here DD is a rather inelastic demand curve whereas demand curve D1D1 is an elastic one. Both these demand curves intersect the supply curve, SS, at point E. Thus the equilibrium price is OP and equilibrium quantity demanded and supplied is OC.
Let there be an increase in the wages of workers in the computer industry. Consequently, the supply curve for computer will shift left to S1S1 and the price will rise to OP2 if demand curve is assumed to be DD and to OP1 if demand curve is D1D1. However, output contracts more in the case of elastic demand (from OC to OC1). If demand is inelastic, output will shrink less (from OC to OC2).
“The general rule is that where demand is elastic, a change in supply will cause the quantity sold to change rather than price; where demand is inelastic, price changes rather than the quantity sold. Thus, trade union will find it more difficult to obtain a wage increase for its members without creating unemployment where the elasticity of demand for the product made is high.” (Jack Harvey)
(c) Policy Determination:
The concept of elasticity of demand is of great importance to a finance minister. While imposing tax or raising the existing tax rates, the finance minister must have sufficient knowledge of the elasticity of demand for the taxed commodity.
If the demand for the product is inelastic, the purpose of the tax—say revenue-earning—will be served. That is why taxes are mostly imposed or rates of taxes are raised in the case of commodities having inelastic demand.
Again, the concept may be used in the determination of incidence of a tax. It is easier to shift the burden of taxes on to the consumers if the product demand is assumed to be inelastic. Further, whether exportable or importable be taxed or not, the concept of elasticity may be of great use.
(d) Exchange Rate Determination:
In international trade too, the concept may be employed. For instance, as far as exchange rate (i.e., the rate at which one currency is exchanged for another currency) determination is concerned, the concept of elasticity of demand is of great importance.
The concept of elasticity of demand is used to justify whether devaluation of a currency is a right step in curbing balance of payment problems of a country. Devaluation is expected to correct the balance of payments disequilibrium if the sum of the elasticities of demand for export and import exceeds unity.
In international trade theory, within the limits set by the comparative costs, the terms of trade also depends on the elasticity of demand of each country for the goods of other countries.
In fine, elasticity of demand is a concept which has much applicability as far as business decision-making is concerned and is, therefore, of much importance in modern economics. In fact, most businessmen should try to form as precise an idea of elasticity as possible.
The concept of elasticity of demand is useful in business decision-making because “it is a convenient shorthand way of expressing the effects of price change on demand for a commodity and as such it is relevant to price fixing.”