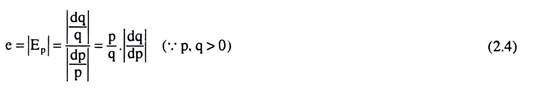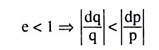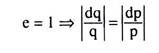In this article we will discuss about Marshall’s total outlay method for calculating the elasticity of demand.
Owing to the law of demand, the coefficient of price-elasticity of demand (Ep) is negative (Ep < 0). However, by price-elasticity of demand, it generally mean the numerical value of Ep.
If the numerical value of Ep is denoted by e, then it will be written as:
At any particular point on the demand curve for a good, e tells what would be the p.c. increase (or decrease) in quantity demanded if the price of the good decreases (or increases) by 1 per cent.
ADVERTISEMENTS:
If the proportionate or p.c. increase (or decrease) in quantity demanded (q) be greater than the proportionate or p.c. decrease (or increase) in price (p), i.e., if e > 1, then the demand for the good concerned is called the relatively elastic demand.
On the other hand, if the proportionate or p.c. increase (or decrease) in q be less than the proportionate or p.c. decrease (or increase) in p, then the demand for the good is called the relatively inelastic demand. And, if the proportionate or p.c. increase (or decrease) in q be equal to the proportionate or p.c. decrease (or increase) in p, then the demand for the good is called unitary elastic demand.
The implications of e being greater than, less than, or equal to 1.
ADVERTISEMENTS:
From the definition, it is obtained:
⇒ p.c. change in q > p.c. change in p
⇒ p.c. rise (or fall) in q > p.c. fall (or rise) in p
ADVERTISEMENTS:
⇒ if p falls (or rises), the total outlay (expenditure) of the buyers on the good would rise (or fall).
That is, the relation between the price of a good and the total outlay of its buyers would be inverse or negative if e > 1, or, demand is relatively elastic.
Again, by definition, it is obtained:
⇒ p.c. change in q < p.c. change in p
⇒ p.c. rise (or fall) in q < p.c. fall (or rise) in p
⇒ if p falls (or rises), the total outlay of the buyers would fall (or rise) That is, the relation between the price of a good and the total outlay of its buyers on the good would be direct or positive, if e < 1, or, demand is relatively inelastic.
Lastly, by definition, it is obtained:
⇒ p.c. change in q = p.c. change in p
ADVERTISEMENTS:
⇒ p.c. rise (or fall) in q = p.c. fall (or rise) in p
⇒ if p falls (or rises), the total outlay of the buyers would remain unchanged.
That is, the total outlay of the buyers of the good would be independent of the change in p, if e = 1, or, demand is unitary elastic.
ADVERTISEMENTS:
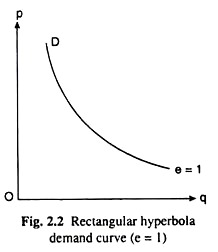
If e = 1, or, demand for the good is unitary elastic, total outlay of the buyers, or, p x q, would be a constant at each price.
In this case, the equation of the demand curve would be:
p x q = constant (2.5)
Since eq. (2.5) is that of a rectangular hyperbola, the demand curve in this case would be a rectangular hyperbola like the one given in Fig. 2.2.
ADVERTISEMENTS:
It is concluded that if, as a result of a fall (or rise) in the price of a good, the total outlay of the buyers increases (or decreases), then: e > 1. Again, if, as the price falls (or rises), the total outlay also falls (or rises), then, e < 1. Lastly, if, as price falls (or rises), the total outlay of the buyers remains constant, then, e = 1.
That is, by observing the relation between the price and the total outlay, to know whether demand is relatively elastic (e > 1), or relatively inelastic (e < 1) or unitary elastic (e = 1). This is Marshall’s total outlay method of elasticity measurement.