Consumer Behavior Analysis: Cardinal Utility Approach

The analysis of consumer behavior seeks to answer two questions.

Firstly, how does a consumer decide the optimum quantity of a good that he/she selects to consume?

Secondly, how the disposable income is allocated by the consumer for different goods, so that he/she maximizes the utility?

The cardinal utility approach answers these two questions on the basis of the following assumptions:

i. Rationality:

Assumes that a consumer is rational and satisfies his/her wants in order of his/her preferences. Therefore, he/she firstly prefers to purchase those goods which yield highest utility and lastly those that provide lowest utility.

ii. Limited Money Income:

Refers to one of the important assumptions of the cardinal utility approach. According to this approach, a consumer has a limited amount of income to be expended on goods selected by him/her for consumption. Therefore, in such a case when there is an objective of utility maximization along with limited income, he/she selects those goods whose consumption is unavoidable.

iii. Maximization of Satisfaction:

Implies that every rational consumer strives to maximize his/her satisfaction from the limited income.

iv. Utility is Measurable:

Assumes that utility is cardinally measureable. Therefore, utility of one unit of good equals to the units of money that a consumer is willing to pay, which means that 1 util = 1 unit of money.

v. Diminishing Marginal Utility:

Constitutes the basis for consumer behavior analysis. The utility gained falls as more and more units of a good are consumed.

vi. Constant Marginal Utility of Money:

Implies that whatever the level of income, the MU of money remains the same. According to this assumption, money is used as a measure of utility.

vii. Utility is Additive:

Implies that utility is not only cardinally measurable, but can be added together to obtain the total utility. For instance, a consumer consumes X₁, X₂, and X₃ units of good X and derives U₁, U₂ and U₃ utils, respectively.

In such a case, the total utility derived by a consumer from n units of good X is expressed as:

U_n = U₁ (X₁) + U₂ (X₂) + U₃ (X₃) +…………+ U_n (X_n)

Consumer’s Equilibrium through Utility:

A consumer is one who buys goods and services for his/her personal satisfaction. In theoretical terms, consumer’s equilibrium is achieved at a point when he/she reaches to the maximum level of his/her satisfaction, given resources and other conditions. On the other hand, in technical terms, a consumer reaches his maximum satisfaction level when the last unit of money spent on each good yields the same utility.

Let us take an example of one good to explain how a consumer reaches equilibrium.

Suppose a consumer consumes only one good X with a given income. He has two options either to spend income to purchase good X or retain it in the form of an asset. If the MU of good X (MUx) is greater than MU of money (MUm), the consumer would purchase the good.

Therefore, the consumer would spend his income on good X as long as utility of a good is greater than the price of a good, which implies MUx > Px (MUm). Here, the assumption is that MU of a good diminishes as more and more unit of the good is consumed and MU of money remains constant that is MUm=1.

Thus, consumer reaches equilibrium when:

MUx = Px(MUm)

Or

Mux/Px (MUm) = 1

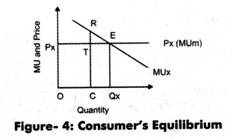
The consumer’s equilibrium is shown graphically in Figure-4:

As shown in Figure-4, the horizontal line Px shows the constant utility of money and MUx curve represents the diminishing marginal utility of a good. The intersection of MUx and Px curve takes place at E that is when quantity consumed is OQx, then MUx=Px(MUm).

Thus, consumer achieves equilibrium at E. Above point E, MUx > Px(MUm) implying that a consumer increase the consumption of good as utility achieved is more. At point R, consumer gains MU as RC where cost incurred is TC. Thus, marginal gain is RT and this situation exists till a consumer reaches point E.

If we look at the point below point E, where MUx < Px (MUm), a consumer would consume more than OQx and loses utility. Thus, satisfaction is increased by reducing the consumption. Therefore, point E is the equilibrium point.

In real life, a consumer consumes a large amount of goods, thus question arises how a consumer achieves equilibrium in case of a number of goods. A rational consumer consumes goods according to the preference. He/she would first purchase the good that yields the highest utility followed by the good yielding second highest utility. The expenditure is switched from one good to another till a stage is reached when MU of each good is same per unit of expenditure. This is called law of equi-marginal utility.

Let us discuss consumer equilibrium in case of two goods X and Y whose prices are Px and Py, respectively.

Consumer’s equilibrium is given as:

MUx=Px (MUm)

And MUy=Py(MUm)

The consumer’s equilibrium is expressed as:

MU_x/P_x(MU_x) = 1 = MU_y/P_y(MU_y)

It can be further rewritten as:

MU_x/P_x = MU_y/P_y

The aforementioned equation implies that a consumer reaches the equilibrium when MU derived from each rupees spent on two goods is same.

or

MU_x/MU_y = P_x/P_y

The aforementioned equation implies that a consumer is in equilibrium when MU ratio of any two goods equals the price ratio.

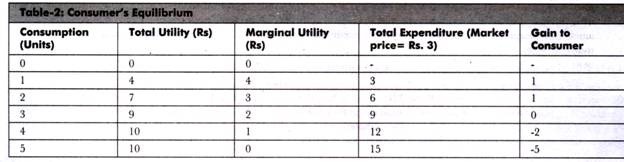
Let us now take the numerical example to learn consumer’s equilibrium with the help of Table-2:

From Table-2, it can be seen when a consumer buys one unit of a good at the market price of Rs. 3, he/she gains utility worth Rs. 4 In such a case, the consumer gains Re. 1. When he/she buys two units, the utility gained is Rs. 7 and total price paid is Rs 6. Again, he/she gains Re 1. Next, when he/she purchases three units, the utility gained is Rs. 9 and price paid is Rs. 9.

In such a case’ he/she does not gain anything. If he buys further, the total gain would become negative. From Table-2, it can be seen that MU is equal to price two units of consumption. Consumer equilibrium is achieved when the consumer buys two units because at this point quantity and utility gained is maximum and MU (Rs. 3) is equal to price (Rs. 3).

Derivation of Individual Demand:

The derivation of demand curve was done on the basis of the law of demand. It should be noted that the demand curve and law of demand are based on the utility maximizing behavior of consumers. The analysis of consumer equilibrium helps in deriving an individual demand curve for a good. As discussed earlier, consumer equilibrium takes place when MUx= Px (MUm).

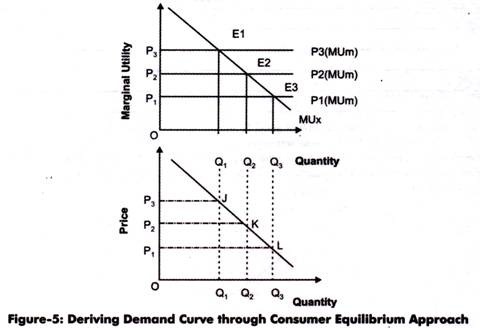
Figure-5 shows the derivation of demand curve from MUx:

Figure-5 shows the derivation of demand curve for good X. The price quantity combination corresponding to equilibrium points E1 E2 and E3 are shown at point J, K, and L, respectively which gives a demand curve for good X. Suppose E1 is the point of equilibrium at price P3 and quantity OQ1. If price falls to P2, the equilibrium would be disturbed and shift to E2 with quantity OQ2.

Similarly, when the price becomes P1, equilibrium shifts to E3 with quantity OQ3. Thus, when price increases, quantity demanded decreases. This inverse relationship between price and quantity gives the demand curve. Explaining with the help of utility, if P3 falls to P2, MUx > P3 (MUm) at OQ1. Thus, for maintaining equilibrium, the quantity demanded by a consumer should increase to OQ2, which would reduce MUx. Thus, equilibrium is achieved at MUx =P2 (MUm).