In this article we will discuss about the lexicographic orderings by consumers, explained with the help of suitable diagrams.
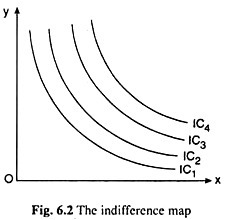
The indifference curves (ICs) would be negatively sloped, i.e., they would be sloping downward towards right like the curves given in Fig. 6.2. Axiom of continuity of preferences ensures that the ICs really exist.
However, a consumer may order his commodity combinations in such a way that would preclude the existence of ICs. Suppose that the consumer craves so much for a certain good, X, that he would prefer any combination that would have more of X, whatever may be the quantity of the other good, Y, in the bundle.
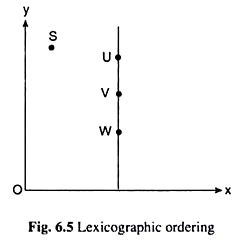
But if any two combinations contained equal amounts of X, then he would prefer the bundle with more of Y. This kind of ordering has been shown in Fig. 6.5.
ADVERTISEMENTS:
In this figure, all combinations to the right of V contain more of good X. Hence all points to y the right of V are preferred to V and all points to the left of V are inferior to V. Also, for the combinations with a given amount of good X as of point V, those lying to the north of V (like U), would be preferred to V, and those lying to the south of V (like W), would be inferior to the combination V.
Now consider another point like S. The consumer might have been indifferent between S and V by virtue of the MIB axiom. But here S would be definitely inferior to V because it lies to the left of V. In short, in the commodity space of Fig. 6.5 there are no points other than V itself which are indifferent to V.
Therefore, here the indifference curve does not exist. This kind of ordering is called a lexicographic or lexical ordering. It may be noted that in the lexicographic ordering, the axiom of continuity of preferences has been violated.