Consumer’s Behaviour: Cardinal Utility Analysis (Explained With Diagram)

From time to time, different theories have been advanced to explain consumer’s demand for a good and to derive a valid demand theorem.

Cardinal utility analysis is the oldest theory of demand which provides an explanation of consumer’s demand for a product and derives the law of demand which establishes an inverse relationship between price and quantity demanded of a product.

Introduction:

The price of a product depends upon the demand for and the supply of it. In this part of the book we are concerned with the theory of consumer’s behaviour, which explains his demand for a good and the factors determining it. Individual’s demand for a product depends upon price of the product, income of the individual, the prices of related goods.

It can be put in the following functional form:

D_x= f(P_x, I, P_y, P₂, T etc.)

where D_x stands for the demand of good X, P_x for price of good X, I for individual’s income, P_y P_z for the prices of related goods and T for tastes and preferences of the individual. But among these determinants of demand, economists single out price of the good in question as the most important factor governing the demand for it. Indeed, the function of a theory of consumer’s behaviour is to establish a relationship between quantity demanded of a good and its own price and to provide an explanation for it.

Recently, cardinal utility approach to the theory of demand has been subjected to severe criticisms and as a result some alternative theories, namely, Indifference Curve Analysis, Samuelson’s Revealed Preference Theory, and Hicks’ Logical Weak Ordering Theory have been propounded.

Assumptions of Cardinal Utility Analysis:

Cardinal utility analysis of demand is based upon certain important assumptions. Before explaining how cardinal utility analysis explains consumer’s equilibrium in regard to the demand for a good, it is essential to describe the basic assumptions on which the whole utility analysis rests. As we shall see later, cardinal utility analysis has been criticised because of its unrealistic assumptions.

The basic assumptions or premises of cardinal utility analysis are as follows:

The Cardinal Measurability of Utility:

The exponents of cardinal utility analysis regard utility to be a cardinal concept. In other words, they hold that utility is a measurable and quantifiable entity. According to them, a person can express utility or satisfaction he derives from the goods in the quantitative cardinal terms. Thus, a person can say that he derives utility equal to 10 units from the consumption of a unit of good A, and 20 units from the consumption of a unit of good B.

Moreover, the cardinal measurement of utility implies that a person can compare utilities derived from goods in respect of size, that is, how much one level of utility is greater than another. A person can say that the utility he gets from the consumption of one unit of good B is double the utility he obtains from the consumption of one unit of good A.

According to Marshall, marginal utility is actually measurable in terms of money. Money represents the general purchasing power and it can therefore be regarded as a command over alternative utility-yielding goods. Marshall argues that the amount of money which a person is prepared to pay for a unit of a good rather than go without it is a measure of the utility he derives from that good.

Thus, according to him, money is the measuring rod of utility Some economists belonging to the cardinalist school measure utility in imaginary units called “utils” They assume that a consumer is capable of saying that one apple provides him utility equal to 4 utils. Further, on this ground, he can say that he gets twice as much utility from an apple as compared to an orange.

The Hypothesis of Independent Utilities:

The second important tenet of the cardinal utility analysis is the hypothesis of independent utilities. On this hypothesis, the utility which a consumer derives from a good is the function of the quantity of that good and of that good only In other words, the utility which a consumer obtains from a good does not depend upon the quantity consumed of other goods; it depends upon the quantity purchased of that good alone.

On this assumption, then the total utility which a person gets from the whole collection of goods purchased by him is simply the total sum of the separate utilities of the goods. Thus, the cardinalist school regards utility as ‘additive’, that is, separate utilities of different goods can be added to obtain the total sum of the utilities of all goods purchased.

Constancy of the Marginal Utility of Money:

Another important assumption of the cardinal utility analysis is the constancy of the marginal utility of money. Thus, while the cardinal utility analysis assumes that marginal utilities of commodities diminish as more of them are purchased or consumed, but the marginal utility of money remains constant throughout when the individual is spending money on a good and due to which the amount of money with him varies. Daniel Bernoulli first of all introduced this assumption but later Marshall adopted this in his famous book “Principles of Economics’.

As stated above, Marshall measured marginal utilities in terms of money. But measurement of marginal utility of goods in terms of money is only possible if the marginal utility of money itself remains constant. It should be noted that the assumption of constant marginal utility of money is very crucial to the Marshallian analysis, because otherwise Marshall could not measure the marginal utilities of goods in terms of money. If money which is the unit of measurement itself varies as one is measuring with it, it cannot then yield correct measurement of the marginal utility of goods.

When price of a good falls and as a result the real income of the consumer rises, marginal utility of money to him will fall but Marshall ignored this and assumed that marginal utility of money did not change as a result of the change in price. Likewise, when price of a good rises the real income of the consumer will fall and his marginal utility of money will rise. But Marshall ignored this and assumed that marginal utility of money remains the same. Marshall defended this assumption on the ground that “his (the individual consumer’s) expenditure on any one thing is only a small part of his whole expenditure.”

Introspective Method:

Another important assumption of the cardinal utility analysis is the use of introspective method in judging the behaviour of marginal utility. “Introspection is the ability of the observer to reconstruct events which go on in the mind of another person with the help of self-observation. This form of comprehension may be just guesswork or intuition or the result of long lasting experience.”

Thus, the economists construct with the help of their own experience the trend of feeling which goes on in other men’s mind. From his own response to certain forces and by experience and observation one gains understanding of the way other people’s minds would work in similar situations. To sum up, in introspective method we attribute to another person what we know of our own mind. That is, by looking into ourselves we see inside the heads of other individuals.

So the law of diminishing marginal utility is based upon introspection. We know from our own mind that as we have more of a thing, the less utility we derive from an additional unit of it. We conclude from it that other individuals’ mind will work in a similar fashion, that is, marginal utility to them of a good will diminish as they have more units of it.

With the above basic premises, the founders of cardinal utility analysis have developed two laws which occupy an important place in economic theory and have several applications and uses.

These two laws are:

(1) Law of Diminishing Marginal Utility and

(2) Law of Equi-Marginal Utility.

It is with the help of these two laws about consumer’s behaviour that the exponents of cardinal utility analysis have derived the law of demand. We explain below these two laws in detail and how law of demand is derived from them.

Law of Diminishing Marginal Utility:

An important tenet of cardinal utility analysis relates to the behaviour of marginal utility. This familiar behaviour of marginal utility has been stated in the Law of Diminishing Marginal Utility according to which marginal utility of a good diminishes as an individual consumes more units of a good. In other words, as a consumer takes more units of a good, the extra utility or satisfaction that he derives from an extra unit of the good goes on falling.

It should be carefully noted that it is the marginal utility and not the total utility that declines with the increase in the consumption of a good. The law of diminishing marginal utility means that the total utility increases at a decreasing rate.

Marshall who has been a famous exponent of the cardinal utility analysis has stated the law of diminishing marginal utility as follows:

“The additional benefit which a person derives from a given increase of his stock of a thing diminishes with every increase in the stock that he already has.”

This law is based upon two important facts. First, while the total wants of a man are virtually unlimited, each single want is satiable. Therefore, as an individual consumes more and more units of a good, intensity of his want for the good goes on falling and a point is reached where the individual no longer wants any more units of the good. That is, when saturation point is reached, marginal utility of a good becomes zero. Zero marginal utility of a good implies that the individual has all that he wants of the good in question.

The second fact on which the law of diminishing marginal utility is based is that the different goods are not perfect substitutes for each other in the satisfaction of various wants. When an individual consumes more and more units of a good, the intensity of his particular want for the good diminishes but if the units of that good could be devoted to the satisfaction of other wants and yielded as much satisfaction as they did initially in the satisfaction of the first want, marginal utility of the good would not have diminished.

It is obvious from above that the law of diminishing marginal utility describes a familiar and fundamental tendency of human nature. This law has been arrived at by introspection and by observing how consumers behave.

Illustration of the Law of Diminishing Marginal Utility:

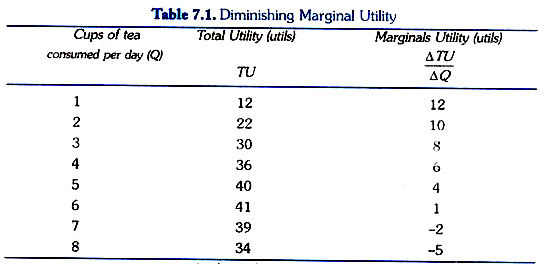
Consider Table 7 1 where we have presented the total and marginal utilities derived by a person from cups of tea consumed per day. When one cup of tea is taken per day the total utility derived by the person is 12 utils. And because this is the first cup its marginal utility is also 12 utils with the consumption of 2nd cup per day, the total utility rises to 22 utils but marginal utility falls to 10. It will be seen from the table that as the consumption of tea increases to six cups per day, marginal utility from the additional cup goes on diminishing (i.e. the total utility goes on increasing at a diminishing rate).

However, when the cups of tea consumed per day increases to seven, then instead of giving positive marginal utility, the seventh cup gives negative marginal utility equal to – 2 utils. This is because too many cups of tea consumed per day (say more than six for a particular individual) may cause acidity and gas trouble. Thus, the extra cups of tea beyond six to the individual in question gives him disutility rather than positive satisfaction.

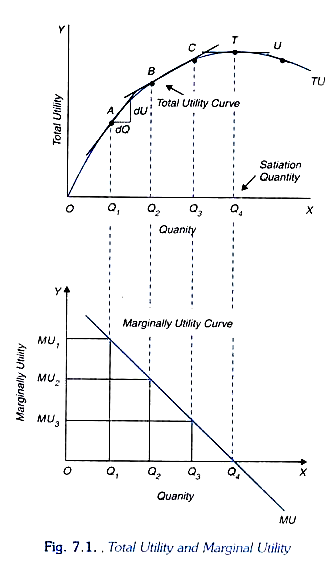
Figure 7 1 illustrates the total utility and the marginal utility curves. The total utility curve drawn in Figure 7.1 is based upon three assumptions. First, as the quantity consumed per period by a consumer increases his total utility increases but at a decreasing rate. This implies that as the consumption per period of a commodity by the consumer increases, marginal utility diminishes as shown in the lower panel of Figure 7.1.
Secondly, as will be observed from the figure when the rate of consumption of a commodity per period increases to Q₄, the total utility of the consumer reaches its maximum level.

Therefore, the quantity Q₄ of the commodity is called satiation quantity or satiety point. Thirdly, the increase in the quantity consumed of the good per period by the consumer beyond the satiation point has an adverse effect on his total utility that is, his total utility declines if more than Q₄ quantity of the good is consumed.

This means beyond Q₄ marginal utility of the commodity for the consumer becomes negative ads will be seen from the lower panel of Figure 7.1 beyond the satiation point Q₄ marginal utility curve MU goes below the X-axis indicating it becomes negative beyond quantity Q₄ per period of the commodity consumed.

It is important to understand how we have drawn the marginal utility curve. As stated above marginal utility is the increase in total utility of the consumer caused by the consumption of an additional unit of the commodity per period. We can directly find out the marginal utility of the successive units of the commodity consumed by measuring the additional utility which a consumer obtains from successive units of the commodity and plotting them against their respective quantities.

However, in terms of calculus, marginal utility of a commodity X is the slope of the total utility function U = f(Q_x). Thus, we can derive the marginal utility curve by measuring the slope at various points of the total utility curve TU in the upper panel of Figure7.1 by drawing tangents at them. For instance, at the quantity Q₁ marginal utility (i.e. dU/ dQ = MU₁) is found out by drawing tangent at point A and measuring its slope which is then plotted against quantity in the lower panel of Figure 7.1. In the lower panel we measure marginal utility of the commodity on the Y-axis. Likewise, at quantity Q₂ marginal utility of the commodity has been obtained by measuring slope of the total utility curve TU at point B and plotting it in the lower panel against the quantity Q₂.

It will be seen from the figure that at Q₄ of the commodity consumed, the total utility reaches at the maximum level T. Therefore, at quantity Q₄ the slope of the total utility curve is zero at this point. Beyond the quantity Q₄ the total utility declines and marginal utility becomes negative. Thus, quantity Q₄ of the commodity represents the satiation quantity.

Another important relationship between total utility and marginal utility is worth noting. At any quantity of a commodity consumed the total utility is the sum of the marginal utilities. For example, if marginal utility of the first, second, and third units of the commodity consumed are 15, 12, and 8 units, the total utility obtained from these three units of consumption of the commodity must equals 35 units (15 + 12 + 8 = 35).

Similarly, in terms of graphs of total utility and marginal utility depicted in Figure 7.1 the total utility of the quantity Q₄ of the commodity consumed is the sum of the marginal utilities of the units of commodity up to point Q₄. That is, the entire area under the marginal utility curve MU in lower panel up to the point Q₄ is the sum of marginal utilities which must be equal to the total utility Q₄T in the upper panel.

Marginal Utility and Consumer’s Tastes and Preferences:

The utility people derive from consuming a particular commodity depends on their tastes and preferences. Some consumers like oranges, others prefer apples and still others prefer bananas for consumption. Therefore, the utility which different individuals get from these various fruits depends on their tastes and preferences.

An individual would have different marginal utility curves for different commodities depending on his tastes and preferences. Thus, utility which people derive from various goods reflect their tastes and preferences for them. However, it is worth noting that we cannot compare utility across consumers. Each consumer has a unique subjective utility scale. In the context of cardinal utility analysis, a change in consumer’s tastes and preferences means a shift in his one or more marginal utility curves.

However, it may be noted that a consumer’s tastes and preferences do not frequently change, as these are determined by his habits. Of course, tastes and preferences can change occasionally. Therefore, in economic theory we generally assume that tastes or preferences are given and relatively stable.

Significance of Diminishing Marginal Utility:

The significance of the diminishing marginal utility of a good for the theory of demand is that it helps us to show that the quantity demanded of a good increase as its price falls and vice versa. Thus, it is because of the diminishing marginal utility that the demand curve slopes downward. If properly understood the law of diminishing marginal utility applies to all objects of desire including money.

But it is worth mentioning that marginal utility of money is generally never zero or negative. Money represents purchasing power over all other goods, that is, a man can satisfy all his material wants if he possesses enough money. Since man’s total wants are practically unlimited, therefore, the marginal utility of money to him never falls to zero.

The marginal utility analysis has a good number of uses and applications in both economic theory and policy. The concept of marginal utility is of crucial significance in explaining determination of the prices of commodities. The discovery of the concept of marginal utility has helped us to explain the paradox of value which troubled Adam Smith in “The Wealth of Nations.”

Adam Smith was greatly surprised to know why water which is so very essential and useful to life has such a low price (indeed no price), while diamonds which are quite unnecessary, have such a high price. He could not resolve this water-diamond paradox. But modern economists can solve it with the aid of the concept of marginal utility.

According to the modern economists, the total utility of a commodity does not determine the price of a commodity and it is the marginal utility which is crucially important determinant of price. Now, the water is available in abundant quantities so that its relative marginal utility is very low or even zero. Therefore, its price is low or zero. On the other hand, the diamonds are scarce and therefore their relative marginal utility is quite high and this is the reason why their prices are high.

Prof. Samuelson explains this paradox of value in the following words:

The more there is of a commodity, the less the relative desirability of its last little unit becomes, even though its total usefulness grows as we get more of the commodity. So, it is obvious why a large amount of water has a low price or why air is actually a free good despite its vast usefulness. The many later units pull down the market value of all units.

Besides, the Marshallian concept of consumer’s surplus is based on the principle of diminishing marginal utility.

Consumer’s Equilibrium: Principle of Equi-Marginal Utility:

Principle of equi-marginal utility occupies an important place in cardinal utility analysis. It is through this principle that consumer’s equilibrium is explained. A consumer has a given income which he has to spend on various goods he wants. Now, the question is how he would allocate his given money income among various goods, that is to say, what would be his equilibrium position in respect of the purchases of the various goods. It may be mentioned here that consumer is assumed to be ‘rational’, that is, he carefully calculates utilities and substitutes one good for another so as to maximise his utility or satisfaction.

Suppose there are only two goods X and Y on which a consumer has to spend a given income. The consumer’s behaviour will be governed by two factors first, the marginal utilities of the goods and secondly, the prices of two goods. Suppose the prices of the goods are given for the consumer.

The law of equi-marginal utility states that the consumer will distribute his money income between the goods in such a way that the utility derived from the last rupee spent on each good is equal. In other words, consumer is in equilibrium position when marginal utility of money expenditure on each good is the same. Now, the marginal utility of money expenditure on a good is equal to the marginal utility of a good divided by the price of the good. In symbols,

MU_m = MU_x / P_x

Where MU_m is marginal utility of money expenditure and MU_m is the marginal utility of X and P_x is the price of X. The law of equi-marginal utility can therefore be stated thus: the consumer will spend his money income on different goods in such a way that marginal utility of money expenditure on each good is equal. That is, consumer is in equilibrium in respect of the purchases of two goods X and V when

MU_x / P_x= MU_y / P_y

Now, if MU_x / P_x and MU_y / P_y are not equal and MU_x / P_x is greater than MU_y / P_y, then the consumer will substitute good X for good Y. As a result of this substitution, the marginal utility of good X will fall and marginal utility of good y will rise. The consumer will continue substituting good X for good Y until MU_x / P_x becomes equal to MU_y / P_y. When MU_x / P_x becomes equal to MU_y / P_y the consumer will be in equilibrium.

But the equality of MU_x / P_x with MU_y / P_y can be achieved not only at one level but at different levels of expenditure. The question is how far does a consumer go in purchasing the goods he wants. This is determined by the size of his money income. With a given income and money expenditure a rupee has a certain utility for him: this utility is the marginal utility of money to him.

Since the law of diminishing marginal utility applies to money income also, the greater the size of his money income the smaller the marginal utility of money to him. Now, the consumer will go on purchasing goods until the marginal utility of money expenditure on each good becomes equal to the marginal utility of money to him.

Thus, the consumer will be in equilibrium when the following equation holds good:

MU_x / P_x = MU_y / P_y = MU_m

Where MU_m is marginal utility of money expenditure (that is, the utility of the last rupee spent on each good).

If there are more than two goods on which the consumer is spending his income, the above equation must hold good for all of them. Thus

MU_x / P_x = MU_y / P_y = …….. = MU_m

Let us illustrate the law of equi-marginal utility with the aid of an arithmetical table given below:

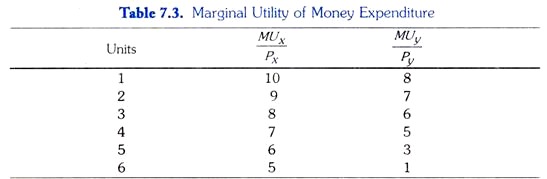
Let the prices of goods X and Y be Rs. 2 and Rs. 3 respectively. Reconstructing the above table by dividing marginal utilities (MU) of X by Rs. 2 and marginal utilities (MU) of 7 by Rs. 3 we get the Table 7.3.

Suppose a consumer has money income of Rs. 24 to spend on the two goods. It is worth noting that in order to maximise his utility the consumer will not equate marginal utilities of the goods because prices of the two goods are different. He will equate the marginal utility of the last rupee (i.e. marginal utility of money expenditure) spent on these two goods.

In other words, he will equate MU_x / P_x with MU_y / P_y while spending his given money income on the two goods. By looking at the Table 7.3 it will become clear that MU_x / P_x is equal to 5 utils when the consumer purchases 6 units of good X and MU_y / P_y is equal to 5 utils when he buys 4 units of good Y. Therefore, consumer will be in equilibrium when he is buying 6 units of good X and 4 units of good 7and will be spending (Rs. 2 x 6 + Rs. 3 x 4 ) = Rs. 24 on them that are equal to consumer’s given income. Thus, in the equilibrium position where the consumer maximises his utility.

MU_x / P_x = MU_y / P_y = MU_m

10/2 = 15/3 =5

Thus, marginal utility of the last rupee spent on each of the two goods he purchases is the same, that is, 5 utils.

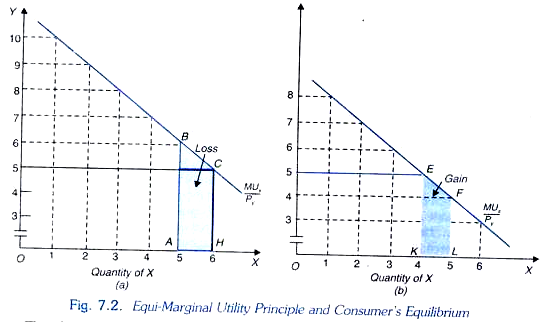
Consumers’ equilibrium is graphically portrayed in Fig. 7.2. Since marginal utility curves of goods slope downward, curves depicting and MU_x / P_x and MU_y / P_y also slope downward. Thus, when the consumer is buying OH of X and OK of Y, then

MU_x / P_x = MU_y / P_y = MU_m

Therefore, the consumer is in equilibrium when he is buying 6 units of X and 4 units of Y. No other allocation of money expenditure will yield him greater utility than when he is buying 6 units of commodity X and 4 units of commodity Y. Suppose the consumer buys one unit less of good X and one unit more of good Y.

This will lead to the decrease in his total utility. It will be observed from Figure 7.2 (a) that the consumption of 5 units instead of 6 units of commodity X means a loss in satisfaction equal to the shaded area ABCH and from Fig. 7.2(b) it will be seen that consumption of 5 units of commodity Y instead of 4 units will mean gain in utility equal to the shaded area KEFL. It will be noticed that with this rearrangement of purchases of the two goods, the loss in utility ABCH exceeds gain in utility KEFL.

Thus, his total satisfaction will fall as a result of this rearrangement of purchases. Therefore, when the consumer is making purchases by spending his given income in such a way that MU_x / P_x = MU_y / P_y , he will not like to make any further changes in the basket of goods and will therefore be in equilibrium situation by maximizing his utility.

Limitations of the Law of Equi-Marginal Utility:

Like other laws of economics, law of equi-marginal utility is also subject to various limitations. This law, like other laws of economics, brings out an important tendency among the people. This is not necessary that all people exactly follow this law in the allocation of their money income and therefore all may not obtain maximum satisfaction.

This is due to the following reasons:

(1) For applying this law of equi-marginal utility in the real life, consumer must weigh in his mind the marginal utilities of different commodities. For this he has to calculate and compare the marginal utilities obtained from different commodities.

But it has been pointed out that the ordinary consumers are not so rational and calculating. Consumers are generally governed by habits and customs. Because of their habits and customs they spend particular amounts of money on different commodities, regardless of whether the particular allocation maximises their satisfaction or not.

(2) For applying this law in actual life and equate the marginal utility of the last rupee spent on different commodities, the consumers must be able to measure the marginal utilities of different commodities in cardinal terms. However, this is easier said than done. It has been said that it is not possible for the consumer to measure utility cardinally.

Being a state of psychological feeling and also there being no objective units with which to measure utility, it is cardinally immeasurable. It is because of the immeasurability of utility in cardinal terms that the consumer’s behaviour has beenexplained with the help of ordinal utility by J.R. Hicks and R.G.D. Allen.

(3) Another limitation of the law of equi-marginal utility is found in case of indivisibility of certain goods. Goods are often available in large indivisible units. Because the goods are indivisible, it is not possible to equate the marginal utility of money spent on them. For instance, in allocating money between the purchase of car and foodgrains, marginal utilities of the last rupee spent on them cannot be equated.

An ordinary car costs about Rs. 300,000 and is indivisible, whereas foodgrains are divisible and money spent on them can be easily varied. Therefore, the marginal utility of rupee obtained from cars cannot be equalised with that obtained from foodgrains. Thus, indivisibility of certain goods is a great obstacle in the way of equalisation of marginal utility of a rupee from different commodities.

Derivation of Demand Curve and the Law of Demand:

We now turn to explain how the demand curve and law of demand is derived in the marginal utility analysis. As stated above, the demand curve or law of demand shows the relationship between price of a good and its quantity demanded. Marshall derived the demand curves for goods from their utility functions.

It should be further noted that in his utility analysis of demand Marshall assumed the utility functions of different goods to be independent of each other. In other words, Marshallian technique of deriving demand curves for goods from their utility functions rests on the hypothesis of additive utility functions, that is, utility function of each good consumed by a consumer does not depend on the quantity consumed of any other good.

As has already been noted, in case of independent utilities or additive utility functions, the relations of substitution and Complementarity between goods are ruled out. Further, in deriving demand curve or law of demand Marshall assumes the marginal utility of money expenditure (Mu_m) in general to remain constant.

We now proceed to derive demand curve from the law of equi-marginal utility. Consider the case of a consumer who has a certain given income to spend on a number of goods. According to the law of equi-marginal utility, the consumer is in equilibrium in regard to his purchases of various goods when marginal utilities of the goods are proportional to their prices.

Thus, the consumer is in equilibrium when he is buying the quantities of the two goods in such a way that satisfies the following proportionality rule:

MU_x / P_x = MU_y / P_y = MU_m

Where MU_m stands for marginal utility of money income in general.

With a certain given income for money expenditure the consumer would have a certain marginal utility of money (Mu_m) in general. In order to attain the equilibrium position, according to the above proportionality rule, the consumer will equalise his marginal utility of money (expenditure) with the ratio of the marginal utility and the price of each commodity he buys.

It follows therefore that a rational consumer will equalise the marginal utility of money (MU_m) with MU_x / P_x of good X, with MU_m/ P_Y of good 7 and so on. Given Ceteris Paribus assumption, suppose price of good X falls. With the fall in the price of good X, the price of good Y, consumer’s income and tastes remaining unchanged, the equality of the MU_x / P_x with MU_y / P_y and MU_m in general would be disturbed.

With the lower price than before MU_x / P_x will be greater than MU_y / P_y or MU_m (It is assumed of course that the marginal utility of money does not change as a result of the change in the price of one good). Then, in order to restore the equality, marginal utility of X or MU_x must be reduced. And the marginal utility of X or MU_x can be reduced only by the consumer buying more of the good X.

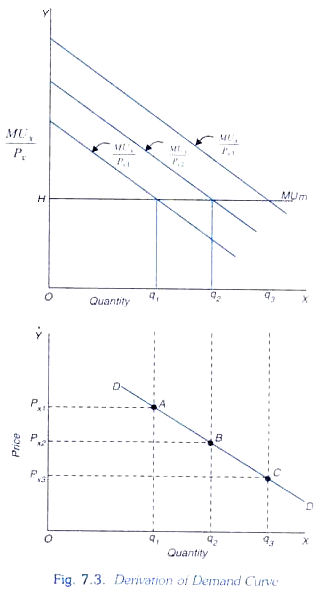
It is thus clear from the proportionality rule that as the price of a good falls, its quantity demanded will rise, other things remaining the same. This will make the demand curve for a good downward sloping. How the quantity purchased of a good increases with the fall in its price and also how the demand curve is derived in the cardinal utility analysis is illustrated in Fig. 7.3.

In the upper portion of Fig. 7.3, on the Y-axis MU_x / P_x is shown and on the X-axis the quantity demanded of good X is shown. Given a certain income of the consumer, marginal utility of money in general for him is equal to OH. The consumer is buying Oq₁ of good X when price is P_x1 since at the quantity Oq₁ of X, marginal utility of money OH is equal to MU_x / P_x1.

Now, when price of good X falls to P_x2. The curve will shift upward to the new position MU_x/P_x2. In order to equate marginal utility of money (OH) with the new MU_x / P_x2 the consumer increases the quantity demanded to Oq₂. Thus, with the fall in price of good X to P_x2, the consumer buys more of it.

It should be noted that no account is taken of the increase in real income of the consumer as a result of fall in price of good X. This is because if change in real income is taken into account, then marginal utility of money will also change and this would have an effect on the purchases of goods. Marginal utility of money can remain constant in two cases. First, when the elasticity of marginal utility curve (price elasticity of demand) is unity so that even with increase in the purchase of a commodity following the fall in price, the money expenditure made on it remains the same.

Second, marginal utility of money will remain approximately constant for small changes in price of unimportant goods, that is, goods which account for negligible part of consumer’s budget. In case of these unimportant goods increase in real income following the fall in price is negligible and therefore can be ignored.

At the bottom of Figure 7.3 the demand curve for X is derived. In this lower panel, price is measured on the Y-axis. As in the upper panel, the X-axis represents quantity. When the price of good X is Px₁, the relevant curve of MU/P is MU_x / P_x1 which is shown in the upper panel. With MU_x / P_x1, he buys Oq₁ of good X. Now, in the lower panel this quantity Oq₁ is directly shown to be demanded at the price Px₂.

When price of X falls to Px₂, the curve of MU/P shifts upward to the new position MU_x / P_x2. With MU_x / P_x2 the consumer buys Oq₂ of X. This quantity Oq₂ is directly shown to be demanded at price Px₂ lower panel. Similarly, by varying price further we can know the quantity demanded at other prices. Thus, by joining points A, B and C we obtain the demand curve DD. The demand curve DD slopes downward which shows that as price of a good falls, its quantity purchased rises.

Critical Evaluation of Marshall’s Cardinal Utility Analysis:

Cardinal utility analysis of demand which we have studied above has been criticised on various grounds.

The following shortcomings and drawbacks of cardinal utility analysis have been pointed out:

(1) Cardinal measurability of utility is unrealistic:

Cardinal utility analysis of demand is based on the assumption that utility can be measured in absolute, objective and quantitative terms. In other words, it is assumed in this analysis that utility is cardinally measurable. According to this, how much utility a consumer obtains from goods can be expressed or stated in cardinal numbers such as 1, 2, 3, 4 and so forth. But in actual practice utility cannot be measured in such quantitative or cardinal terms.

Since utility is a psychic feeling and a subjective thing, it cannot be measured in quantitative terms. In real life, consumers are only able to compare the satisfactions derived from various goods or various combinations of the goods. In other words, in the real life consumer can state only whether a good or a combination of goods gives him more or less, or equal satisfaction as compared to another. Thus, economists like J.R. Hicks are of the opinion that the assumption of cardinal measurability of utility is unrealistic and therefore it should be given up.

(2) Hypothesis of independent utilities is wrong:

Utility analysis also assumes that utilities derived from various goods are independent. This means that the utility which a consumer derives from a good is the function of the quantity of that good and of that good alone. In other words, the assumption of independent utilities implies that the utility which a consumer obtains from a good does not depend upon the quantity consumed of other goods; it depends upon the quantity purchased of that good alone.

On this assumption, the total utility which a person gets from the whole collection of goods purchased by him is simply the total sum of the separate utilities of various goods. In other words, utility functions are additive.

Neo-classical economists such as Jevons, Menger, Walras and Marshall considered that utility functions were additive. But in the real life this is not so. In actual life the utility or satisfaction derived from a good depends upon the availability of some other goods which may be either substitutes for or complementary with each other. For example, the utility derived from a pen depends upon whether ink is available or not.

On the contrary, if you have only tea, then the utility derived from it would be greater but if along with tea you also have the coffee, then the utility of tea to you would be comparatively less. Whereas pen and ink are complements with each other, tea and coffee are substitutes for each other.

It is thus clear that various goods are related to each other in the sense that some are complements with each other and some are substitutes for each other. As a result of this, the utilities derived from various goods are interdependent, that is, they depend upon each other. Therefore, the utility obtained from a good is not the function of its quantity alone but also depends upon the existence or consumption of other related goods (complements or substitutes).

It is thus evident that the assumption of the independence of utilities by Marshall and other supporters of marginal utility analysis is a great defect and shortcoming of their analysis. As we shall see below, the hypothesis of independent utilities along with the assumption of constant marginal utility of money reduces the validity of Marshallian demand theorem to the one- commodity model only.

(3) Assumption of constant marginal utility of money is not valid:

An important assumption of cardinal utility analysis is that when a consumer spends varying amount on a good or various goods or when the price of a good changes, marginal utility of money remains unchanged. But in actual practice this is not correct. As a consumer spends his money income on the goods, money income left with him declines.

With the decline in money income of the consumer as a result of increase in his expenditure on goods, the marginal utility of money to him rises. Further, when price of a commodity changes, the real income of the consumer also changes. With this change in real income, marginal utility of money will change and this would have an effect on the demand for the good in question, even though the total money income available with the consumer remains the same.

But utility analysis ignores all this and does not take cognizance of the changes in real income and its effect on demand for goods following the change in price of a good. As we shall see below, it is because of the assumption of constant marginal utility of money that Marshall ignored the income effect of the price change which prevented Marshall from understanding the composite character of the price effect (that is, price effect is the sum of substitution effect and income effect).

Moreover, as we shall see later, the assumption of constant marginal utility of money together with the hypothesis of independent utilities renders the Marshall’s demand theorem to be valid in case of one commodity. Further, it is because of the constant marginal utility of money and therefore the neglect of the income effect by Marshall that he could not explain Giffen Paradox.

According to Marshall, utility from a good can be measured in terms of money (that is, how much money a consumer is prepared to sacrifice for a good). But, to be able to measure utility in terms of money marginal utility of money itself should remain constant. Therefore, assumption of constant marginal utility of money is very crucial to Marshallian demand analysis. On the basis of constant marginal utility of money Marshall could assert that “utility is not only measurable in principle” but also “measurable in fact”.

But, as we shall see below, in case a consumer has to spread his money income on a number of goods, there is a necessity for revision of marginal utility of money with every change in price of a good. In other words, in a multi-commodity model marginal utility of money does not remain invariant or constant.

Now, when it is realised that marginal utility of money does not remain constant, then Marshall’s belief that utility is ‘measurable in fact’ in terms of money does not hold good. However, if in marginal utility analysis, utility is conceived only to be ‘measurable in principle’ and not in fact, then it practically gives up cardinal measurement of utility and comes near to the ordinal measurement of utility.

(4) Marshallian demand therem cannot genuinely be derived except in a one commodity case:

J.R. Hicks and Tapas Majumdar have criticised Marshallian utility analysis on the ground that “Marshallian demand theorem cannot genuinely be derived from the marginal utility hypothesis except in a one-commodity model without contradicting the assumption of constant marginal utility of money. In other words, Marshall’s demand theorem and constant marginal utility of money are incompatible except in a one commodity case. As a result, Marshall’s demand theorem cannot be validity derived in the case when a consumer spends his money on more than one good.

In order to know the truth of this assertion consider a consumer who has a given amount of money income to spend on some goods with given prices? According to utility analysis, the consumer will be in equilibrium when he is spending money on goods in such a way that the marginal utility of each good is proportional to its price. Let us assume that, in his equilibrium position, consumer is buying q₁ quantity of a good X at a price P₁. Marginal utility of good X, in his equilibrium position, will be equal to its price p₁ multiplied by the marginal utility of money (which, in Marshallian utility analisis, serves as the unit of measurement).

Thus, in the equilibrium position, the following equation will be fulfilled:

MU_x / = MU_m x p₁

Since the consumer is buying q₁ quantity of good X at price P₁, he will be spending P₁Q₁ amount of money on it. Now, suppose that the price of good X rises from p₁ to p₂. With this rise in price of X, all other things remaining the same, the consumer will at once find himself in disequilibrium state, for the marginal of good X will now be less than the higher price pg multiplied by the marginal utility of money (Mu_m) which is assumed to remain unchanged and constant. Thus, now there will be

MU_x < MU_m. P₂

In order to restore his equilibrium, the consumer will buy less of good X so that the marginal utility of good X (MUx) would rise and become equal to the product of p₂ and MU_m. Suppose in this new equilibrium position, he is buying q₂ of good X which will be less than q₁. With this he will now be spending p₂q₂ amount of money on good X. Now the important thing to see is that whether his new expenditure p₂q₂ on good X is equal to, smaller or greater than P₁ q₁.

This depends upon the elasticity of marginal utility curve i.e., price elasticity of demand. If the elasticity of marginal utility curve of good X is unity, then the new expenditure on good X (i.e. p₂q₂) after the rise in its price from p₁ to p₂ will be equal to the initial expenditure p₁q₁. When the monetary expenditure made on the good remains constant as a result of change in price, then the Marshallian theory is valid.

But constant monetary expenditure following a price change is only a rare phenomenon. However, the Marshallian demand theory breaks down when the new expenditure p₂q₂ after the rise in price, instead of being equal is smaller or greater than the initial expenditure p₂q₂.

If elasticity of marginal utility curve is greater than one (that is, price demand for the good is elastic), then the new expenditure p₂q₂, after the rise in price from p₁ to p₂, will be less than the initial expenditure p. On the other hand, if the elasticity of marginal utility curve is less than unity, then the new expenditure p₂q₂ after the rise in price will be greater than the initial expenditure p₁q₁.

Now, if the new expenditure p₂q₂ on good X is less than the initial expenditure p₁q₁ or it, it means more money will be left with the consumer to spend on goods other than X. And if the new expenditure p₂q₂ on good X is greater than the initial expenditure p₁q₁ on it, then less money would be left with him to spend on goods other than X.

In order that the consumer spends the entire amount of money available with him, then in case of new expenditure p₂q₂ on good X being smaller or greater than initial expenditure p₁q₁ on it, the expenditure or goods other than X and therefore consumer’s demand for them will change.

But in Marshallian theoretical framework, this further adjustment in consumer’s expenditure on goods other than X can occur only if the unit of utility measurement, that is, the marginal utility of money revised or changed. But Marshall assumes marginal utility of money to remain constant.

Thus, we see that marginal utility of money cannot be assumed to remain constant when the consumer has to spread his money income on a number of goods. In case of more than one good, Marshallian demand theorem cannot be genuinely derived while keeping the marginal utility of money constant.

If, in Marshallian demand analysis, this difficulty is avoided “ by giving up the assumption of constant marginal utility of money, then money can no longer provide the measuring rod, and we can no longer express the marginal utility of a commodity in units of money. If we cannot express marginal utility in terms of common numeraire (which money is defined to be) the cardinality of utility would be devoid of any operational significance.

Only in case there is one good on which the consumer has to spend his money, Marshallian demand theorem can be validity derived. To conclude, in the words of Majumdar, “Except in a strictly one-commodity world, therefore, the assumption of a constant marginal utility of money would be incompatible with the Marshallian demand theorem.

Without the assumption of an invariant unit of measurement, the assertion of measurability would be entirely meaningless. The necessity and the possibility of revision of the unit of utility measurement, following every change in price, had been assumed away in Marshallian theory under the cover of ‘other things remaining the same’ clause.”

(6) Cardinal utility analysis does not split up the price affect into substitution and income effects: The third shortcoming of the cardinal utility analysis is that it does not distinguish between the income effect and the substitutional effect of the price change.

We know that when the price of a good falls, the consumer becomes better off than before, that is, a fall in price of a good brings about an increase in the real income of the consumer. In other words, if with the fall in price the consumer purchases the same quantity of the good as before, then he would be left with some income.

With this income he would be in a position to purchase more of this good as well as other goods. This is the income effect of the fall in price on the quantity demanded of a good. Besides, when the price of a good falls, it becomes relatively cheaper than other goods and as a result the consumer is induced to substitute that good for others. This results is increase in quantity demanded of that good. This is the substitution effect of the price change on the quantity demanded of the good.

With the fall in price of a good, the quantity demanded of it rises because of income effect and substitution effect. But cardinal utility analysis does not make clear the distinction between the income and the substitution effects of the price change. In fact, Marshall and other exponents of marginal utility analysis ignored income effect of the price change by assuming the constancy of marginal utility of money. Thus, according to Tapas Majumdar, “the assumption of constant marginal utility of money obscured Marshall’s insight into the truly composite character of the unduly simplified price-demand relationship”.

They explained the changes in demand as a result of change in the price of a good on the basis of substitution effect on it. Thus, marginal utility analysis does not tell us about how much quantity demanded increases due to income effect and how much due to substitution effect as a result of the fall in price of a good J R Hicks rightly remarks, “that distinction between income effect and substitution effect of a price change is accordingly left by the cardinal theory as an empty box which is crying out to be filled. In the same way, Tapas Majumdar says, “The efficiency and precision with which the Hicks-Allen approach can distinguish between the income and subsitutuion effects of a price change really leaves the cardinal argument in a very poor state indeed.

(7) Marshall could not explain Giffen Paradox:

By not visualizing the price effect as a combination of substitution and income effects and ignoring the income effect of the price change, Marshall could not explain the Giffen Paradox. He treated it merely as an exception to his law of demand. In contrast to it, indifference curve analysis has been able to explain satisfactorily the Giffen good case.

According to indifference curve analysis, in case of a Giffen Paradox or the Giffen good negative income effect of the price change is more powerful than substitution effect so that when the price of a Giffen good falls the negative income effect outweighs the substitution effect with the result that quantity demanded of it falls.

Thus in case of a Giffen good, quantity demanded varies directly with the price and the Marshall’s law of demand does not hold good. It is because of the constant marginal utility of money and therefore the neglect of the income effect of price change that Marshall could not explain why the quantity demanded of the Giffen good falls when its price falls and rises when its price rises. This is a serious lacuna in Marshalllian’s utility analysis of demand.

(8) Marginal utility analysis assumes too much and explains too little:

Marginal utility analysis is also criticised on the ground that it takes more assumptions and also more severe ones than those of ordinal utility analysis of indifference curve technique Marginal utility analysis assumes, among others, that utility is cardinally measurable and also that marginal utility of money remains constant. Hicks-Allen’s indifference curve analysis does not take these assumptions and even then it is not only able to deduce all the theorems which cardinal utility analysis can but also deduces a more general theorem of demand.

In other words, indifference curve analysis explains not only that much as cardinal utility analysis does but even goes further and that too with fewer and less severe assumptions. Taking less severe assumption of ordinal utility and without assuming constant marginal utility of money, analysis is able to arrive at the condition of consumer’s equilibrium, namely, equality o marginal rate of substitution (MRS) with the price ratio between the goods, which is similar to the proportionality rule of Marshall. Further, since indifference curve analysis does not assume constant marginal utility of money, it is able to derive a valid demand theorem in a more than one commodity case.

In other words indifference curve analysis dearly explains why in case o Giffen goods quality demanded increases with the rise in price and decreases with the fall in price. Indifference curve analysis explains even the case of ordinary inferior goods (other than Giffen goods) in a more analytical Inner.

It may be noted that even if the valid demand f derived for the Marshallian hypothesis, it would still be rejected because “better hypothesis” of indifference preference analysis was available which can enunciate more general demand theorem (covering the case of Giffen goods) with fewer, less severe and more realistic assumptions.

Because of the above drawbacks, cardinal utility analysis has been given up in modern economic theory and demand is analysed with new approaches to demand theory.