Let us learn about the the budget constraint of a consumer.
A consumer always tries to maximize his satisfaction. But, in this pursuit, he is hampered by his limited money income, i.e., budget. A budget line is defined as the purchasable combinations of two goods, given the prices of each good and consumer’s income. Thus the budget constraint describes the different amount of two commodities that a consumer can afford.
Assume that a consumer has a fixed money income, M, to purchase two goods, X and Y whose prices are PX and PY, respectively. Also assume that PX and PY are fixed.
Thus, the total expenditure on X and Y can be represented as:
ADVERTISEMENTS:
M = PX.X + PY.Y
This is the equation of a straight line. Dividing the budget line equation by PY we obtain
M/PY = PX. X/PY+ Y
Subtracting PX. X/PY from both sides of this equation we obtain the value of Y
ADVERTISEMENTS:
Y = M/PY – PX. X/PY
Similarly, solving for X, we get
X = M/PX – PY. Y/PX
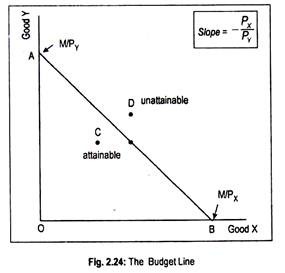
Here M/PY is the vertical intercept of the equation. It shows the maximum purchasable amount of Y, if no unit of X is bought. This is represented by the distance OA in Fig. 2.24. Similarly M/PX is the horizontal intercept. It shows the maximum purchasable amount of X, if no Y is bought. This is represented by OB.
Thus, A and B are the two extreme points. By joining these two points we obtain the budget line AB that shows purchasable combinations of goods X and Y where the whole of income is spent. Thus, AB is a straight downward sloping line. The consumer cannot go beyond the line AB since money income will not permit him to do so (point D).
Thus, the budget constraint describes the different bundles of two goods that a consumer can buy. It is to be noted here that as long as the prices of two goods are fixed and independent of the quantities purchased, the budget line is, necessarily, linear.
Since the line AB has a negative slope, its slope is represented by the price ratio of goods X and Y:
= – amount of Y/(+) amount of X = (M/PY)/(M/PX)
Slope = – OA/OB = – PX/PY
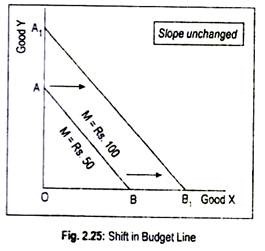
The position and slope of the budget line depends on money income and the prices of two goods. In other words, if there is a change in money income or a change in the price of any good, there will be a shift in the budget line.
Suppose, only money income is doubled. Now the budget line equation will be
2M = X.PX + Y.PY
This results in an upward shifting of the budget line. Prior to the increase in money income, budget line was AB in Fig. 2.25. After the increase in money income, new budget line becomes A1B1. As there is a parallel shift of the budget line, its slope remains unchanged.
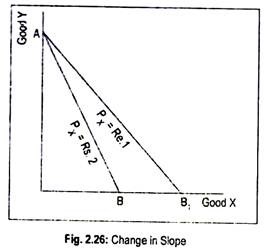
Let us assume that the price of X falls. In Fig. 2.26, AB is the initial budget line. Its slope is PX/PY. Now, if price of X falls from Rs. 2 to Re. 1, the budget line shifts to AB,. Since the line AB is steeper than AB1, the slope of the budget line AB (PX/PY) is greater than the slope of the budget line AB1 (PX1/PY).