Theory of Production and the Production Function

Let us make an in-depth study of the theory of production and the production function in economics.

“Knowledge is the only instrument of pro­duction that is not subject to diminishing returns – J. M. Clark, 1957.”

Subject Matter:

A firm’s objective is profit maximisation. If, in the short run, its total output remains fixed (due to capacity constraints) and if it is a price-taker (i.e., cannot fix the price or change price on its own as in a purely competitive market) its total revenue will also remain fixed. Therefore, the only way to maximise profit is to minimise cost. Thus profit maximisation and cost minimisation are the two sides of the same coin.

Moreover, supply depends on cost of production. The decision to supply an extra unit depends on the marginal cost of producing that unit. Perhaps the most important determinant of the firm’s price- output decision in any market is its cost of production.

The firm’s cost, in its turn, depends on two main factors:

(1) the technical relation between inputs and output (i.e., how outputs vary as inputs vary), and

(2) factors price’s (i.e., the price of labour or the wage, the price of capital or the interest rate, etc.). In this article we will discuss a new concept, called production function. In this context we will clear a distinction between the short-run and the long- run as also between the return to a factor and the return to scale.

The business firm is a technical unit in which inputs are converted into output for sale to consumers, other business firms and various government departments. In the theory of production we are concerned with the nature of the conversion process, i.e., how inputs are converted into output. The key concept in the theory of production is the production function.

The Production Function:

The production function shows the relation between input changes and output changes. It also shows the maximum amount of output that can be obtained by the firm from a fixed quantity of resources.

The production function is expressed as:

Q = f (K, L, etc.)

Where Q is output (which is the dependent variable) and K and L are capital and labour inputs, respectively. We can think of other inputs as well, such as land. For the sake of convenience we assume here that the firm employs only two factors of production— labour and capital. The firm’s output is treated as a flow, i.e., so many units per period of time. The volume of output of the firm’s product, per period of time, depends on the quantities of these factors that are used by the firm.

Let us now suppose that the firm wishes to increase its volume (rate) of output. This can be achieved by increasing the inputs of one or both factors of production. However, it is very easy to vary the quantity of labour in the production process. It can be done very quickly (in a week or a month). On the other hand, a fairly long period of time is required to vary the quantity of other factors, for example, change the quantity (or usage) of capital, e.g. to install a new machine.

The speed with which different kinds of factors can be varied largely depends on the time period under consideration. Here we assume that the firm is making decisions within two time periods — the short-run and the long-run.

The Short-Run and the Long-Run:

The distinction between the short-run and the long-run is based on the difference between fixed and variable factors. A factor of production is treated as a fixed factor if it cannot easily be varied over the time period under consideration. On the other hand, a variable factor is one which can be varied over the time period under consideration.

The Short-Run:

The short-run refers to the period of time over which one (or more) factor(s) of production is (are) fixed.

In the real world, land and capital (such as plant and equipment) are usually treated as fixed factors. Here we are considering a simple production process with only two factors. We treat capital as the fixed factor and labour as the variable factor.

Thus, output becomes a function of (i.e., output depends on the usage of) the variable factor labour working on a fixed quantity of capital. In other words, if the firm wishes to vary its production in the short-run, it can do so only by changing the quantity of labour. With a fixed quantity of capital, this necessitates changing the proportions in which labour and capital are combined in the production process.

The Long-Run:

On the other hand the long- run is defined as the period over which all factors of production can be varied, within the confines of existing technology. In the long-run all factors are variable. Moreover the long-run also permits factor substitution. More capital and less labour or more labour and less capital can be used to produce a fixed amount of output.

In the language of R. G. Lipsey and C. Harbury:

“The long-run is the period that is relevant when a firm is either planning to go into business or to expand, or contract, its entire scale of operation. The firm can then choose those quantities of all factors of production that seem most suitable. In particular, it can opt for a new factory of any technologically feasible size. However, once the planning decision has been carried out— the plant built, machines purchased and installed, and so on—the firm acquires fixed factors and it is operating in the short run.”

The Boundary Between the Two:

The boundary between the short-run and the long- run is not defined by reference to any calendar—a year, or a month or a quarter. It varies from industry to industry and from time to time within the same industry. In most plantation industries the long-run is 15-20 years. For example, rubber trees require a very long time to grow. On the other hand, in a barber’s shop it may be just a week.

A barber may require only a few days to make all types of changes in his small shop. In fact, the boundary between the two runs is defined only in terms of the fixity of one factor of production. The length of the short-run is influenced by two sets of considerations technological (such as how quickly equip­ment can be manufactured or installed) and economic (such as the price the firm is willing to pay for equipment).

We may now turn to a consideration of how output varies in response to input changes in the short run as also in the long run. It may be noted, at the outset, that short-run output changes reflect changes in the proportions in which factors are combined.

On the other hand, long-run changes in output reflect changes in the entire scale of operation. In other words, in short-run we study the returns to a variable factor (such as labour) and in the long-run we study the return to scale. It is, of course, possible to study the nature of return to a variable factor in the long-run, as we shall see later in this article.

Returns to a Variable Factor in the Short-Run:

In the short-run we study the behaviour of output as more and more units of a variable factor (labour) are applied to a given quantity of a fixed factor. So output becomes a factor (capital) function of labour input alone. If this is so the short-run production function may be expressed as: Q = f (L), where the symbols have their usual meanings.

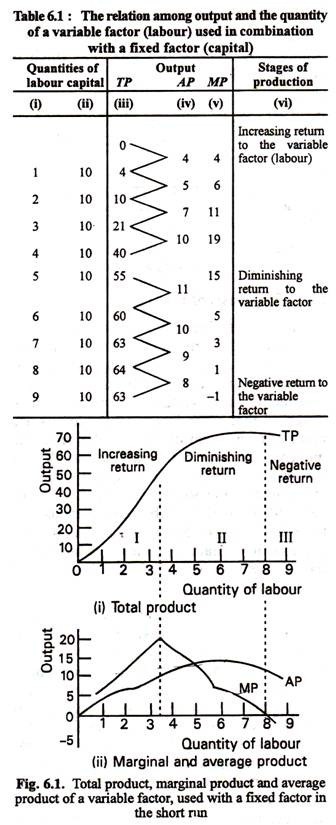
Table 6.1 illustrates the relationship between input changes and output changes in the short run. Three concepts bear relevance in this context, viz., total product (TP), average product (AP) and marginal product (MP). Here Q is total product. It refers to the total amount produced by all the factors employed in a fixed time period. AP is output per unit of input. It is calculated by dividing TP by the amount of the variable factor, e.g., labour (L).

So AP = TP/L = Q/L. is output per unit of labour or per worker. The marginal product is defined as the change in total product associated with a small change in the usage of the variable factor. It may be expressed as

MP = ΔQ/ΔL where ‘A’ denotes any change.

Thus, MP is the ratio of the change in Q and change in L.

The data presented in Table 6.1 are shown graphically in Fig. 6.1. In Table 6.1 we show the total product that results from employing 1 to 9 units of labour [Column (i)] in combination with a fixed quantity (10 units), of capital, [column (ii)]. Column (iv) shows the corresponding AP figures. Each figure of column (iv) is arrived at by dividing each element of Column (iii) by the corresponding element of Column (i). Column (v) gives the MP figures.

Each element in this column shows the contribution (addition) made to the total product (TP) by the one additional unit of labour. In other words, MP is the change in total product which results from a change in the usage of the variable factor (i.e., labour) by one unit. For example, when one unit of labour is employed, TP is 4. When two units are employed, TP is 10. Therefore, the anti­cipation of the said unit of labour is 10 – 4 = 6 units. This is the MP of labour.

The Law of Variable Proportions:

If we look at Table 6.1 carefully we can identify three stages of the production process in the short-run:

(1) In the first stage, when additional units of labour are employed, TP increases more than proportionately and MP also increases. This is the stage of increasing return to the variable factor (labour).

(2) In the second stage TP increases no doubt, but not proportionately. In other words, the rate of increase of TP falls. This means that MP diminishes. This is the stage of diminishing return to the variable factor (labour). This is perhaps the most important stage of the production process in the short run.

(3) In the third stage, TP itself diminishes and the MP is negative. This is the stage of negative return to the variable factor (labour).

The three stages together constitute the Law of Variable Proportions. Since the second stage is most important from the practical point of view, we often ignore the other two stages in most discussions. This is why the Law of Variable Proportions is also known as the Law of Diminishing Returns, which is universally applicable.

The Law states that “when increasing quantities of a variable factor are used in combination with a fixed factor, the marginal and average product of the variable factor will eventually decrease.” In our example AP increases until 5 men are employed. It declines thereafter. MP declines earlier. It rises until 4 men are employed and declines when 5 and more men are employed.

No doubt, the data presented in Table 6.1 are hypothetical. But the relationship shown among TP, MP and AP is widely applicable. From Table 6.1 we may also discover the relationship between MP and AP.

Three points may be noted in this context:

1. So long as MP exceeds AP, the AP must be rising.

2. Thus, it follows as a corollary of this that only when MP falls below the level of AP, does AP fall.

3. Since MP rises when MP is exceeding AP, while AP falls where MP is less than AP, it follows that where AP is at a maximum, it is equal to MP. This is why; the MP curve intersects the AP curve at the latter’s maximum point. (The relation between the margin and the average is mathematical.)

In this context we may note that MP can be zero or negative, but AP can never be so. AP may be very small but is always positive as long as TP is positive. However, such a situation does not carry any significance. In an example where 9 men are employed, TP falls. So no profit-maximising producer would consider employing so many workers.

There are two interpretations of the law of diminishing returns. See Fig. 6.2 which is self-explanatory.

The Basis of the ‘Law’:

Why does the law hold? The answer to this question is that the application of varying quantities of one factor to a fixed quantity of another changes the proportions in which the two factors are combined. In practice, it is observed that some factor combinations are more efficient than others.

As the producer moves towards the best combination, MP and AP tend to rise. As, in subsequent stages of the production process, he moves beyond it, MP and AP both fall (because diminishing returns set in). The basic point is that the best combination of factors is the one which gives the optimum scope for division of labour and specialisation.

In the short run it is not possible to install a new machine or increase the size of an agricultural farm. So, more men are usually employed in conjunction with a fixed amount of capital or land. Thus, if in the short run it is not possible to increase the usage of all factors, there will be a change in the factor proportion.

Suppose 10 workers can cultivate a plot of land in the best possible way. If more men are employed the opportunities for specialisation will gradually diminish (because each may get into other’s way) and diminishing returns set in.

The Law of Diminishing Returns is also known as the Law of Non- proportional Returns. The Law may be stated as : If, in the short run, it is not possible to change the usage of all factors or change them strictly in proportion, output will follow the Law of Non-proportion Returns (because every extra unit of variable factor will gradually make less and less contribution to the total product).

The proximate reason for diminishing returns is the presence of a fixed factor which is used with variable factors. Thus, the Law operates in agriculture due to fixity of land as a factor. If too many workers are employed on land, TP will fall. It is because there were too many workers that got into each other’s way. So the law would not operate if the farmer brought more land under the plough, along-with more hired workers.

In this case, however, we would no longer be considering the application of varying quantities of one factor together with a fixed factor (land). Thus if both the factors — land and labour — were varied the law would not operate. Thus, in short, the law of diminishing returns refers only to the effect of varying factor proportions.

Consequence of the ‘Law’:

If the law did not operate, i.e., if MP were constant, it would simply be possible to increase food production of a country by employing more and more workers on a fixed plot of land. In that case there would be no food problem due to population growth.

It would be possible to feed the entire world by employing more and more workers on the fixed amount of land in the world! However, this does not happen in reality. Instead, a rise in the proportion of labour to land would be found, eventually, to lead to diminishing returns — a continuous decline in marginal product as more and more-workers are employed on a fixed plot of land.

The land area of the earth is fixed. So the only way to avert the operation of the law of diminishing return is to introduce techno­logical progress in agriculture. An example of this is Green Revolution which has succeeded in most developing countries of Asia and Africa.

There is no denying the fact that in the absence of rapid technological progress in agriculture, population growth will ultimately lead to a steady decline in the living standards of the people in most parts of the world.

Where Does the Law Apply?

The Law of Diminishing Returns is operative not only in agriculture but also in various other fields of production.

(i) Buildings:

In the case of buildings, it has been found that the costs of construction increase more in proportion to the height of a building after a certain level. Hence, it is not always profitable to build tall houses. This is an example of the operation of diminishing returns.

(ii) Mines:

The law is applicable to mines also. In a coal mine, as the mine goes deeper the cost of raising coal increases propor­tionately because costlier machinery and equipment have to be used.

(iii) Fisheries:

The law is operative in fisheries also. With the application of additional amounts of labour and capital, the additional catch of fish does not increase in proportion.

(iv) Manufacturing:

The law operates in manufacturing industries under certain circums­tances. A factory with a definite quantity of machinery is capable of producing a certain quantity of goods. If we try to produce more than this amount by using more labour and raw materials, while keeping the machinery unchanged, the cost of production per unit will go up. This means that increase of labour and raw materials beyond a certain point yields proportionately less.

This is an example of diminishing returns. If the factory increases its machinery and other equipment, along with labour and raw materials, this situation will not arise and returns may increase more in proportion, Equipment and machinery can only be increased in the long run. Hence, we can say that the law of diminishing returns operates in industries in the short run, i.e., so long as the machinery and equipment are unchanged.

Prof. Alfred Marshall believed that the law of diminishing returns was particularly operative in those fields of production where the various gifts of nature play a predominant part, e.g., agriculture, mining, fisheries, etc. He also thought that in the case of industrial production, where human labour and capital are important, the laws of diminishing and increasing returns could be operative depen­ding upon circumstances and under different conditions.

As he put it, while the part which nature plays in production shows a tendency to diminishing returns, the part which man plays shows a tendency to increasing returns. According to this view, the laws of dimini­shing returns and increasing returns are particular aspects of a more general principle regarding the employment of factors of production. This general principle is known as the Law of Variable Proportions.

Importance of the Law:

The law of variable proportions carries economic significance. In fact, cost of production and productivity of factors are closely interrelated. More specifically, cost and productivity are the reciprocal of each other. If MP increases, a business firm’s marginal cost of production will fall. Similarly, if AP increases, average variable cost will fall. The converse is also true.

This is why the Law of Diminishing Return is also known as the Law of Increasing Marginal Cost. In fact, a firm’s short-run marginal and average cost curves are U-shaped due to the operation of the Law of Diminishing Returns.

Returns to Scale:

Returns to Variable Factors in the Long Run:

In the short run, the only way to change the volume of output is to alter the usage of the variable factor. A change in the quantities of the variable factor leads to a change in the factor proportions. The long run, however, refers to a period of time over which all the factors of production can be varied. When this is done, holding factor proportions cons­tant, the production function-is said to exhibit returns to scale. For instance, a profit- maximising firm might double the usage of both labour and capital.

When there is a change in the scale of operation of a business firm the law of diminishing returns does not operate. Since all factors are variable in the long run we may find that returns to scale increase decrease or remain constant.

The law of diminishing returns deals with short-run situations in which some factors of production are fixed in supply. However, in the long run, it is possible to vary the use of all factors of production employed. More land can be acquired, more machines installed and more buildings constructed.

This means that in the long run it is possible to change the scale of activities (operation) of a firm. The truth is that a change in the scale takes place when the quantities of all the factors are changed by the same proportion so that there is no change in the proportions in which they are combined.

It is to be noted that when the scale of production is changed, output changes are not proportionate. When a firm doubles its size, output may rise by more than 100%, exactly 100% or less than 100%. The relationship between changes in scale and changes in output are described as returns to scale.

It is widely believed that in a typical production activity, when scale of operations is first increased, increasing returns to scale are observed; ultimately, with the exhaustion of all economies, there is constant return to scale; if expansion is carried far enough, returns to scale decrease.

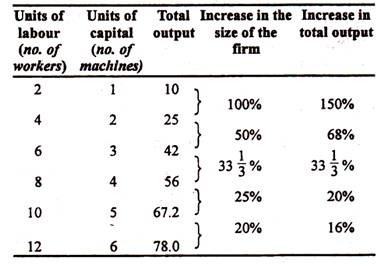
Table 6.2 shows increases in total output as the scale of production increases:

Table 6.2: Returns to Scale

Table 6.2 shows that initially there is increasing return to scale, then constant return to scale and finally decreasing return to scale. A related point may also be noted in this context. There may be diminishing returns to a factor and increasing returns to scale at the same time.

Table 6.2 shows that the firm increases its size but the proportion between the factors remains unchanged (i.e., 1 unit of capital per 2 units of labour). As the size of the firm increases from 2 workers and 1 machine to 6 workers and 3 machines, it experiences increasing returns to scale (output increase more than proportionately).

A change in scale from 6 people and 3 machines to 8 people and 4 machines yields constant returns to scale (size and output change by the same percen­tage). Any further growth in the size of the firm yields decreasing returns to scale because output increases less than proportionately.

Increasing Returns to Scale:

A situation of increasing returns to scale can be attributed to two considerations indivisibilities of some factors and advantages of specialisation.

1. Indivisibilities:

The inability to divide certain factor units into smaller units without either complete loss of usefulness in production or partial loss in efficiency results in a relatively low output per unit of input when operations are conducted on a very small scale.

In other words, in some instances it is not possible to adjust all factors in the same proportion upward or downward. Certain types of capital goods, for example, will not perform their function if they are built on too small a scale, since weight is important in their operation. This is true of various types of capital equipment used in road construction.

Similar patterns are found in warehouse construction; doubling the building material will more than double the amount of usable space. With a rectangular building costs of walls will need to increase only 50 per cent for the capacity of the area to double.

Indivisibilities are not confined to capital goods. Labour also is not completely divisible. One operator may be required for each machine, regardless of its size. A freight train requires one engineer, regardless of the tonnage of the train; there is no way of using a fraction of an engineer on a train of light tonnage.

Within limits, in small enterprises, employees may be used to perform several different tasks. But as a practical matter, there are severe limitations to such possibilities. A switchboard operator may serve as receptionist and do some stenographic work, but she can scarcely be used at the same time as an elevator operator and window cleaner.

A clerk in a store may be busy only 2-3 hours a day. Yet he must be paid for the entire day. In any type of business, it is difficult to utilise each worker to the maximum of his producti­vity at all times. As an establishment grows, the percentage of labour time not utilised should fall, if management policies are effective.

Indivisibilities are also encountered in advertising, research work, and financing. Advertising on a small scale is relatively less effective than on a much larger scale. Industrial research activities cannot be carried on effectively on a small scale. Indivisibilities are also found in the financing of a business. The cost of floating a bond issue, for example, is to a large extent independent of the size of the issue.

Thus, this method of financing — the cheapest method when large, amounts of capital are to be obtained — is expensive to a firm until it has expanded beyond a certain size. The refusal of many investors to consider the bonds of any except well-known companies increases the difficulty of bond financing by small firms.

2. Specialisation:

The other and closely related cause of increasing returns to scale is the advantage offered by specialisation. In a very small business, employees must perform a wide variety of tasks. As the size of enterprise increases, each employee can be used in a relatively specialised job, with a consequent increase in output per worker. The advantages of specialisation of labour have been recognised since the days of Adam Smith.

The primary advantages include the greater skill acquired with specialisation, the avoidance of wasted time in shifting from one task to another, and the employment of persons best suited to particular types of work. In managerial activity as well as in other phases of work, advantages of specialisation are encountered.

As a firm grows in size, personnel relations will be conducted by a specialist; traffic management will be in the hands of a full-time traffic expert instead of being performed by a person who also has various other tasks. Specialisation is also possible with capital equipment.

As a firm increases its scale of operations, it becomes possible to replace non-specialised equip­ment which is capable of performing a number of tasks by specialised equipment designed for various specific operations, with a consequent increase in output per unit of input.

The importance of the phase of increasing returns depends in large measure upon the type of production process involved, hi almost any type, increasing returns are likely to be encountered to some extent when a business expands from a very small initial size because of indivisibilities of labour. If, however, a firm utilises very little capital equipment, and if few advantages of specialisation of labour are derived, increasing returns may very quickly come to an end.

On the other hand, if a firm uses extensive amounts of capital goods of types which cannot be used efficiently on a small scale, there may be very substantial increasing returns (extending over a large volume of output). Thus, increasing returns are very important in steel, cement, and automobile industries, while they are of much less importance in agriculture and retailing.

Constant Returns to Scale:

As a firm continues to expand its scale of operations, it gradually exhausts the econo­mies responsible for increasing returns. A firm will eventually grow to the point at which it is using the best type of capital equipment available and is enjoying full advantages of specialisation of labour. Beyond this point, further increases in the scale of operations are likely to produce more or less constant returns for a substantial range of output. If the entire scale of operations is double, output will approximately also double.

However, constant returns to scale are relevant only for time periods in which adjustment of all factors is possible. If a firm doubles output in a short period with a fixed physical plant which was previously utilised to normal optimum capacity, returns per unit of the variable factors will decline because of the operation of the Law of Diminishing Returns. But if factors are varied, as may be possible over a long period of time, the law of diminishing returns will not operate.

Decreasing Returns to Scale:

As a firm continues to expand its scale of operations, beyond a certain point there is apparently a tendency for returns to scale to decrease, and thus a given percentage increase in the quantities of all factors will bring about a less than proportional increase in output. It is believed, however, on the basis of actual studies, that a long phase of constant returns is usually observed.

Decreasing returns to scale for the firm itself are usually attributed to increased problems and complexities of large-scale management. Continued increases in entre­preneurial activity beyond a certain point encounter more and more serious problems and difficulties. An increasing percentage of the total labour force will be required in administrative work, in order to provide coordination of the activities of the enterprise and necessary control over the large numbers of employees.

A growing concern, once it reaches substantial size, encounters a funda­mental problem of management; final authority for basic policy must remain in the hands of a group of men who control the operation of the business. Yet these men are far removed from the actual level of operations. They are forced to make decisions on the basis of second ­hand information, on subjects with which they have no direct contact. Furthermore, subs­tantial delay can occur in the making of decisions as the size of the firm increases.

The causes of falling efficiency as the size of the firm increases are described as diseco­nomies of scale. One possible cause of such diseconomies seems to be the limited supply of entrepreneurs. As G.F. Stanlake has put it, “while the inputs of land, labour, and capital may be increased proportionately, this may not be possible with regard to management ability. The entrepreneurial skills required to manage large enterprises are, it seems, limited in supply so that it is often difficult to match the increase in the supply of other factors with a corresponding increase in the supply of management ability.”

The growth of a business also increases the amount of division of responsibility and serves to lessen initiative, especially on the part of persons in lower-level jobs who are in a position to bring desirable changes. With increased size comes loss of personal contact between management and workers, with consequent loss of moral and increase in labour troubles.

Distinction between Return Factor and Return to Scale:

The law of diminishing marginal physical productivity applies only to the short-run. It describes the additional output that is produced when additional units of a variable input are combined with a particular quantity of a fixed input.

Economies and diseconomies of scale and increasing, constant, and decreasing cost industries are concepts that apply to the long run. Economies and diseconomies of scale refer to an individual firm. Increasing, decreasing, and constant costs refer to an entire industry.

Economies and diseconomies of scale describe what happens to a firm’s costs as the firm increases production and no other firms influence it. The shape of the firm’s long-run average cost curve is determined by the extent to which the firm experiences econo­mies and diseconomies of scale.

The production function shows increasing returns to scale if an equal percentage increases in all inputs results in a more than proportionate increase in output. Suppose a firm uses only two variable factors, say, labour and capital. Assume that the firm doubles its use of both labour and capital.

If, as a result of this, output gets more than doubled, there are increasing returns to scale. If, when inputs are doubled, output is exactly doubled, return to scale are constant. If, finally, doubling of capital and labour causes a less than proportionate increase in output, then decreasing returns to scale are said to be operating.

These three cases are illustrated in Fig. 6.3. In all the three sections of the diagram we show the short run average and marginal product as variable amounts of labour are employed in two plants.

In the short run, the firm of different sizes is restricted to one of the two plants or is supposed to have a fixed plant. This means that its production capacity is fixed. So output changes are associated only with changes in the usage of the variable factor, labour. This is why in the short run we study the return to a factor and in the long run we study the return to scale.

Since in the long run the firm can choose to operate either plant, long-run changes consist of moving from one set of short-run curves to another. This is done by altering the usage of capital. The short-run curves are labelled SAP₁ and SMP₁ for the smaller plant; and SAP₂ and SMP₂ for the larger plant, which is assumed to use exactly double the quantities of capital as the smaller plant.

Constant Return to Scale:

In Fig. 6.3(i) it is clear that the production process exhibits constant returns to scale. Suppose the firm is operating at point c or SAP₁, at which average product is at a maximum, i.e., the quantity of labour is L₁ and output per worker, on an average, is L₁c.

The firm then builds a new plant of double the size of the original plant. Moreover, the quantity of labour employed is also doubled. As a result output also gets doubled, or, output per unit of factor input remains unchanged. Here in Fig. 6.3(i) L₁c = L₂d. Since output changes in exact proportion to inputs, returns to scale are said to be constant.

Increasing Returns to Scale:

Fig. 6.3(ii) shows that when inputs are doubled output is more than doubled. This means that average product of input increases. Suppose, as in the previous case, that the firm moves from the smaller plant to the larger plant, thereby doubling its amount of capital. It also uses double the quantity of labour OL₂ is exactly twice the quantity of labour OL₁.

Now average product rises L₂h is greater than L₁g. If average product per unit of labour rises when labour and capital inputs are doubled, then total product is more than doubled. This means that the production function is showing increasing returns to scale.

Decreasing Returns to Scale:

In Fig. 6.2(iii) we illustrate a situation when there is decreasing returns to scale. In this case, we observe that doubling of the size of the plant and of labour inputs lowers average product from L₂n to L₂m. Consequently output is less than doubled.

Diminishing Return to a Variable Factor and Increasing Returns to Scale:

Fig. 6.3 shows that a firm’s production process may show both diminishing return to a variable factor and increasing returns to scale. There is no contradiction or logical inconsistency between the two relationships. The following table clarifies the point: 

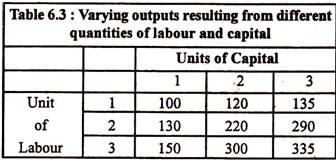
Table 6.3: Varying outputs resulting from different quantities of labour and capital

Table 6.3 shows total output that is associated with different quantities of labour and capital that are being used in the production process. The table enables us to calculate the marginal product of either variable factor (labour and capital). It can also be used to identify the nature of returns to scale.

Suppose we want to calculate marginal product of capital. We have to keep labour constant (say, at one unit). When one unit of capital is used with one unit of labour, output is 100 units. If 2 units of capital are used, keeping the quantities of labour fixed at 1, output increases to 120. So the marginal product of capital is 20. If another unit of capital is used, output increases to 135, or marginal product of capital is 15. Thus, the marginal product of capital is diminishing.

Now let us keep capital constant and increase the usage of labour. If 2 workers are employed, holding capital fixed at 1 unit, total product increases from 100 to 130 and marginal product of labour is 30. In the next stage output increases to 150 when one extra worker is employed. So marginal product of labour is 20. Again the marginal product of labour is diminishing.

Now suppose both the inputs are doubled at the same time. As a result output increased from 100 to 220. This is a case of increasing returns to scale. If, now, 3 units of capital and labour are used (i.e., if there is 50% increase in the quantity of capital and labour) output increases from 220 to 335 (which shows more than 50% increase in output). Thus the production function again exhibits increasing returns to scale. In each case the factor pro­portion remains constant (1: 1 = 2: 2 = 3: 3).

Thus, from this exercise we learn an essential lesson exactly the same figures of the productivity of labour and capital can yield diminishing returns to each variable factor, but increasing returns to scale. The reason is not far to seek; the law of dimini­shing returns relates to varying of one input while holding the other constant, while the relations of returns to scale refer to the varying of both inputs.

Distinction between Economies of Scale and Returns to Scale:

The two concepts, viz., economies of scale and returns to scale create confusions. Econo­mies of scale reduce average cost as the scale of production increases, while returns to scale are concerned with physical input and output relationships.

If, for example, the usage of factors were to increase by 150%, the production process under consideration would be said to be experiencing increasing returns to scale. Conversely, if inputs were to be increased by 100% but output were to increase by less than this, then the production function would exhibit decreasing return to scale.

Increasing returns to scale lead to decreasing cost. However, it is not essential that every economy of scale which reduces cost is a result of return to scale. A simple example may clarify the point. Bulk-purchase of raw material may be a source of internal economy for a firm but it does not involve returns to scale since there is no change in the input/output relationship.

Determinants of Returns to Scale:

There are two major determinants of increasing returns to scale:

(1) indivisibilities and

(2) the principle of increased dimensions.

There are certain other determinants of constant and decreasing returns. We may now make a brief review of these determinants.

1. Indivisibilities:

A large firm can afford to employ large and specialised machinery. Moreover, the firm has large output to fully occupy the machine for a long period of time and, therefore, it can be operated efficiently. Indeed some machines are indivisible in the sense that they are only efficient if they are large in size, for example, blast furnaces. Small firms cannot afford to purchase these large, indivisible machines and do not produce an output large enough to keep that fully occupied over a long period.

2. The Principle of Increased Dimensions:

Large machines sometimes lead to fall in costs per unit of output. This is because a large machine can cater for a much larger output. But this may involve only a slightly greater cost. For example, a double-decker bus can carry twice number of passengers as a single decker at the same total fixed cost. Moreover, only the same labour is required. A large oil tanker can carry twice as much oil as a smaller tanker, but needs only a few more workers to operate it. This is called the economy of increased dimensions.

These two determinants of returns to scale are inter-related. The principle of increased dimensions illustrates the idea that indivisi­bilities lie behind the existence of increasing returns to scale. The volume of output has to be large enough so as to make the best possible use of specialised technique, often capital intensive, especially in the manu­facturing industries where standard products are mass produced in the long run.

Bases of Constant and Decreasing Returns:

The most common explanation of the appearance of constant and decreasing returns to scale lies simply in the exhaustion of the bases for increasing returns. Sometimes the reason may be purely technological —larger machines may be more efficient up to a certain point but not always so. If such machines are intensively used, a stage is often reached in the long run when such machines lose their efficiency and effectiveness.

One of the common explanations of decreasing returns to scale, however, relates to manage­ment. With an increase in the scale of operations of a business firm there are problems of management coordination, so that business efficiency declines when top management loses track of all sections of a business.