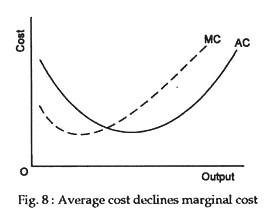
Since marginal and average cost are measured in the same units, and are derived from the total cost curve, the relationship between the two is particularly important.
Starting from a zero level of output, AVC and ATC fall as output increases so long as MC is lower than AVC and ATC. Beyond this point MC rises above AVC and ATC, and AVC and ATC then rise as output is increased. This relationship is reflected in Fig. 8 by the fact that the AVC and ATC curves decline over the range where the MC curve is below them and increase over the range where the MC curve is above them. It, therefore, follows that the MC curve passes through the AVC and ATC curves at their minimum points.
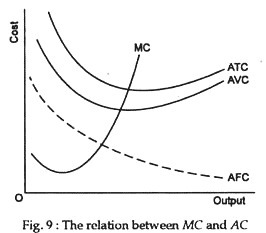
The reason for this relationship between the marginal magnitude Mc and the average magnitudes AVC and ATC -is strictly mathematical and is shown in Fig. 9. Suppose that a basketball team scores 80 points in its first game and 90 in its second. Its average scope per game is, therefore, (80 + 90)/2, or 85 points per game — the total number of points scored in both games divided by the number of games.
Now, if the team scores less than the average in the third game, say 70, the average number of points scored per game will decline from 85 to (80 + 90 + 70)/3, or 80. On the other hand, if the team scored 100 points in the third game, the average number of points scored per game would increase from 85 to (80 + 90 +100) 3 = 90.
The same thing is true of costs. When the addition to total cost (the marginal cost) associated with the production of another unit of output is greater than ATC, ATC rises. Conversely, if the marginal cost of another unit is less than ATC, ATC will fall. Hence, ATC declines as long as MC is above ATC. When MC is above ATC, ATC rises. Therefore, at the output level at which MC rises from below ATC to just above it, ATC ceases to decline and begins to rise.
It follows, therefore, that ATC reaches its lowest point at the output level at which MC crosses ATC. Exactly the same argument applies to AVC. There is no such relationship between MC and AFC, however. This is so because AFC depends upon TFC and since TFC is un-effected by changes in TVC, AFC declines continuously as output changes no matter what the behaviour of MC.
Three points are to be noted in this context:
ADVERTISEMENTS:
(1) When ATC is falling MC < AC;
(2) When ATC is constant MC = AC; and
(3) When ATC is increasing MC > AC.
However, it is not necessarily true that when ATC is falling MC will also fall.