In this article we will discuss about the relationship between price elasticity of demand and marginal utility.
We often draw a distinction between necessities and luxuries. While it is possible to do without a luxury good like a VCR it is not easy to go without a necessary good to one individual may be a luxury good to another individual.
Yet, this distinction makes some sense if we compare the total utility that households derived from consumption of different commodities. Total utility derived from a commodity is measured by the area under the demand curve. So, it is very much on the high side in case of a necessity. But, the total utility of a luxury is very much on the low side.
Yet, we often make the mistake of trying to use our knowledge of total utility to predict price elasticity of demand. We often loosely make the statement that, since we can easily give up the consumption of luxuries, their demand is highly elastic. When their prices rise, consumers can dispense with them. By contrast, the demand for necessities is highly inelastic because, when prices rise, households cannot cut their consumption of these items very much.
ADVERTISEMENTS:
However, the fact is that elasticity of demand depends not on total utility but on marginal utility. In fact, marginal utility indicates the consumers’ willingness to pay for a commodity. Consumers will be ready to buy more and more units so long as marginal utility exceeds the market price of the commodity. Each household will stop purchasing the commodity when marginal utility, i.e., utility derived from the last unit consumed is greater than or at least equal to its price.
A price rise will lead to a fall in the quantity demanded of a commodity. But, by how much will consumption, whose price has gone up, have to fall to increase its marginal utility to the consumers depends on the shape of the demand curve, i.e., its elasticity in the relevant range. And elasticity of demand is determined not by total utility but by marginal utility over the same range.
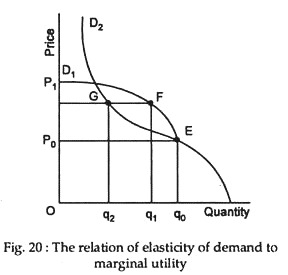
This point is illustrated in Fig. 20. Here, we consider two demand curves D1 and D2 which coincide at point Z. Suppose, the original price is P0. Whether the demand curve is D1 and D2, the household consumes Q0, where the marginal utility is equal to price. Suppose price rises to P1. Consumption will obviously fall. But, by how much? It all depends on price elasticity of demand.
The two demand curves show quite different responses to price change. If the demand curve is fairly elastic over the range of price change (P0P1), i.e., consumption has to fall from Q0 to Q2 as can be found out by comparing points G and E. If, on the other hand, the demand curve is fairly inelastic in the relevant range, i.e., D2, a small decrease in consumption (from Q0 to Q2) is enough to raise marginal utility sufficiently and make it equal to the new price P1.
ADVERTISEMENTS:
Thus two points are to be noted here:
1. The first point is that, market behaviour is not affected by total utility but by marginal utility. So, total utility of one demand curve may be higher than that of another. But, it has no relevance in measuring price elasticity of demand.
2. The second point is that, the shape of the demand curve over the range of price change (P0 P3) is irrelevant for determining price elasticity. This means that only the arc EP of D1 and are EG of D2 are relevant here.
ADVERTISEMENTS:
Conclusion:
Despite the limitations found in this law, it has a great deal of practical importance. As most of the people are assumed to be rational, they behave, consciously or un-consciously, in accordance with this principle for maximising the gains and minimising the losses. For this reason, Chapman remarks, “we are not, of course, compelled to distribute our incomes according to the law of substitution or equi-marginal expenditure.”