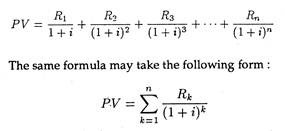Concepts of Managerial Economics (With Diagram)

The following points highlight the seven fundamental concepts of managerial economics. The concepts are: 1. The Incremental Concept 2. The Concept of Time Perspective 3. The Concept of Discounting Principle 4. The Opportunity Cost Concept 5. The Concept of Equimarginal Principle 6. The Contribution Concept 7. The Concept of Negotiation Principle.

Managerial Economics: Concept # 1.

The Incremental Concept:

It is easy to describe incremental reasoning. But it is very difficult to apply it. As T.J. Coyne has put it, “It involves estimating the impact of decision alternatives on costs and revenues, stressing the changes in total cost and total revenue that result from changes in prices, products, procedures, invest­ments or whatever may be at stake in the decision”.

Two basic concepts lie at the heart of incremental analysis, viz., incremental cost and incremental revenue. The former refers to the change in total cost resulting from a decision. Likewise, the latter may be defined as the change in total revenue re­sulting from a decision.

A decision is surely profita­ble if:

1. It increases revenues more than it increases cost.

2. It reduces some cost more than it increases oth­ers.

3. It increases some revenues more than it de­creases others.

4. It decreases costs more than it decreases reve­nue.

We may now consider some of the implications of incremental reasoning which appears to be too elementary. In general, businessmen think that in order to make an overall profit they must make a profit on every activity (or job).

Consequently they refuse orders that do not cover cost (labour, materi­als and overhead) and make a provision for profit. This is an unproved and probably a false belief. In­cremental reasoning makes it clear that this rule may be inconsistent with short-rim profit maximi­zation.

A refusal to accept a job below cost may im­ply rejection of a possibility of adding more to reve­nue than to cost. Here the relevant cost for decision-making is not the full cost but rather the incremen­tal cost. The following example clarifies the point. Consider a new order which is supposed to bring Rs. 9,000 additional revenue.

The costs are estimat­ed as follows:

It apparently seems that the order is unprofita­ble. But suppose there is idle capacity in the short run. This could be used to produce the order. Sup­pose acceptance of the order will add only Rs. 900 of overhead.

Suppose neither extra selling cost nor extra administration cost is involved in the order. Moreover, only part of the labour cost is incre­mental, since permanent workers; who are sitting idle, may be put to work without extra pay.

Suppose the incremental cost of accepting the order is as follows:

Although at first sight it appeared that the or­der would results in a loss of Rs. 1200, it is now clear that it will bring an additional profit of Rs. 2,800.

However, incremental reasoning does not mean that the firm should fix the price at incremental cost or should accept all orders that just cover incre­mental costs. True, ‘charging what the market will bear’ is quite consistent with instrumentalism, for it implies raising prices as long as the resulting reve­nues increase.

In our example, the acceptance of the Rs. 9,000 order is based on assumption that there is idle capacity which could be fruitfully utilized to execute the order. It is also implicitly assumed that there is no other profitable alternative. If there is a more profitable alternative, it has to be accepted.

So the essence of the incremental principle is that: a decision is to be considered as sound and ra­tional if it increases revenue more than it increases cost, or reduces cost more than it reduces revenue.

Marginalism:

Incremental reasoning is closely related to two important concepts of traditional ec­onomics, viz., cost and marginal revenue. However, there are similarities and differences.

The follow­ing two points may be noted in this context:

1. Marginal cost and revenue are always defined in terms of unit changes in output, but incremental cost and revenue are not necessarily restricted to unit changes. Usually marginal cost is expressed as the ratio of two absolute changes, viz., change in total cost and change in output, i.e., MC = dC/dQ. Likewise MR = dTR/dQ where MR is marginal rev­enue and TR is total revenue.

A simple example will illustrate the two con­cepts: the marginal concept and the incremental concept. Suppose, the extra cost of producing one ex­tra unit of output is Rs. 10 and the extra revenue made by selling this extra unit is Rs. 15.

If a 5-unit increase in output increases total cost by say Rs. 45 (from say Rs. 350 to Rs. 395), and increases revenue by Rs. 70 (from say Rs. 400 to 470), we can speak of an incremental cost of Rs. 45 and an incremental revenue of Rs. 70. In this case the unit (average) MC over this range of output is Rs. 9 and unit (average) MR is Rs. 14.

2. Incremental concepts are more flexible than marginal concepts. In general we restrict the two terms: MC and MR to the effects of changes in out­put. But managerial decision making is not to be concerned with changed output at all. For example, the production manager may be faced with the problem of substituting one process of production (or activity) for another to produce the same output.

The problem here is one of comparing the cost of the first process with -that of the alternative. Marginal analysis is not suited for this type of de­cision. It is, of course, possible to compare the MC of one process with that of another but not of the MC of the change.

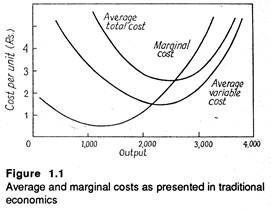
However, the term ‘incremental cost’ may be used to refer to the change in cost brought about by the changes in production process or activity.The following diagram may be used to compare the marginal and incremental approaches. In Fig 1.1 the MC curve is rising over most of its range.

Suppose the production manager is considering an increase in output from 2,000 to 3,000 units. In this case it is very difficult to measure the marginal cost of change. No single MC cost figure will suffice. The MC is initially low, but subsequently it rises rapidly.

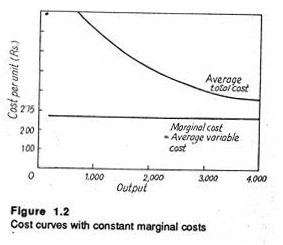
However, another pattern of costs is common in industry. Several empirical studies have discov­ered relatively constant marginal costs over wide range of outputs, as in Fig 1.2. Here MC does not change dramatically with the changes in output. Hence a single MC cost figure can be used over the whole range.

For the firm illustrated in Fig 1.2, we assume that total fixed cost is Rs. 4,000 per unit of time. The aver­age variable cost is Rs. 2.50 per unit. The MC is also Rs. 2.50 per unit. Suppose, the production manager has to choose between an output of 2,000 units and one of 3,000 units. In this case MC is Rs. 250 but incremen­tal cost is Rs. 2,500.

The pertinent question here is whether or not marginal costs are in fact constant and justify the substitution of incremental cost measurements over large changes in output, for measurements of cost changes for small (marginal) changes in output. If the short run cost curves were linear throughout, the decision-making problem would be greatly simpli­fied.

Managerial Economics: Concept # 2.

The Concept of Time Perspective:

In economics, we often draw a distinction be­tween the short-run and the long-run. This distinc­tion is not based on any calendar period, say, a month, a quarter or a year. It is based in the speed with which decisions can be made and factors of production varied.

The period during which it is possible to vary some factors and not others is called the short run. But the period during which all factors can be varied is called the long-run. For example, more output can be produced in the short- run by using more labour and raw materials. This is basically a short-term decision. But setting up a new factory or building an entirely new plant is a long-term decision.

In reality, however, the distinction between the two often gets blurred. What remains is an estimate of those costs that vary and those that do not by the decision under consideration. In managerial economics we are concerned with the short-run and long-run effects of decisions on revenues as well as on costs.

The line between the short-run and long-run revenue (or demand) is even less transparent than that for costs. What is really important for managerial decision making is main­taining the right balance among various runs, i.e., the long-run, short-run and intermediate-run per­spectives.

A decision may be made on the basis of certain short-term considerations but it may have various long-term repercussions which, in turn, may make it more or less profitable than it appeared at the first sight. A simple example will make this point clear.

Suppose there is a firm with temporary idle ca­pacity. It now gets an order for 10,000 units. The prospective customer is willing to pay Rs. 3 per unit, or Rs. 30,000 for the whole lot. The short-term incremental cost (which ignores the fixed cost is) is only Rs. 2.50. So the contribution to overhead and profit is 50 paise per unit (or Rs. 5,000 in all).

But the following two long-term repercussions must be taken into account:

1. If the management commits itself to a series of repeat orders at the same price, the fixed costs (which are ignored temporarily) will become vari­able cost. For instance, sooner or later it will be­come necessary to replace the machinery and equipment which wear out. True enough, the grad­ual accumulation of orders may require an addition to capacity, with added depreciation and added top-level supervision.

2. If lower price is charged for the extra order, old customers who pay higher price for the same product may become annoyed. This practice will appear to be unethical and may destroy the compa­ny image. This will be damaging in the long-run.

Now on the basis of our above discussion we can state the above principle — the principle of time perspective — in the following words:

A decision should always take into considera­tion both the short-term and long-term effects on revenues and costs, giving proper weight to the most relevant time periods.

However, the real problem is how to apply this principle in specific situations to arrive at a deci­sion.

An example:

A large reputed printing company in Calcutta maintains a policy of never quoting be­low full cost even if it has some idle capacity. Al­though incremental cost is far below full cost, man­agement has found that the long-run repercussions of going below full cost more than offset any short- run gain.

Prima facie, price reduction for some cus­tomers would have an undesirable effect on cus­tomer goodwill, especially among regular custom­ers who will not benefit from rate reductions. Secondly, if the availability of idle capacity is unpredictable, there may be pressure on capacity when demand is high.

In fact when the order be­comes firm the situation might change, causing low-price orders to interfere with regular price business. Management would like to avoid this sit­uation.

Otherwise, it would be considered as a firm that exploits the market when demand is unfavorable and allows price concessions when de­mand is favourable. This simple illustration re­veals the need to consider both the long-term and short-term impact of price policy.

Managerial Economics: Concept # 3.

The Concept of Discounting Principle:

There is a famous proverb that a bird in the hand is worth two in the bush’. This proverb, like many others, contains an element of truth. And one of the fundamental propositions of economic theory is that a rupee to be received tomorrow is worth less than the same rupee received today.

The above proverb is, however, slightly misleading in this context, implying that the reason for discounting the future rupees is uncertainty about receiving them. Even in the absence of uncertainty, it is neces­sary to discount future rupees to make them equiv­alent to present day rupees.

A simple example will make clear the ratio­nale of discounting. If an individual is offered to choose between a gift of Rs. 1,000 today or Rs. 1,000 to be received after one year, he would surely pre­fer the former (even if there is no uncertainty re­garding the receipt of either gift).

This is because in a world where the rate of interest is not zero there is scope for investing Rs. 1,000 at the market rate of interest and accumulate interest on the prin­cipal. If the rate of interest is 5%, today’s Rs. 1,000 will become Rs. 1,050 after one year.

There is another way of illustrating the dis­counting principle. One may ask how much money today would be equivalent to Rs. 100 a year from now.

If the rate of interest is 5% the present value of Rs. 100 to be received after one year is:

Where PV = present value and

i = rate of interest

As a cross check one may multiply the PV of Rs. 95.24 by 1.05 to determine how much money will have accumulated during the year at 5%. The an­swer is Rs. 95.24 x 1.05 = Rs.100. In other words, Rs. 95.24 plus the interest on it will accumulate to an amount exactly equal to Rs. 100.

An individual who can earn 5% on his (or her) money should be in­different between receiving Rs. 95.24 today and Rs. 100 after one year. So the present value of Rs. 100 is Rs. 95.24.

The same analysis can be extended to any num­ber of periods.

A sum of Rs. 100 two years from now is worth:

So a general pattern seems to be emerging.

In general, the present value of a sum to be received at any future date can be found out by using the fol­lowing formula:

in which PV = Present value

r = amount to be received in future

i = rate of interest

n = number of years lapsing between the receipt of R

If the receipts are made available over a num­ber of years, the formula becomes:

where k can take any value from 1 through n.

These formulas are usually to be made use of in any discussion of investment decision and capital budgeting.

The essence of the principle the dis­counting principle may now be summed up in the following words: If a decision affects both costs and revenues at future dates, it is absolutely essen­tial to discount those cost and revenue so as to make them comparable to some present value before a valid comparison of alternatives is possible.

We often find the application of the princi­ple in the business world. Suppose one borrows Rs. 10,000 from a bank on a note. If the note is for Rs. 10,000, the borrower will not get the full value but rather the amount discounted at the appropri­ate rate of interest.

If the discounting rate is 6% and if the note is for one year, the borrower will receive approximately Rs. 9,420. In this case we can say that the present value to the bank of the borrow­er’s promise to pay Rs. 1,000 in a year is only Rs. 942 at the time of the loan.

The principle operates in the bond market as well. The market price of a bond reflects not only its face value at maturity and interest payments, but also the current discount rate. As the market discount rates vary, bond price, vary inversely. Suppose you receive a bond which promises to pay you Rs. 10 per annum, in perpetuity.

If the market rate of interest (the discount rate here) is 10% its PV will be Rs. 10/5% = Rs. 200. If the rate of inter­est goes down to IM-f/o its market prices will rise to Rs. 10/5% = Rs. 400. So it is possible to make a capi­tal gain of Rs. 200 by selling the bond.

The same principle can be applied in case of an individual firm. Suppose a firm is considering buy­ing a new machine. It should estimate the discount­ed value of the added (net) earnings from that ma­chine before venturing out.

The same principles applies if the firm is considering the acquisition (purchase) of another firm or a merger. Likewise, a firm that produces output maturing at varying ages cannot compare the profitability of changing the product mix without invoking the discounting prin­ciple.

Managerial Economics: Concept # 4.

The Opportunity Cost Concept:

The opportunity cost of a decision means sacri­ficing alternatives. Opportunity cost measures the value of the most valuable of the options that we have to forego in choosing from a set of alternative options. Suppose a shipbuilder gets a contract to be called Contract A.

After making the correct assess­ment of the associated incremental costs and reve­nues he arrives at an estimated profit of Rs. 25,000 from the contract. Suppose, in the meantime, two other contracts, B and C, have been brought to his attention.

These two are expected to give a profit of Rs. 15,000 and Rs. 20,000, respectively. However, his yard’s capacity is so limited that he can accept only one of these. So, in the absence of any other consideration, he would accept contract A, the most profitable one.

His opportunity cost would then be Rs. 20,000, the sacrifice he must make of the profit for the next best option. Had he chosen either B or C, his opportunity cost would have been Rs. 25,000 profit that A would have earned.

An opportunity cost has arisen here only because some essential input, the yard’s capacity, is scarce, i.e., grossly insufficient to take up all the options that are open and desirable. In the absence of such a constraint no such sacrifice and hence no opportu­nity cost would have arisen.

We will come across various examples of opportunity cost in this title because all business activity is carried on within constraint (‘scarcities’) which force choices and consequent sacrifices to be made.

The following examples help in understanding the meaning of the term:

1. The opportunity cost (O.C.) of using a ma­chine is the most profitable alternative sacrificed by employing the machine in its present use.

2. The O.C. of buying a colour TV is the interest or profit that could be earned by investing the pur­chase money.

3. The O.C. of working for oneself in one’s own factory is the salary that one could earn in others occupations.

4. The O.C. of funds tied in one’s own business is the interest (or profits adjusted for difference in risk) that could be earned on those funds in other ventures.

However, if machine has been lying idle for some time, the O.C. of bringing it into production is nil. Similarly the O.C. of using idle space is obvi­ously less than that of using space needed for other activities. So O.C.s require the measurement of sacrifices, real or monetary.

If a decision involves no sacrific­es, it is cost free. The expenditure of cash (for raw- materials, say) involves a sacrifice of other possi­ble expenditures and is therefore an O.C. Thus the only costs for decision-making are opportunity costs.

However, all O.C.s do not involve actual mone­tary payments. A man in a desert or in a distant is­land (like Robinson Crusoe) might have the choice between picking coconuts or fishing. The O.C. of co­conuts is the amount of fish that might be obtained with the same amount of time and effort — irre­spective of how much the man likes shinning up trees.

O.C.s are important when considering make-or- buy decisions, as also when deciding whether or not to sell. For instance, the alternative to using busi­ness premises which one owns as offices is to rent or sell them. The O.C.s is the rental forgone, or the difference between the expected market value at the beginning and end of the year, whichever is higher.

One form of opportunity cost which is likely to be used is in the analysis of capital projects. The discount rate used to find out net present values when evaluating capital projects is nothing but an opportunity cost of capital.

The alternative to car­rying out the project is to invest the money in a safe alternative and the evaluation is designed to ascertain whether the project yields a higher re­turn. This concept of O.C. is discussed in the context of capital expenditure decisions later.

Closely related to our above discussion is a dis­tinction between explicit and implicit costs. Explic­it costs are those that are reflected in the book of accounts, such as payments for raw-materials and labour.

On the contrary, implicit (or imputed) costs are those sacrifices (such as the interest on the owner’s own investment) which are not reflected in accounts. Some writers equate O.C.s with implicit costs. The truth is that O.C.s cover all sacrifices, implicit or explicit.

In reality, however, some explicit expenses may not involve sacrifices of alternatives. For example, a company like Texmaco Ltd. paid wages to idle la­bour in periods of slack activity. These wages were in the nature of a fixed cost and were not included in the O.C. in a decision to use that labour in some other activity.

From the above discussion we can derive anoth­er principle — the O.C. principle — as follows:

The cost involved in any decision is the sacrific­es of alternatives required by that decision. In case there is no sacrifice, there is no cost either.

Large firms often make uses of the O.C. concept. They use linear programming models, replacement models and other optimization techniques. These are all based on the O.C. concept.

Managerial Economics: Concept # 5.

The Concept of Equimarginal Principle:

The cornerstone of the economists’ marginal analysis is that purchases, activities, or produc­tive resources should be allocated so as to ensure that the marginal utilities, benefits, or value- added accruing from each, are identical in all uses. Optimality requires that it should not be possible to increase the total benefit or reduce the total cost by moving one unit from one application to another.

If this equimarginal condition is violated, the sys­tem is operating below its optimum and it is possi­ble to gain some improvement by reallocation of in­puts or purchases. The key assumption underlying this result is the law of diminishing returns or var­iable proportions. For the equimarginal principle to operate, the law of diminishing returns is held to apply.

The law implies that the marginal product will decline as more of one resource is combined with fixed amounts of another. This proposition, in fact, holds good over a wide range of economic ac­tivity. For example, successive applications of fertilizer tend to raise cereal yields per acre, but in­creasing quantities of fertilizer are successively re­quired to give equal output increases.

The micro-economic theory of the demand for labour asserts that the profit: maximising entre­preneur will continue to employ labour so long as the resulting addition to his costs is covered by the addition to his receipts from the sale of his prod­ucts.

One of the fundamental principles of economics is the proposition that in input such as labour it should be so allocated among different activities or lines of production that the value added by the last unit is the same in all uses. This generalisation is known as the equimarginal principle.

Consider a simple situation where a firm has 100 units of labour at its disposal. If this remains fixed in the short-run, the total wage bill can be determined in advance. For example, if each work­er gets Rs. 300 per month the total payroll will be Rs. 30,000 per month.

Suppose there are five differ­ent activities in the factory: A, B, C, D and E. Each activity requires labour as an input. With limited supply of labour it is possible to expand any one of these activities by employing more labour only by reducing the level of other activities.

Suppose when one unit of labour is added to ac­tivity A, total output increases by, say, 10 units. By selling this output in the market at a price of Rs. 5 per unit the firm makes a gain of Rs. 50. The value of this added output is called ‘the value of the marginal product (V.M.P.) of labour’ in activity A.

In the same way, we can estimate the value of the marginal product of labour in other activities, viz., B, C, D and E. If V.M.P. in activity A is greater than that in another activity, an optimum has not been reached. Now it would be profitable for the firm to shift labour from low-marginal value to high- marginal value uses.

This will surely raise the to­tal value of all products taken together. For exam­ple, if V.M.P. in activity A is Rs. 50 and that in ac­tivity B is Rs. 55, it will pay the firm to expand activity B and reduce activity A. The optimum is reached when V.M.P. is the same in all the five ac­tivities. In terms of symbol

VM P_LA = VMP_LB = … = VMP_LE

Here the subscript l denotes labour and the oth­er subscripts refer to the activities.

At this stage it is necessary to clarify three im­portant points:

(1) Firstly, the values of the marginal products in the above formula are net of incremental cost (the incremental costs, as we have noted, do not in­clude the cost of the input being allocated). But if one extra unit of labour is employed in activity A, physical output may increase by 100 units. Each unit may sell at Rs. 25 and the total revenue of the firm will rise by Rs. 2,500.

But in order to produce this output, some extra cost will have to be incurred because the increased production will consume raw- materials, fuel and other inputs. So the variable cost in activity A (not counting the labour cost) will be higher. If this extra cost is Rs. 1,500, the firm will be left with a net addition of Rs. 1,000. The value of the marginal product relevant for decision making purpose is Rs. 1,000.

If the revenues resulting from this extra product are to be obtained in future, it is necessary to apply the discounting principle. It is necessary to discount those revenues to compare the alternative activi­ties. Suppose activity B produces revenues immedi­ately, but activity C takes five years to generate any revenue at all.

So the discounting of those reve­nues is absolutely essential for making these activ­ities comparable. This sort of reasoning applies in capital budgeting which is concerned with alloca­tion of capital expenditure over time.

In order to derive an optimum return from investment the firm should apply the funds where the discounted val­ues of the marginal products are greatest, expand­ing the high-value activities and contracting the low value activities until a equality of marginal values is achieved.

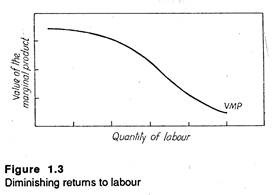
(2) So far we have implicitly assumed that there are diminishing returns to the inputs being allocated. As more and more units of the variable factor (here labour) are added in the production (fixed factor remaining unchanged) each extra unit of labour makes less and less extra contribution to the total product.

Fig 1.3 shows that as more labour is added to activity A, the marginal product of labour will diminish. This happens because each worker is gradually having less and less capital to work with.

(3) It may also be noted that in order to sell the extra product the firm may have to reduce the price of the product (if it operates in an imperfect­ly competitive market). In this case the value of marginal product (marginal physical product times the market price of the product — MPP x P) will diminish.

(4) Finally, one may refer to complementarity of demand: an increase in the availability of one product may stimulate the sales of another.

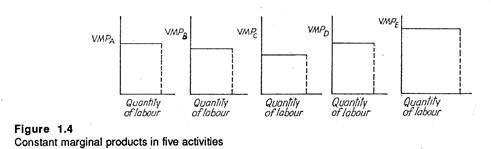
Constant Marginal Products:

In many real life situations the law of diminishing returns may not operate in the same way as described above. It is quite possible for a firm to increase the quantity of labour in one department without encountering diminishing marginal product until some limit of capacity is reached or until all the workers are em­ployed.

In this case we may expect the curve for the value of the marginal product to be horizontal up to full capacity, and then to drop to zero. Fig 1.4 illustrates such situation for five different activities.

In this situation the values of the marginal products are not equal in all activities unless there is surplus labour. Since the value of the marginal product is the highest in activity E, the company may prefer to employ all of the labour to E. How­ever, some constraint, such as a limit of the capaci­ty in E, or limits on other variable inputs required, will set a limit on the amount of labour that may be used in E.

The net result of our above discussion is this:

We may retain the equimarginal principle as long as diminishing returns operate at some stage of the production process; but when the values of the mar­ginal products are constant (horizontal) we make use of the following alternative principle:

We have to apply inputs first to activities with higher marginal product values before mov­ing to lower values.

The equimarginal principle can be applied in a variety of real life situations. We find its wide­spread use in budgeting the objective of which is to allocate resources where they are most productive.

But what is relevant for decision making is margi­nal productivity, not average productivity. Even when it is very difficult to measure productivity, we can apply the equimarginal principle in a rough or general way in order to avoid waste in useless ac­tivities.

We always find an application of this principle in any discussion of budgeting. We shall observe that whatever criterion is used in selecting a pro­ject, the goal is to isolate investments with high rates of return, from those with low rates of return so as to ensure optimum allocation of capital re­sources.

We also find an application of the principle in multiple product pricing.The equimarginal principle may also be ap­plied in allocating research expenditures. A profit- maximizing firm is likely to expand research ac­tivities that have started paying off and to contract activities that have reached (or likely to reach) their peak of usefulness.

Unless this com­parison is made expenditure is likely to be made on non-essential activities. In order to estimate the worth of alternative lines of research it is neces­sary to evaluate each research programme individ­ually.

Managerial Economics: Concept # 6.

The Contribution Concept:

The various concepts developed so far are inter­dependent. For example, in measuring opportunity cost of capital we use a discount factor by following the discounting principle. The same thing is true of the contribution concept.

Consider a simple product whose price is deter­mined either by the market forces the forces of demand and supply, or by some government agency like the Bureau of Costs and Industrial Prices (Govt, of India, New Delhi). Assume this price is Rs. 93.

The total cost including allocated over­heads is Rs. 105, but the incremental cost is only Rs. 74. The loss on the item seems to be Rs. 12. So at first sight the firm may think of dropping the product. However, if the contribution to overhead and profits is Rs. 19 = (Rs. 93 – Rs. 74), further anal­ysis is required before arriving at a decision.

It is not always worthwhile to retain a product simply because its contribution is positive. If the company is having a package of orders on products (say, B, C or D) requiring the same scarce resources per unit — production time or machine time and la­bour — and if these products make larger contribu­tions, viz., Rs. 50 or Rs. 40 or Rs. 30, there is no point in sacrificing these larger contribution in favour of product A.

However, what is important is the com­parison of contributions, not the comparison of prof­its or losses based on full costs.

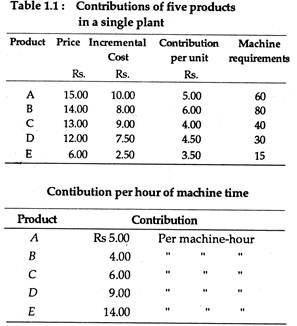
Suppose the only production constraint in a multi-product firm is machine-hours available. Now we can convert the contribution per unit of output into contributions per machine-hour. Table 1.1 il­lustrates such a situation in case of a company pro­ducing five products.

At first sight product B appears to be the best. Since its contribution is the highest, it deserves the top priority in allocation of capacity. But product B’s demand on capacity is also maximum. By con­verting the contributions into contributions per hour of machine time, we get the following results.

Now it is clear that the product E, which ini­tially appeared to be the least profitable, is now the largest contributor. Therefore, the principle should be almost the opposite to those that ap­peared at first glance.

If there are more constraints, i.e., more than one capacity bottleneck and all products pass through, say, four or five different processes, it will no long­er be possible to compute contributions in terms of one of the bottlenecks. We have to make use of lin­ear programming to reach an optimum solution (i.e., to choose an optimum product mix).

So long we assumed that demand for each prod­uct remained unchanged as also its price. Now sup­pose the quantity demanded of product E increases at a lower price. Now we can compare product E’s contribution of Rs. 2.50 at a price of Rs. 6 with its contribution of Rs. 3 at a price of Rs. 5.50.

If sales at a higher price are 8,000 units and at the lower pric­es 15,000 units, the total contribution from product E increases from Rs. 28,000 to Rs. 45,000. So, it is in the Tightness of things to accept the lower unit con­tribution to obtain the higher volume, even if other higher unit contribution products are sacrificed.

The contribution concept is often used in product- mix decisions, also in pricing decisions. It is also applicable in make or buy decisions. Finally, in a discussion on capital budgeting, it is usually discov­ered that the cash flows estimated by financial analysis are closely related to the contribution con­cept.

Managerial Economics: Concept # 7.

The Concept of Negotiation Principle:

Changes in costs and revenues, all commitments made in the short or long run, interest rates, net cash flows, the contribution margin that product E could (should) make to the overall profitability of company, are all negotiable.

In fact, everything in the real commercial world is negotiable, such as housing prices and terms and conditions of payment, equipment parts, specifications, and prices. Like­wise, a businessman contemplating merger, acquisi­tion, consolidation or other form of corporate take­over is always in a position to negotiate a deal depending on his bargaining strength.

In fact, each major commitment facing a firm can be negotiated. If a negotiation is successful both the parties are happy. An example of this is collective bar­gaining between the employer and the employee. An intelligent businessman must understand the process by which negotiation takes place.

Negotiations refer “to the part of coming to terms in as friendly a manner as possible with a party who represents interests that differ from one’s own.”

For example, if company A decides to own and operate company B, the management of B must be convinced that it is to B’s advantage, how­ever defined, to allow A to win. Clearly, if the transaction is to B’s interest, B has also to win. Such win-win situations are possible through nego­tiations.

In the absence of negotiation there may be a winner and a loser. In such an event, the winner may proceed one or two step(s) at most, but the en­tire process may also be started afresh.

For exam­ple, if labourers lose in a wage bargain, they are likely to oppose the wage contract sooner or later. A knowledge of the negotiation principle is im­portant because it is conducive to one’s business suc­cess. However, negotiation is a very challenging area of business activity.

Strategic Planning:

All the principles developed find their application in strategic planning which “re­views the economic impact of current micro and ma­cro events on the overall direction of a specific firm and considers alternative actions that could have been made and probable change in outcome that might have occurred as a result of those actions. Alternatively, those that appear promising are seriously considered for future use.”

Strategic planning involves three things:

1. Establishment of long-run objectives

2. Setting up short-run goals and

3. Designing specific strategies to reach the goals.

The whole process is logical and systematic. Each step has a purpose. In the words of Coyne, “In successfully applying economic principles to the price and output behaviours of a profitable corpo­ration, one must realize that short-run budgets and such things as deciding whether to put on the third shift as opposed to working the second shift overtime must be part of the overall strategic plan if the results of those decisions are to be meaningful to the firm.”

Strategic planning works like this:

1. The corporate planning manager or his team establishes an objective (which cannot be eas­ily defined and/or reached).

2 Goals are designed to reach the objective. These can be easily defined and reached, oth­erwise they are considered to be unrealistic and must be revised.

3. Strategies are established for achievement of those goals. The strategies must, of necessity, be realistic in terms of achievement.

As the strategies are implemented and goals are reached, it gradually becomes easier to achieve the objectives. However, since objectives are not precisely defined, it is difficult to know when they are achieved until the event actually occurs.

Product-line decisions:

With the framework of corporate objectives and goals, business firms face a number of problems: whether to add new products, drop old products, change the relative proportions of products, sell part of the product to other firms. These problems crop up in the short run when capacity is fixed.

Even in the short-run a firm is faced with a va­riety of problems. Let us consider a situation in which a firm has excess capacity. Its present line of products is unable to absorb its capacity fully. The question is whether to add a new product in the product line. Before taking any decision the firm has to determine and measure the contribution of the proposed product to overheads and profits.

This requires an estimate of the added revenue and added cost of the product. The decision criterion here is simple enough: if the contribution the difference between the added revenue and the in­cremental cost is positive, the product should be added to the existing product size.

However, there are certain other considerations as well:

(1) Firstly, if an even better new product is available, the proposed product should not be in­troduced.

(2) Secondly, there is need to search out all the available opportunities before making the final decision. In other words, there is need to esti­mate the opportunity costs of alternative uses of the excess capacity.

It may be noted that the op­portunity cost of decision means sacrificing alterna­tives. For example, the opportunity cost of using a machine to produce one product (say X) is the sacri­fice of earnings that would be possible from other products (Y, Z, etc.).

Therefore, the opportunity cost of using a machine that is useless for any product (say X) is zero, since its use requires no sacrifice of other opportunities. In a like manner, the opportu­nity cost of using idle space is obviously less than that of using space needed for other activities.

So opportunity costs require the measurement of sacrifices. And any decision regarding product sub­stitutions is made on the basis of this concept. For example, the expenditure on raw-materials in­volves a sacrifice of other possible expenditures and is thus an opportunity cost. In the words of T.J. Coyne, “the only costs relevant for decision making are opportunity costs.”

Another factor is the possible impact of new product on the existing products. In some cases, the new product may be a complement for, rather than a substitute, of the old product.

In other words, “the new product may complement or round out the product line, increasing the sale of the other prod­ucts. In such a case, the contribution to overhead and profits of the new product is greater than the contribution to overhead and profit of the new product itself.”

There are also instances where the product may compete with items in the existing line so that the initial contribution estimates are to be revised downward.

Such adjustments in esti­mates should take into account both short-term and long-term impacts of the new product: for example whether the new product can be abandoned when demand for the other products recovers or whether an expansion of facilities will be justified.

In most situations, it is preferable to accept temporary ex­cess capacity than to create production bottlenecks when the excess capacity disappears. Moreover, management has also to consider whether it has the necessary know-how and skill to produce and distribute the new product. If the situation is one of full use of capacity, the problem becomes even more complicated.

In this situation an optimal use of its resources demands that the management not only determine the con­tribution of each product (and of products that might be introduced in the product mix) but also de­termine how much of the opportunity cost of in­creasing the output of one product is in terms of the reduction of the contributions of other products.

A Textbook Example:

In his famous title:

Managerial Economics, Coyne considers a more complex situation, which has relevance to the real world: the allocation of scarce resource to a variety of slowly maturing products. He cites the example of garden nursery with a fixed plot of land and a wide variety of planting opportunities.

The owner of the nursery faces the problem of determining which plants to propagate and grow, what ages to assume in mak­ing such choices, what futures to assume and how to fix prices on mature plants. Moreover, the decision maker must determine when to reduce prices on plants so that they can be sold out quickly and land tied up in them can be released for other (and more profitable) uses.

The solution to this problem re­quires a comparative evaluation (or estimate) of the contributions of various plants over time, which, in its turn, requires:

(1) Separate estimates of revenues and incremental costs and

(2) The discount­ing of future revenues, costs and contributions to find out the present value of such contributions at the time of making decisions on the use of the land.

True enough, “estimates of the present value of the contribution of all plants on an acre basis would provide basis for rational decisions. These esti­mates would make it possible to compare the con­tribution from rapidly maturing plants with those of slowly maturing plants.”

Other applications of Managerial Economics:

The following two situa­tions maybe considered:

(a) Decision on allocation of space in a retail store:

Limited floor space may be allocated among various products on the basis of their relative con­tribution to overhead and profit above incremental cost.

(b) Decisions on advertising expenditures:

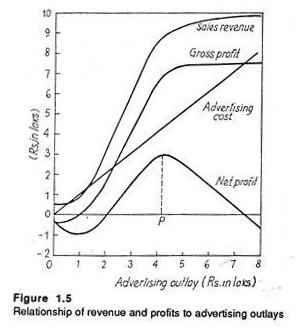
In or­der to determine the optimum advertising budget it becomes necessary for a firm to measure the respon­siveness of sales to advertising, along with meas­ures of the added cost of production of a larger vol­ume

Fig. 1.5 illustrates how sales and profits would respond to increased advertising outlays.

Since advertising has a lagged effect it is very difficult to measure its effectiveness on sales reve­nue or turnover. However, the principles may be used to assess the true worth of advertising.