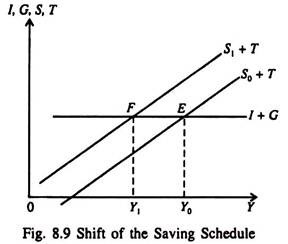
Let’s consider the effect of an increase in the desire to save. This is shown by an upward shift in the S + T function to S1 + T in Fig. 8.9. At any given level of income people now want to save more than before.
At the initial equilibrium level of income Y0, with the new saving function, S + T exceeds planned I̅ + G which results in an unintended increase in inventories of Δ inv0.
As we have seen, this will cause producers to cut production until Δ inv is zero, where Y reaches a new equilibrium at Y1, which brings a return to the original level of saving, but at a lower level of income. Thus, in a situation where I̅ + G is fixed exogenously, an exogenous increase in the desire to save leads to an unchanged level of S + T but at a lower level of income. Income must fall to reduce saving enough to restore equilibrium S + T = I̅ + G with the higher saving function.
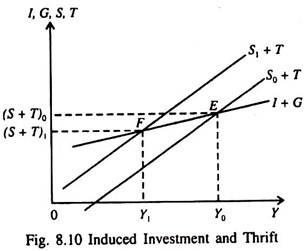
If we change the assumption that I and G are fixed independently of Y, we can observe the possibility of what has been called the paradox of thrift. Suppose that, as shown in Fig. 8.10, I + G is an increasing function of income. That is, as the level of income increases, planned investment and/or government purchases rise. This gives the I̅ + G line a positive slope in Fig. 8.10.
ADVERTISEMENTS:
Now we can see that an autonomous shift upward in saving to S1 + T causes not only a decrease in the level of income from Y0 to Y1, but also brings a decrease in the level of realised S + T. Thus, we have the result that an increased desire to save can lead ultimately to a fall in the actual level of S + T since the drop in income reduces planned investment. This is the so-called paradox of thrift.