3 Methods For Measuring Elasticity Of Demand – Explained!

The following three methods are usually used by the economists for measuring it:

(i) Total Expenditure Method,

(ii) Proportional Method,

(iii) Geometrical Method.

Total Expenditure Method:

Under this method, we measure elasticity of demand by examining the change in the total expenditure due to a change in price.

Look at the following demand schedule relating to handkerchiefs:

Unity Elasticity:

When the total amount of money spent remains the same (e.g., between Nos. 2 and 3 above), the elasticity is said to be unity.

Greater Than Unity:

When the total amount of money spent increases with a fall in price (or decreases with a rise in price), the elasticity is said to be greater than unity (as between the two prices Nos. 3 and 4).

Less than Unity:

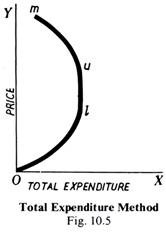
When the total amount of money spent decreases with a fall in price (or increases with a rise in price), the elasticity is said to be less than unity (e.g., between the two prices Nos. 1 and 2). We can also represent this method diagrammatically (Fig. 10.5). Take total expenditure along the X-axis and price along the Y-axis. We get a backward bending curve Olum. The portion O1 represents less than unity elasticity, because an increase or decrease in price increases or decreases the total expenditure.

The portion um represents unity elasticity because a change in price has got no effect on total expenditure; it remains the same. Portion um represents more than unity elasticity because an increase in price decreases the total expenditure and a decrease in price increases the total expenditure.

Proportional Method:

Under this method, we measure elasticity by comparing the percentage in price with the percentage change in demand. The elasticity of demand is unity, greater than unity, or less than unity, according as the change in demand is proportionate, more than proportionate, or less than proportionate to the change in price respectively. The elasticity is the ratio of the percentage change in the quantity demanded to the percentage change in the price charged.

The formula is:

Elasticity = Proportionate change in demand/ Proportionate change in price

= Change in Demand/ Amount demanded + Change in price/ Price

This formula will be better understood with the help of mathematical illustration.

Suppose mangoes are selling at the price 25 P. each and a consumer demands 10 mangoes at this price. If the price falls to 20 P. each and the consumer now demands 15 mangoes, find out his elasticity of demand for mangoes.

According to the above formula:

15—10/10 ÷ 25—20/25

= 5/10 ÷ 5/25

= 5/10 × 25/5

= 25/10 = 2.5

In other words, the elasticity of demand of our hypothetical consumer for mangoes is high; it is much greater than unity (2.5).

Let us now take an example of low elasticity.

Suppose that the demand for common salt is 5 kilogram per month at the price of 20 P. per kg. Now suppose that its price is doubled, i.e., it rises to 40 P. per kg. and now only 4 kg. are demanded.

According to our above formula:

Elasticity = 5-4/5 ÷ 40/-20/20

= 1/5 ÷ 20/20

= 1/5 × 1/1

= 1/5

In other words, elasticity of demand is very low and is less than unity. In regard to this proportional method, we can broadly say that when the percentage change in price and the consequent percentage change in demand are equal, elasticity will be unity; when the percentage change in demand is greater than that in price, elasticity will be greater than unity and, conversely, elasticity will be less than unity when the percentage change in demand is less than that in price.

Geometrical Method: Point Elasticity:

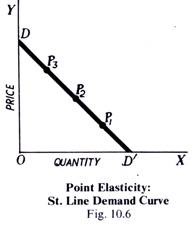
This method is used to measure the elasticity of demand at any given point on the demand curve. Look at Fig. 10.6

DD’ is the straight-line demand curve. Elasticity is represented by the fraction: distance from D’ to the point on the curve divided by the distance from the other end to that point.

Thus, elasticity of demand on the points P i, Pi, and P₁ is respectively.

D’P₁ D’P₂/DP1 DP2 and D’P₃/DP₃

If P₂, is the middle point of DD’, then elasticity at P₂, will be

D P₂, = 1,(D’P₂, being equal to DP,)

i.e., elasticity at P₂, the middle point, is unity. At any point lower than P₂, elasticity will be less than unity and at any point above P₂, it will be greater than unity.

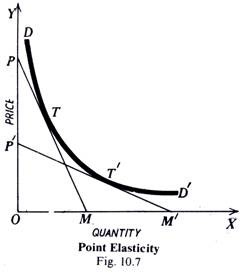
Even if the demand curve is not a straight line, the above formula will apply. A tangent will, however, have to be drawn at the point on the curve where elasticity is to be measured. It is illustrated in the diagram (Fig. 10.7) given on the previous page.

DD’ is the demand curve, and two tangents PM and P’M’ are drawn respectively at the points T and T’ At point T, elasticity will be equal to TM/PT. This will apply only so long as the tangent and the curve coincides, which means for an infinitesimally short distance. If there is any departure from point T, a new tangent will have to be drawn and elasticity ascertained accordingly. At point T’ elasticity = M/P’ T’/T. Clearly, elasticity at T is greater than elasticity at T’.

Slope and Elasticity Distinguished:

This slope of the curve is not to be confused with elasticity. The steepness of the curve is no indication of the extent of elasticity.

In the diagram 10.6, the demand curve DD’ has the same steepness but different elasticity’s at different points. If elasticity and slope were closely related, the elasticity would be constant throughout. But it is not so. The demand is elastic near the price-axis (OY), say, near the point D, and unitary half way, i.e., at point P₂, and inelastic near the quantity-axis, i.e., near D’. Since elasticity depends not an absolute change but no percentage changes, it really depends on the steepness of the curve relative to the price-quantity ratio.

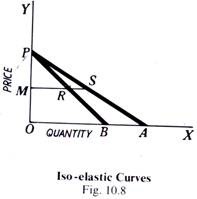
In Fig. 10.8, the curves BP and AP have different slopes but they have the same elasticity at a given price. Let OM be the price. Draw a straight line parallel to X-axis cutting BP at R and AP at S. Now elasticity of the curve BP at the point R is

BR/RP

The elasticity of the curve at the point S is AS/SP.

Now in the right-angled triangle BQP,

BR/OM RP/MP

But in the right -tangled triangle AOP,

OM/AS = MP/SP

BR/AS = RP/SP

That is, elasticity at both R and S is the same even though the two curves have different slopes. Such curves are called iso-elastic.

Thus elasticity of demand is not indicated by the slope of the curve as is generally supposed. Elasticity of demand is always at a price. Different points on the- demand curve have different elasticity’s of demand. By merely seeing the slope of the demand curve, therefore, we cannot say that the demand is less elastic or more elastic. Again, it is possible to draw a curve which may throughout its length represent unit (i.e., same) elasticity even though it may have different slopes. This curve is known as a Rectangular Hyperbola.

Income Elasticity of Demand:

Elasticity of demand means the price elasticity of demand. As already pointed out, income elasticity of demand must be clearly distinguished from the price elasticity of demand. Whereas the price elasticity of demand refers to the change in quantity demanded as a result of change in price, the income elasticity of demand means the change in demand which occurs as a result of change in income.

Thus income elasticity of demand may be defined as:

Proportionate change in the quantity purchased/ Proportionate change in income while price remains constant. Generally speaking, when our income increases, we desire to purchase- more of the things than we were previously purchasing, unless the commodity happens to be an “inferior” one.

Normally, then since the income effect is positive, income elasticity of demand is also positive. It is zero when change in income makes no change to our purchases and it is negative when with an increase in income, the consumer purchases less, e.g., in the case of inferior goods.

Cross Elasticity of Demand:

There is another concept of elasticity of demand which is called cross elasticity of demand. Cross elasticity of demand refers to the change in demand for a good as a result of change in the price of another goods. Proportionate change in quantity demanded of X /Proportionate change in the price of Y Cross elasticity of demand arises in cases of inter-related goods, such as substitutes and complementary goods.

Importance of the Concept of Elasticity of Demand:

The concept of elasticity of demand has great practical importance:

For Businessmen and Monopolists:

It guides the businessman in fixing the prices of his goods. If the demand for a commodity is inelastic, he knows that the people must buy it whatever be the price. In such cases, he will be able to raise the price. If he is a monopolist he will certainly do so and earn a larger ne’ Profit. When the demand is elastic, a small fall in price will increase the sales and bring more profit.

For the Finance Minister:

The Finance Minister also takes note of elasticity of demand when selecting commodities for taxation. In case he wants to be certain of the revenue, he taxes those commodities for which the demand is inelastic. People must continue buying them even though the prices rise with the tax. If the demand is elastic, people will buy less of them and the Government would get less revenue.

Joint Products:

In case of joint products, separate costs of production of the two commodities are not ascertainable. In such cases, price of each will depend on the elasticity of demand of each. The transport authorities also fix the prices of the various services they sell, after considering their elasticity of demand for the respective services.

In Industrial Production:

The volume of industrial output depends on the nature of demand. If the demand is elastic, by slightly reducing the price, sales can be increased, and the output too will increase.

Paradox of Poverty in Plenty:

The concept of elasticity can explain how the farmers may remain poor even when there is a bumper crop. If the elasticity of demand for wheat is unity, the incomes of the growers would remain the same whatever the condition of the crop. In a year of bad harvest the rise in price would compensate for reduced output and in a year of good crop, the price will fall and thus reduce the income.

Determination of Wages:

Elasticity can also influence wages. If demand for a particular type of labour is inelastic, it can succeed in raising wages.

In International Trade:

The concept of elasticity of demand is of great significance in international trade also. That country will benefit the most from international trade the demand for whose imports is very elastic, but that for exports is inelastic. The present position in respect of India’s exports and imports is the reverse of it because her demand for imports of crude oil and machinery, etc., is more or less inelastic, while the foreign countries’ demand for exports from India is quite elastic. India, therefore, is unable to benefit from her international trade as much as many of her trading partners do from their trade with India. Thus, the concept of elasticity has great practical importance in the various fields of applied Economics.