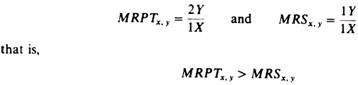Social Welfare (6 Major Criteria)

To evaluate alternative economic situations we need some criterion of social well- being or welfare.

The measurement of social welfare requires some ethical standard and interpersonal comparisons, both of which involve subjective value judgements.

Objective comparisons and judgements of the deservingness or worthiness of differ­ent individuals are virtually impossible. Various criteria of social welfare have been suggested by economists at different times.

1. Growth of GNP as A Criterion of Welfare:

Adam Smith implicitly accepted the growth of the wealth of a society, that is, the growth of the gross national product, as a welfare criterion. He believed that eco­nomic growth resulted in the increase of social welfare because growth increased em­ployment and the goods available for consumption to the community. To Adam Smith, economic growth meant bringing W closer to W*.

The growth criterion implies acceptance of the status quo of income distribution as ‘ethical’ or ‘just’. Furthermore, growth may lead to a reduction in social welfare, depending on who avails mostly from it. However the growth criterion highlights the importance of efficiency in social welfare. Given that social welfare depends on the amount of goods and services (as well as on their distribution) efficiency is a neces­sary prerequisite for the maximisation of the level of welfare.

We note here that economic efficiency can be defined objectively, and the modern welfare economics is mainly concerned with the examination (comparison) of the (Pareto)-efficiency of different economic situations. However, efficiency, although a necessary condition, is not sufficient to guarantee the maximisation of social welfare. Efficiency does not dispose of the need of having an ethical standard of comparing alternative economic states.

2. Bentham’s Criterion:

Jeremy Bentham, an English economist, argued that welfare is improved when ‘the greatest good (is secured) for the greatest number’. Implicit in this dictum is the assumption that the total welfare is the sum of the utilities of the individuals of the society. The application of Bentham’s ethical system to economics has serious short­comings. To illustrate the pitfalls in Bentham’s criterion let us assume that the society consists of three individuals, A, B, and C, so that

W = U_A + U_B + U_C

According to Bentham ΔW > 0 if (ΔU_A + ΔU_B + ΔU_C) > 0. However, assume that the change which resulted in the changes in the individual utilities is such, that A’s and B’s utility increases, while Cs utility decreases, but (∆U_A + ∆U_B) > |∆U_C|. In other words, two individuals are better-off while the third is worse-off after the change has taken place, but the sum of the increases in utilities of A and B is greater than the decrease in the utility of C.

Bentham’s criterion, obviously, implies that A and B have a greater ‘worthiness’ than C. That is, implicit in Bentham’s criterion is an interpersonal comparison of the deservingness of the members of the society. There is another difficulty with the application of Bentham’s criterion.

This criterion cannot be applied to compare situations where ‘the greatest good’ and the ‘greatest numbers’ do not exist simultan­eously. For example assume that in a situation U_A = 200, U_B = 50, U_C = 30, so that the total utility in the society is 280. In another situation assume that a change occurred and U_A = 100, U_B = 80, and U_C = 80, so that the total utility is 260. The first situation has ‘the greatest good’ (280 > 260), but the second involves a more even distribution (of a smaller ‘total good’) among the ‘greatest number’.

3. A ‘Cardinalist’ Criterion:

Several economists proposed the use of the ‘law of diminishing marginal utility’ as a criterion of welfare. Their argument can be illustrated by the following example. Assume that the society consists of three individuals; A has an income of £1000, while B and C have an income of £500 each. Consumer A can buy double quantities of goods as compared to B and C.

However, given the law of diminishing marginal utility, A’s total utility is less than double the total utility of either B or C, because A’s marginal utility of money is less than that of B or C. Thus W < W*. To increase social welfare income should be redistributed among the three individuals. In fact cardinal welfare theorists would maintain that social welfare would be maximised if income was equally distributed to all members of the society.

The cardinalist approach to welfare has a serious flaw: it assumes that all indivi­duals have identical utility functions for money, so that with an equal income distrib­ution all would have the same marginal utility of money. This assumption is too strong. Individuals differ in their attitudes towards money. A rich person may have a utility for money function that lies far above the utility (for money) function of poorer individuals.

In this case a redistribution of income (towards more equality) might reduce total welfare. Opponents of the cardinalist approach pointed out also that welfare effects of an equal distribution of income cannot be examined in isola­tion from the effects on resource allocation (which would follow the redistribution of income) and the incentives for work of the various individuals.

An equal income distribution may induce some people to work less, thus leading to a reduction in total GNP. Similarly, equal incomes in all employments may lead to an allocation of resources which produces a smaller total output. In both cases income equality results in (Pareto) inefficiency in the use of resources and a reduction in social welfare.

4. The Pareto-Optimality Criterion:

This criterion refers to economic efficiency which can be objectively measured. It is called Pareto criterion after the famous Italian economist Vilfredo Pareto (1848-1923). According to this criterion any change that makes at least one indivi­dual better-off and no one worse-off is an improvement in social welfare. Conversely, a change that makes no one better-off and at least one worse-off is a decrease in social welfare. The criterion can be stated in a somewhat different way: a situation in which it is impossible to make anyone better-off without making someone worse-off is said to be Pareto-optimal or Pareto-efficient.

For the attainment of a Pareto-efficient situation in an economy three marginal conditions must be satisfied:

(a) Efficiency of distribution of commodities among consumers (efficiency in exchange);

(b) Efficiency of the allocation of factors among firms (efficiency of production);

(c) Efficiency in the allocation of factors among commodities (efficiency in the product-mix, or composition of output).

Before exa­mining these marginal conditions we discuss briefly the main weaknesses of the Pareto criterion. The Pareto criterion cannot evaluate a change that makes some individuals better- off and others worse-off. Since most government policies involve changes that benefit some and harm others it is obvious that the strict Pareto criterion is of limited applicability in real-world situations.

Furthermore, a Pareto-optimal situation does not guarantee the maximisation of the social welfare.For example, we know that any pointon the produc­tion possibility curve represents a Pareto-efficient situation. To decide which of these points yields maximum social welfare we need an interpersonal comparison of the individual consumer’s utility. We will show that the Pareto- optimal state is a necessary but not sufficient condition for maximum social welfare.

Let us examine now the three marginal conditions that must be satisfied in order to attain a Pareto-efficient situation in the economy.

(a) Efficiency of distribution of commodities among consumers:

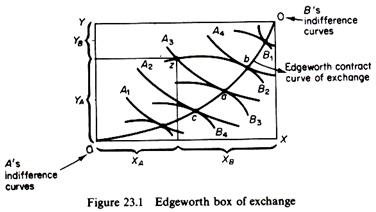
Applying the Pareto optimality criterion to the case of distribution of commodities Y and X, we can say that a distribution of the given commodities X and Y between the two consumers is efficient if it is impossible by a redistribution of these goods to increase the utility of one individual without reducing the utility of the other. In figure 23.1 we show the Edge-worth box for the given commodities X and Y.

We know that only points on the Edge-worth contract curve satisfy the Pareto-optimality condition. Any other distribution off the contract curve is inefficient. For example, point z is inefficient, since a redistribution of the commodi­ties such as to reach any point between a and b increases the utility of both con­sumers. A movement to a increases the utility of B without reducing the utility of A.

Similarly, the distribution implied by b increases the utility of A without reducing the utility of B. Thus all the points from a to b represent improvements in social welfare compared with the distribution at z. By reversing the argument it can be seen that a movement from a point on the contract curve to a point off it results in a decrease in social welfare.

Thus the contract curve shows the locus of Pareto-optimal or -efficient distribution of goods between consumers. This curve is formed from the points of tangency of the two consumers’ indifference curves, that is, points where the slopes of the indifference curves are equal. In other words, at each point of the contract curve the following condition is satisfied

MRS^A_x,_y = MRS^B_x,_y

Therefore we may state the marginal condition for a Pareto-efficient distribution of given commodities as follows:

The marginal condition for a Pareto-optimal or -efficient distribution of commodities among consumers requires that the MRS between two goods be equal for all consumers.

(b) Efficiency of allocation of factors among firm-producers:

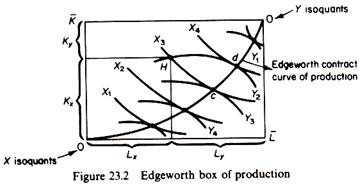
To derive the marginal condition for a Pareto-optimal allocation of factors among producers we use an argument closely analogous to the one used for the derivation of the marginal condition for optimal distribution of commodities among consumers. In the case of allocation of given resources K and L we use the Edge-worth box of production which is shown in figure 23.2.

Only points on the contract curve of production are Pareto-efficient. Point H is inefficient, since a reallocation of the given K and L between the producers of X and Y such as to reach any point from c to d inclusive results in the increase of at least one commodity without a reduction in the other. The contract curve is the locus of points of tangency of the isoquants of the two firms which produce X and Y, that is, points where the slopes of the isoquants are equal. Thus at each point of the contract curve the following condition holds

MRS^x_L,_K = MRS^Y_L,K

Therefore we may state the marginal condition for a Pareto-optimal allocation of factors among firms as follows:

The marginal condition for a Pareto-optimal allocation of factors (inputs) requires that the MRTS between labour and capital be equal for all commodities produced by different firms.

(c) Efficiency in the composition of output (product-mix):

The third possible way of increasing social welfare is a change in the product-mix. To define the third marginal condition of a Pareto-optimal state in an economy we will use the production possibility curve. Recall that the slope of the PPC is called the ‘marginal rate of (product) transformation’ (MRPT_x,y), and it shows the amount of Y that must be sacrificed in order to obtain an additional unit of X. In other words the MRPT is the rate at which a good can be transformed into another. The marginal condition for a Pareto-optimal or -efficient composition of output re­quires that the MRPT between any two commodities be equal to the MRS between the same two goods:

MRPT_xy = MRS^A_x,_y = MRS^B_x,_y

Since the MRPT shows the rate at which a good can be transformed into another (on the production side), and the MRS shows the rate at which consumers are willing to exchange a good for another, the rates must be equal for a Pareto-optimal situation to be attained. Suppose that these rates are unequal. For example assume

The above inequality shows that the economy can produce two units of Y by sacrificing one unit of X, while the consumers are willing to exchange one unit of Y for one unit of X. Clearly the economy produces too much of X and too little of Y relatively to the tastes of consumers. Welfare therefore can be increased by increasing the production of Y and decreasing the production of X.

In summary. A Pareto-optimal state in the economy can be attained if the follow­ing three marginal conditions are fulfilled:

1. The MRS_X,y between any two goods be equal for all consumers.

2. The MRTS_L,K between any two inputs be equal in the production of all commodities.

3. The MRPT_x,y be equal to the MRS_xy for any two goods.

A situation may be Pareto-optimal without maximising social welfare. However, welfare maximisation is attained only at a situation that is Pareto-optimal. In other words, Pareto optimality is a necessary but not sufficient condition for welfare maxi­misation. All points on the PPC are Pareto-optimal. The choice among these alterna­tive Pareto-optimal states requires some measure or criterion of social welfare.

5. The Kaldor-Hicks ‘compensation criterion’:

Nicholas Kaldor and John Hicks suggested the following approach to establish­ing a welfare criterion.

Assume that a change in the economy is being considered, which will benefit some (‘gainers’) and hurt others (‘losers’). One can ask the ‘gainers’ how much money they would be prepared to pay in order to have the change, and the ‘losers’ how much money they would be prepared to pay in order to prevent the change.

If the amount of money of the ‘gainers’ is greater than the amount of the ‘losers’, the change constitutes an improvement in social welfare, because the ‘gainers’ could compensate the ‘losers’ and still have some ‘net gain’. Thus, the Kaldor-Hicks ‘compensation criterion’ states that a change constitutes an improvement in social welfare if those who benefit from it could compensate those who are hurt, and still be left with some ‘net gain’.

The Kaldor-Hicks criterion evaluates alternative situations on the basis of mon­etary valuations of different persons. Thus it implicitly assumes that the marginal utility of money is the same for all the individuals in the society. Given that the income distribution is unequal in the real world, this assumption is absurd.

Assume, for example, that the economy consists of two individuals, A, who is a millionaire, and B, who has an income of £4000. Suppose that the change (being considered by the government) will benefit A, who is willing to pay £2000 for this change to happen, while it will hurt B, who is prepared to pay £1000 to prevent the change.

According to the Kaldor-Hicks criterion the change will increase the social welfare (since the ‘net gain’ to A, after he compensates B, is £1000). However, the gain of £2000 gives very little additional utility to millionaire A, while the ‘loss’ of £1000 will decrease a lot the well-being of B, who has a much greater marginal utility of money than A.

Thus the total welfare will be reduced if the change takes place. Only if the marginal utility of money is equal for all the individuals would the Kaldor-Hicks criterion be a ‘correct’ welfare measure. This criterion ignores the existing income distribution. In fact this criterion makes implicit interpersonal comparisons, since it assumes that the same amounts of money have the same utility for individuals with different incomes.

6. The Bergson criterion: the social welfare function:

The various welfare criteria so far discussed show that when a change in the economy benefits some individuals and hurts others it is impossible to evaluate it without making some value judgement about the deservingness of the different indi­viduals or groups. Bergson suggested the use of an explicit set of value judgements in the form of a social welfare function.

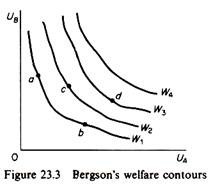
A social welfare function is analogous to the individual consumer’s utility function. It provides a ranking of alternative states (situations, configurations) in which different individuals enjoy different utility levels. If the economy consists of two individuals the social welfare function could be presented by a set of social indifference contours (in utility space) like the ones shown in figure 23.3. Each curve is the locus of combinations of utilities of A and B which yield the same level of social welfare.

The further to the right a social indifference contour is, the higher the level of social welfare will be. With such a set of social indifference contours alternative states in the economy can be unambiguously eval­uated. For example a change which would move the society from point b to point c (or d) increases the social welfare. A change moving the society from a to b leaves the level of social welfare unaltered.

The problem with the social welfare function is that there is no easy method of constructing it. Its existence is axiomatically assumed in welfare economics (see below). Somebody in the economy must undertake the task of comparing the various individuals or groups and rank them according to what he thinks their worthiness is.

A democratically elected government could be assumed to make such value judge­ments which would be acceptable by the society as a whole. This is implicitly or explicitly assumed when use is made of the apparatus of the social welfare function.

It should be noted that the social welfare function cannot be used to derive social (or community) indifference curves in output space (analogous to the indifference curves of a single individual) without taking into account the distribution of income among the various individuals in the economy.