Welfare Maximisation and Perfect Competition (With Diagram)

Under certain assumptions an economy can reach the point of maximum social welfare.

It should be stressed that the bliss point (and the solution of the system for the values of the ten variables that are the unknowns in the welfare-maximisation problem of the 2 x 2 x 2 model) depends only on techno­logical relations the problem of welfare maximisation is purely ‘technocratic’.

Recall that the bliss point is attained by equalising the slopes of isoquants, the slopes of the indifference curves, and the slope of the production possibility curve to the (equalized) slope of the indifference curves. Thus, the welfare-maximising solu­tion does not depend on prices.

Perfect competition can lead to a general equilibrium situation where the three marginal conditions of Pareto optimality are satisfied.

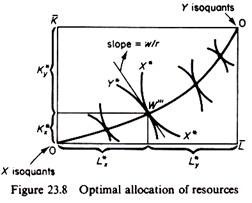
(a) Profit maximisation by the individual firm implies that whatever output the firm may choose as the most profitable must be produced at a minimum cost. Cost minimisation is attained if the firm chooses the input combination at which the marginal rate of technical substitution of the two factors is equal to the input price ratio.

MRTS_L,_k = w/r

Since in perfect competition all firms are faced by the same set of factor prices, it follows that

MRTS^x_L,_K = MRTS^y_L,_K = w/r

Thus in figure 23.8 the slope of the contract curve at W'” must be equal to w/r in perfectly competitive input markets, since W'” is the point of the (equalised) slope of the isoquants Y* and X*.

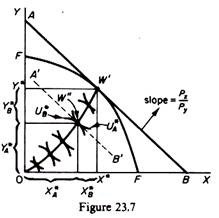
(b) Utility maximisation by each individual requires the choice of the product-mix where the marginal rate of substitution of the two commodities is equal to the ratio of their price

MRS_x,y = P_x/P_y

Since in perfect competition all consumers are faced by the same commodity prices, it follows that

MRS^A_x,y = MRS^B_x,y = P_x/P_y

Thus in figure 23.7 the slope of the contract curve at W” must be equal to the P_x/P_y ratio in perfectly competitive commodity markets, since W” is the point of the (equalised) slope of the indifference curves of the two consumers.

(c) We have shown that at the bliss point the (equalised) slope of the indifference curves (the ‘common’ MRS_x,y) is equal to the slope of the production possibility curve at W”. Thus at W”, which defines the product-mix that maximises social welfare, we have

MRPT_x,_y = P_x/P_y

(d) Finally, a firm in a perfectly competitive market maximises its profit by setting its marginal cost equal to the market price of the commodity. Consequently we have

MRPT_x,_y = P_x/P_y = MC_x/MC_y

Thus we have established that a perfectly competitive system guarantees the attainment of maximum social welfare. This is the result of the maximising behaviour of firms and consumers. In a perfectly competitive (free enterprise) system, each individual, in pursuing his own self-interest, is led by an ‘invisible hand’ to a course of action that increases the general welfare of all.

However, perfect competition is only one way for attaining welfare maximisation. A decentralised socialist system, for example, in which the government has somehow estimated ‘shadow’ prices and directs its individual economic units to maximise their ‘gains’, can in principle achieve the same results as a perfectly competitive system.

In summary, Implicit in the purely ‘technocratic’ problem of welfare maximisation is a set of ‘prices’. Decentralised decisions in response to these ‘prices’ by atomistic profit maximisers and utility maximisers will result in just that levels of inputs, outputs and commodity-distribution that the bliss point requires.

The individual maximisers can be acting in a perfectly competitive system, or in a decentralised social system of the Lerner-Lange type, where bureaucrats have established somehow the ‘prices’ that maximise social welfare and coerce the citizens to act in response to these ‘prices’.

The above ‘duality theorem’ is the kernel of modern welfare economics. This ‘dua­lity theorem’ may be stated as follows. Welfare maximisation can be attained by maximising behaviour of individuals, given the technological relations of the produc­tion function, ordinal indexes of the utility of consumers, and given a social welfare function. The welfare maximisation is independent of prices.

However, implicit in the logic of this purely technocratic formulation is a set of constants. These constants can be the prices of a perfectly competitive economy, or the ‘shadow prices’ of a socialist economy. Thus, if these ‘prices’ (constants) are known (as, for example, the prices of a perfectly competitive system), and individual profit maximisers and utility maxi- misers act in response to these prices, their behaviour will lead to the maximisation of social welfare.