The Classical Theory of Employment (With Diagram)

Let us make an in-depth study of the Classical Theory of Employment.

Introduction to the Classical Theory:

The classical theory assumes over the long period the existence of full employment without inflation.

Given wage-price flexibility, there are automatic competitive forces in the economic system that tend to maintain full employment, and make the economy produce output at that level in the long run.

Thus, full employment is regarded as a normal situation and any deviation from this level is something abnormal since competition automatically pushes the economy toward full employment.

The classical theory of income, output and employment is based on the following assumptions:

1. There is a normal situation of full employment without inflation.

2. There is a laissez faire capitalist economy without foreign trade.

3. There is perfect competition in labour, money and product markets.

4. Labour is homogeneous.

5. Total output of the economy is divided between consumption and investment expenditures.

6. The quantity of money is given. Money is only a medium of exchange.

7. Wages and prices are flexible.

8. Money wages and real wages are directly related and this relationship is proportional.

9. Capital stock and technological knowledge are given in the short run.

Now we study the three pillars of classical theory.

Say’s Law of Markets:

Say’s Law of Markets is the core of the classical theory of employment. Jean Baptiste Say, an early 19th century French Economist gave the proposition that “supply creates its own demand.” This is known as Say’s Law. In Say’s own words, “It is production which creates markets for goods. A product is no sooner created than it, from that instant, affords a market for other products to the full extent of its own value. Nothing is more favourable to the demand of one product, than the supply of another.”

In its original form, the law was applicable to a barter economy where goods are ultimately sold for goods. Every good brought to the market creates a demand for some other goods. Say argued that since work is unpleasant, no person will work to make a product unless he wants to exchange it for some other product which he desires.

Therefore, the very act of supplying goods by a large number of small producers implies a demand for them from producers of other goods. In each a situation there cannot be general over-production because supply of goods will not exceed demand as a whole.

Classical conceded that particular good may be overproduced because the producer incorrectly estimates the quantity of the product which others want. But this is a temporary phenomenon for the excess production of particular product can be corrected in time by reducing its production.

Even after a hundred years, James Mill supported Say’s Law in these words, “Consumption is co­extensive with production and production is the cause, and the sole cause of demand. It never furnishes supply without furnishing demand, both at the same time and both to an equal extent…. whatever the amount of annual produce; it can never exceed the amount of annual demand.”

Thus supply creates its own demand and there cannot be general overproduction and hence general unemployment.

The classical logic was that existence of money does not alter the working of the basic law. “Say’s law, in a very broad way, is,” as Professor Hansen has said, “a description of a free-exchange economy. So conceived, it illuminates the truth that the main source of demand is the flow of factor income generated from the process of production itself. When producers obtain the various inputs (land, labour and capital) to be used in the production process, they generate the necessary income accruing to the factor owners in the form of rent, wages and interest.

This, in turn, causes adequate demand for the goods produced. In this way, supply creates its own demand. This reasoning is based on the assumption that all income earned by the factor-owners is automatically spent in buying commodities which they help to produce.

Classical further maintained that what is not consumed is saved and that all saving out of income is automatically invested through the capital market. Thus, in a state of equilibrium saving must equal investment. If there is any divergence between the two, the equality is maintained through the mechanism of the rate of interest. To the classicists, interest is a reward for saving.

The higher is the rate of interest, the higher the savings, and vice versa. On the contrary, the lower the rate of interest, the higher the demand for investment funds, and vice versa. If at any given time, investment exceeds saving, the rate of interest would rise.

Saving would increase and investment would decline till the two are equal at the full employment level. This is because saving is regarded as an increasing function of the interest rate and investment a decreasing function of the rate of interest. This helps establish the equilibrium condition of saving-investment equality.

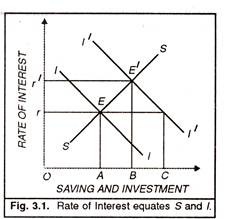
The process of generation of the equality between saving and investment is shown in Figure 3.1 where SS is the saving curve and II is the investment curve. The two curves intersect at E where the rate of interest gets determined at the level of Or and both saving and investment are equal to OA. If there is an increase in investment, the investment curve shifts to the right and is shown as IT curve.

At the interest rate Or, investment is greater than saving. According to the classical economists, the saving curve SS remains at its original level when there is any increase in investment. To maintain the equality between saving and investment, the rate of interest will rise.

This is shown in the figure to rise from Oe to Or’. At this interest rate, the saving curve SS intersects the investment curve IT at E’. Consequently, both saving and investment equal the quantity shown as OB. Thus whatever is saved gets invested through interest rate flexibility.

The Quantity Theory of Money and Price Level:

The validity of Say’s Law in a money economy directly depends on the classical quantity theory of money which states that the general price level changes directly and proportionately to the supply of money. Algebraically stated the theory states that MV = PT where M, V, P and 7′ are the supply of money, velocity of money, price level and the volume of transactions. The equation tells that the total money supply MV equals the total value of output PT in the economy.

Assuming V (the velocity of money) and T (the total output) to be constant, a change in the supply of money (AY) causes a proportional change in the price level (P). This is based on the assumption that money acts only as a medium of exchange.

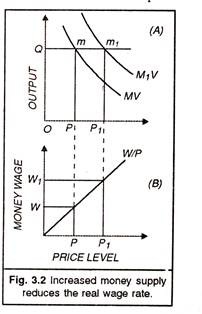
Let us show the main idea behind the quantity theory of money and its working in a competitive economy. The relation between quantity of money, total output and price level is shown in Figure 3.2 (A) where the price level is taken on the horizontal axis and the total output on the vertical axis. MV is the money supply curve which is a rectangular hyperbola.

This is because the equation MV = PT holds on all points of this curve. Given the output level OQ, there would be only one price level (OP) consistent with the quantity of money as shown by point m on the MV curve. If the quantity of money increases, the MV curve will shift to the right: let it be shown as M_t K curve. As a result, the price-level would rise from OP to OP given the same level of output OQ.

Assuming that the velocity of money V remains the same, this rise in the price level is exactly proportional to the rise in the quantity of money, i.e., PP₁ = mm₁. Classicals believed that workers respond to the changes in real wage rate in deciding to offer more less labour and it is possible to determine the money wage consistent with a given real wage. This is explained in Figure 3.2 (B), where WIP is the real wage line or wage-price line. When the price level is OP. the money wage is OW. When the price level rises to OP the money wage also rises to OW₁ The wage-price combination OW₁= OP₁ is consistent with the full employment real wage level W/P of Figure 3.3 (A) which we have drawn below. The proportionality between money wages and real wages is ensured by the operation of the quantity theory.

Wages Flexibility and Employment:

During the days of the Great Depression, Professor A C. Pigou supplied the most logical part of the classical theory of employment. According, to Pigou, under free competition the tendency of the economic system is to automatically provide full employment in the labour market. Unemployment results from rigidity in the wage structure and state interference in the working of the free market economy.

When the state intervenes by recognising trade unions, passing minimum wage laws, etc., and labour adopts monopolistic behaviour, wages are pushed upto unreasonable levels and unemployment results. Prof. Pigou’s contention was that if all government interferences are removed and forces of competition are allowed to work freely, the market induced changes of wage rates will lead to full employment. As pointed out by Pigou, “With perfectly free competition……. there will always be at work a strong tendency for wage rates to be so related to demand that everybody is employed.” Professor Pigou illustrated his point by using the following equation:

N = q.Y/W

In this equation, N is the number of workers employed, q is the fraction of income earned as wages and salaries, Y is the full employment national income and W is the average money wage rate. If Y is a given, N can be increased only by a reduction in W. Thus, the key to full employment is a reduction in the real wage. To explain his point, Pigou employed a mixture of micro and macro-economics.

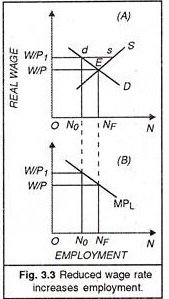
This is explained in the adjoining Figure 3.3. In panel (A), Sis the supply curve of labour and D is the demand curve for labour. If the intersection of the two curves at E shows the point of full employment N_f then it is the real wage IV/P at which full employment is secured. If the real wage is maintained at a higher level such as W/P₁ supply exceeds the demand for labour by sd and we find that N₀N_f labour is unemployed.

It is only when the wage is reduced to the level W/P that the unemployment disappears and the level of full employment is attained. This is shown in panel (B) of the figure where MP₁ is the marginal product of labour curve which slopes downward as more labour is employed. Since every worker is paid wages equal to his marginal product, the full employment level AY is reached when the wage rate falls from W/P₁ to W/P level.

Now the essence of the classical model is clear. In the classical model of employment, changes in money wages and real wages are directly related and are proportional. This follows from adoption of the classical quantity theory of money and prices.

When there is a cut in the money wage, the real wage is also reduced to the same extent which reduces unemployment and ultimately brings full employment in the economy. This relationship is based on the assumption that prices are proportional to the quantity of money.

It is argued that in a competitive economy a reduction in the money wage reduces the cost of production and prices of products thereby raising their demand. In order to meet the increased demand for the different products, more workers are employed to produce them.

The Classical Production Function:

Having analysed the working of the money, capital and labour markets, we are in a position to describe the classical production function for the economy as a whole. The classical argument runs thus: As employment increases, total output also increases till full employment is readied. But when the economy is at the full employment level, total output becomes stable. Thus given the stock of capital, technological knowledge and resources, a price is relation exists between total output and the amount of employment.

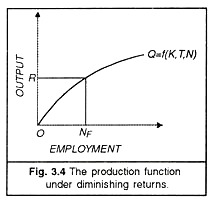
Total output is an increasing function of the number of workers. The economy’s short run production function is shown in Figure 3.4 as or curve which is labeled as Q =f (K, T, N), that is, total output 0 is a function of the capital stock K. of technological knowledge T, and the number of workers, N.

This production function shows that in the short run the total output is an increasing function of the number of workers, given the capital stock and technological knowledge. We find that the total output curve continues to rise but the rate of rise in total output diminishes as more workers are employed. This implies ‘diminishing returns’ to the use of labour and capital resources in the short run. In the Figure, the total output OR corresponds to the full employment level N_f as it is derived from Fig. 3.3 (B).

The classicists believed that under normal competitive conditions full employment will be maintained without causing inflation. Perfect competition among employers to hire more workers will not bid wages above the full employment level, and there will be no possibility of cost inflation in the highly competitive economy. Further, due to the operation of Say’s law, the full employment level of output will create aggregate demand equal to that potential output level.

It is the increase in aggregate demand beyond potential output which causes inflation. But the mechanism of the rate of interest prevents aggregate demand from increasing beyond the potential output. We know that inflation is caused by an increase in the quantity of money being more than what can be absorbed by the expanding output.

The competitive economy prevents this in the classical theoretical framework because an increase in the quantity of money increases only the absolute price level and not relative prices. Hence the assumption of full employment without inflation in the classical system can be considered valid for the long period. Depression and inflation are only temporary occurrences.

Complete Classical Model Summarised:

In its simplest form, the classical theory of unemployment is an analysis of output and employment in the interrelated labour, money and goods markets. We can precisely write the classical macro model through the following set of equations:

(1) Q=………………… F (K, T, N) (Production function)

(2) N_s=f₁ (W/P)………. Labour – Supply function

(3) N_d = f₂ (W/P)……… Labour – demand function

(4) S=f₃ (r)……….. Saving is a function of the rate of interest (r)

(5) I =f₄ (r)…………. Investment function

(6) S = I………… Equilibrium of the capital market

(7) MV= PT…………. The general price-level function (Quantity Theory)

(8) N_s = N_d……. The labour market equilibrium.

We take up the relevance of these equations to the figures drawn earlier. In the labour market, the demand for labour and the supply of labour determine the level of employment in the economy. Both are functions of the real wage rate (W/P). It is the point of intersection of the demand and supply curves of labour which determines the equilibrium wage rate and the level of full employment. They are W/P and N_f respectively in Figure 3.3.

The total output, in turn, depends upon the level of employment, given the capital stock and technological knowledge. The relation is shown by the production function Q =f (K, T,N) which relates total output OQ to N_f level of full employment in Fig. 2.4 which exactly equals N_f in Figure 3.3. Further, it is the mechanism of the rate of interest which brings about the equality of saving and investment so that the amount of commodities demanded should remain equal to the amount supplied at the full employment level, as shown in Figure 3.1.

Equilibrium in the money market is represented by the equation MV = PT. It explains the price level corresponding to the full employment level of output. It is OP₁ corresponding to OQ level of output in Figure 3.2 (A). Thus it can be said, that the classical model was perfectly logical, given its assumptions. The policy implication of the classical model was that the state should follow a non-intervention policy in economic affairs.