The Revealed Preference Hypothesis (With Diagram)

Samuelson introduced the term ‘revealed preference into economics in 1938. Since then the literature in this field has proliferated.

The revealed preference hypothesis is considered as a major breakthrough in the theory of demand, because it has made possible the establishment of the ‘law of demand’ directly (on the basis of the revealed preference axiom) without the use of indifference curves and all their restrictive assumptions.

Regarding the ordering of consumers’ preferences, the revealed preference hypothesis has the advantage over the Hicks- Allen approach of establishing the existence and the convexity of the indifference curves (it does not accept them axiomatically). However, the indifference curves are redundant in the derivation of the demand curve. We will first examine the derivation of the ‘law of demand’; we will then show how indifference curves can be established.

Assumptions:

1. Rationality:

The consumer is assumed to behave rationally, in that he prefers bundles of goods that include more quantities of the commodities.

2. Consistency:

The consumer behaves consistently, that is, if he chooses bundle A in a situation in which bundle B was also available to him he will not choose B in any other situation in which A is also available. Symbolically

if A > B, then B !> A

3. Transitivity:

If in any particular situation A > B and B > C, then A > C.

4. The revealed preference axiom:

The consumer, by choosing a collection of goods in any one budget situation, reveals his preference for that particular collection. The chosen bundle is revealed to be preferred among all other alternative bundles available under the budget constraint. The chosen ‘basket of goods’ maximizes the utility of the con­sumer. The revealed preference for a particular collection of goods implies (axiomatically) the maximization of the utility of the consumer.

Derivation of the demand curve:

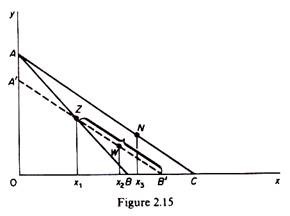
Assume that the consumer has the budget line AB in figure 2.15 and chooses the collection of goods denoted by point Z, thus revealing his preference for this batch. Suppose that the price of x falls so that the new budget line facing the consumer is AC. We will show that the new batch will include a larger quantity of x.

Firstly, we make a ‘compensating variation’ of the income, which consists in the reduction of income so that the consumer has just enough income to enable him to continue purchasing Z if he so wishes. The compensating variation is shown in figure 2.15 by a parallel shift of the new budget line so that the ‘compensated’ budget line A’B’ passes through Z. Since the collection Z is still available to him, the consumer will not choose any bundle to the left of Z on the segment A’Z, because his choice would be inconsistent, given that in the original situation all the batches on A’Z were revealed inferior to Z.

Hence the consumer will either continue to buy Z (in which case the substitution effect is zero) or he will choose a batch on the segment ZB’, such as W, which includes a larger quantity of x (namely x₂). Secondly, if we remove the (fictitious) reduction in income and allow the consumer to move on the new budget line AC, he will choose a batch (such as N) to the right of W (if the commodity x is normal with a positive income effect). The new revealed equilibrium position (N) includes a larger quantity of x (i.e. x₃) resulting from the fall in its price. Thus the revealed preference axiom and the implied consistency of choice open a direct way to the derivation of the demand curve: as price falls, more of x is purchased.

Derivation of the indifference curves:

Although not needed for establishing the law of demand, indifference curves can be derived and their convexity proved by the revealed preference hypothesis. The indifference-curves approach requires less information than the neoclassical cardinal utility theory. But still it requires a lot from the consumer, since the theory expects him to be able to rank rationally and consistently all possible collections of commodities.

Samuelson’s revealed preference theory does not require the consumer to rank his preferences or to give any other information about his tastes. The revealed preference permits us to construct the indifference map of the consumer just by observing his behaviour (his choice) at various market prices, provided that:

(a) His choice is consistent,

(b) His tastes are independent of his choices over time and do not change,

(c) That the consumer is rational in the Pareto sense, that is, he prefers more goods to less.

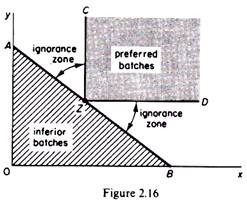
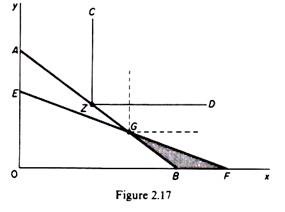
Assume that the initial budget line of the consumer is AB in figure 2.16 and he chooses the batch Z. All the other points on the budget line and below it denote inferior batches to Z. If we draw perpendiculars through Z, CZ and ZD, all the batches on these lines, and in the area defined by them to the right of Z, are preferred to Z because they contain more quantity of at least one commodity. Batches of goods in the remaining area (below CZD and above the budget line) are still not ordered. However, we may rank them relative to Z by adopting the following procedure. Let the price of x fall so that the new budget line EF passes below Z (figure 2.17).

The consumer will choose either G or a point to the right of G (on GF), since points on EG would imply inconsistent choice, being below the original budget line and hence inferior to G. Assume that the consumer chooses G. Using the transitivity assumption we have

Z > G (in the original situation)

G > (GBF) (in the new budget situation)

hence Z > (GBF)

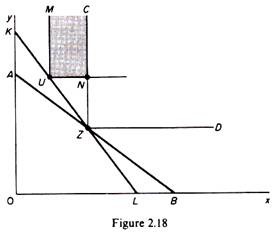
In this way we managed to rank all the batches in GBF relative to Z. We may repeat this procedure by drawing budget lines below Z and defining gradually all the batches of the ‘lower ignorance zone’ that are inferior to Z. Similarly we may rank (relative to Z) all the batches of the ‘upper ignorance zone.’ For example, assume that the price of x increases and the new budget line KL passes through Z. The consumer will either stay at Z or choose a point such as U on KL (figure 2.18).

Using the rationality assumption we find

(M UN) > U

From the revealed preference principle

U > Z

and from the transitivity postulate

(MUN) > Z

Thus we managed to rank the batches in (MUN) as preferred to Z. Repeating this procedure we may gradually narrow down the ‘ignorance zone’ until we locate the in­difference curve within as narrow a range as we wish. Hence the revealed preference axiom permits us to derive the indifference curve from the behaviour (actual choice) of the consumer in various market situations.

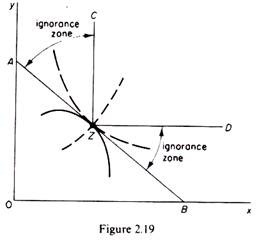
The convexity of the indifference curve may be established graphically as follows. Let us redraw the original budget situation (figure 2.19). We observe that the indifference curve through Z must be somewhere in the ignorance zone and must be convex, because it cannot have any other shape. The indifference curve cannot be the straight line AB because the choice of Z shows that all the other points on AB are inferior to Z (hence the consumer cannot be at the same time indifferent between them).

It cannot be a curve or line cutting AB at Z, because the points below Z would imply indifference of the con­sumer, while he has already revealed his preference for Z. Finally, the indifference curve cannot be concave through Z, because all its points have already been ranked as inferior to Z (they contain less goods). Hence the only possible shape of the indifference curve is to be convex to the origin.

Critique of the revealed preference hypothesis:

We have already said that Samuelson’s revealed preference theory is a major advance­ment to the theory of demand. It provides a direct way to the derivation of the demand curve, which does not require the use of the concept of utility. The theory can prove the existence and convexity of the indifference curves under weaker assumptions than the earlier theories. It has also provided the basis for the construction of index numbers of the cost of living and their use for judging changes in consumer welfare in situations where prices change.