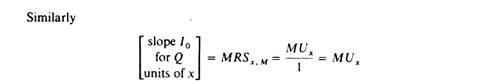The Consumers’ Surplus (With Diagram)

Read this article to learn about Consumers’ Surplus – explained with diagram!

The Marshallian Surplus:

The consumers’ surplus is a concept introduced by Marshall, who maintained that it can be measured in monetary units, and is equal to the difference between the amount of money that a consumer actually pays to buy a certain quantity of a commodity x, and the amount that he would be willing to pay for this quantity rather than do without it.

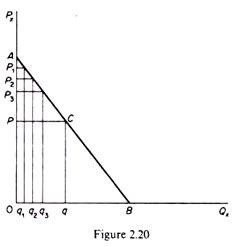
Graphically the consumers’ surplus may be found by his demand curve for commodity x and the current market price, which (it is assumed) he cannot affect by his purchases of this commodity. Assume that the consumer’s demand for x is a straight line (AB in figure 2.20) and the market price is P. At this price the consumer buys q units of x and pays an amount (q) . (P) for it.

However, he would be willing to pay P₁ for q₁, P₂ for q₂, P₃ for q₃ and so on. The fact that the price in the market is lower than the price he would be willing to pay for the initial units of x implies that his actual expenditure is less than he would be willing to spend to acquire the quantity q. This difference is the consumer’s surplus, and is the area of the triangle PAC in figure 2.20.

The Marshallian consumers’ surplus can also be measured by using indifference- curves analysis.

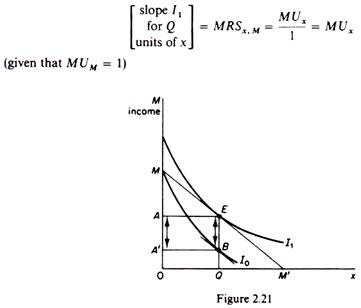
In figure 2.21 the good measured on the horizontal axis is x, while on the vertical axis we measure the consumer’s money income. The budget line of the consumer is MM’ and its slope is equal to the price of commodity x (since the price of one unit of monetary income is 1). Given P_x, the consumer is in equilibrium at E. he buys 0Q quantity of x and pays AM of his income for it, being left with 0A amount of money to spend on all other commodities.

We next must find the amount of money which the consumer would be willing to pay for the 0Q quantity of x rather than do without it. This is attained by drawing an indifference curve passing through M. Under the Marshallian assumption that the MU of money income is constant, this indifference curve (and any other of the indifference map) will be vertically parallel to the indifference curve I₁; the indifference curves will have the same slope at any given quantity of x. For example, at Q the slope of I₁ is the same as the slope of I₀

Given that the quantity of x is the same at E and B, the two slopes are equal.

The indifference curve I₀ shows that the consumer would be willing to pay A’M for the quantity 0Q, since point B shows indifference of the consumer between having 0Q of x and 0A’ of income to spend on other goods, or having none of x and spending all his income M on other goods. In other words A’M is the amount of money that the consumer would be willing to pay for 0Q rather than do without it.

The difference

A’M – AM = AA’ = EB

is the difference between what the consumer actually pays (AM, given P_x) and what he would be willing to pay for 0Q of x. That is, this difference is the Marshallian consumers’ surplus.

An alternative measure of the consumer’s surplus:

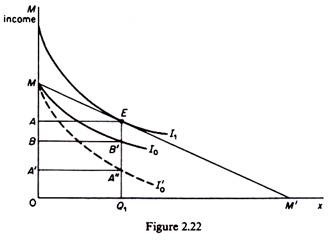
In the above analysis it was assumed that the marginal utility of money is constant. Clearly this assumption is very strong. If we relax this assumption, the size of the consumer’s surplus is smaller than the Marshallian theory of cardinal utility implies. To see this, in figure 2.22 we start from an initial equilibrium E, defined by the tangency of the budget line MM’ to the highest possible indifference curve I₁. Here the consumer buys 0Q₁ of x at the market price P₁, which is the slope of indifference curve I₁ at point E, since at this point given P_M = 1.

MRS_{x, M} = P_x / P_M = P_x

The actual expenditure of the consumer for 0Q₁ is P.Q₁ = AM.

To find the maximum amount of money the consumer would be willing to pay for the same quantity (0Q₁) rather than do without, we draw an indifference curve I₀ through M, in figure 2.22. This indifference curve is flatter than I₁ for any given quantity of x, showing that the marginal utility of money changes inversely with the amount of money income.

Thus the consumer would be willing to pay BM for Q₁ rather than do without, and the consumers’ surplus is the difference

BM — AM = BA — BE

To compare this measurement of the consumer’s surplus with the Marshallian measure we draw through M the indifference curve I’₀ vertically parallel to I₁ implying con­stant MU of money. Under this assumption the (Marshallian) consumer surplus is EA” which is clearly larger than EB’, the surplus under the assumption of decreasing MU of money income.

Note:

Both at E and B’ the quantity of x is the same (0Q₁), so that the MU_X is constant at these two points. However, the income left to be spent on other goods (0A) is larger at E as compared with B’ (where the remainder income is 0B). Hence at B’ the MU of money income is higher than at E. Thus, comparing the slopes of I₁, at E and of I₀ at B’ we see that

that is, the slope of I₀ is smaller than I₁, for any given quantity of x.