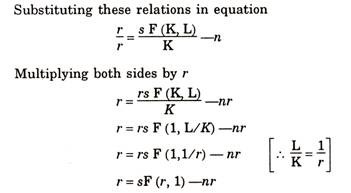Solow’s and Meade’s Contribution towards Economic Growth

Let us make an in-depth study of the Solow’s and Meade’s contribution towards economic growth.

Solow’s Contribution towards Economic Growth:

Among the neo-classical writers, the contribution of R.M. Solow is very remarkable since it emphasised that the economic system, over a long time, will not traverse a Knife-edge equilibrium growth path, as had been discussed by Harrod, Domar and Hicks.

Solow gives the following basic equation:

K = sF (K, L₀ e^nt)……..(viii)

Here K is the rate of increase of capital stock, s is the fraction of output that is saved. F (K, L₀ e^nt) is the production function which specifies that output is the function of capital (K) and labour (L).

The labour force in any time period is determined as:

L(f) = L₀e^nt

Here t is time and n is the rate at which labour grows. Solow considers n as equivalent to Harrod’s natural rate of growth in the absence of technological progress.

The (viii) equation specifies the rate of accumulation of capital stock which is consistent with the growth of labour force.

To demonstrate that there is always a capital accumulation path consistent with any rate of growth of labour force, R.M.

Solow introduces the following equation:

r = s F (r, 1) — nr … (ix)

In equation (ix), r is the ratio of capital to labour (K/L), r is the rate of increase of capital-labour ratio per unit of time.

The equation (ix) can be derived as follows:

r/r = K/K – L/L ……..(x)

Here the relative rate of change of r is equal to the difference between the relative rates of K and L.

Now L/L = n and K = sF(K, L)

Diagram Representation:

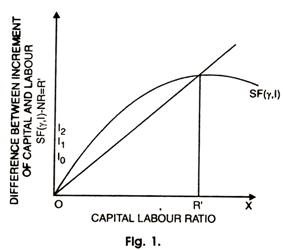
On the basis of this fundamental equation, Solow analysed the possible growth patterns with the help of diagram:

The line passing through origin in Fig. 1 with slope n represents function nr. The other curve represents the function sF (r, 1). It is so drawn as to show the decreasing marginal productivity of capital. At the point of intersection of two curves nr = sF(r, I) and r=0. In Fig. 1, this intersection determines r capital- labour ratio. In case this ratio is established, it will be maintained and capita and labour will grow thence-forward in proportion. By constant returns to scale, real output will also grow at the same relative rate n, and output per head of labour force will also be constant.

If r>r, then nr > sF (r, 1) and r will tend to fall so as to approach r. On the contrary, if r<r, then nr < sF (r, 1) and r will tend to increase upto r. This shows that the equilibrium value r is stable.

This provides the basis for Solow’s repudiation of Knife-edge equilibrium. In his words, “When production takes place under the usual neo-classical conditions of variable proportions and constant returns to scale, no simple opposition between natural and warranted rates of growth is possible. There may not be…… any knife edge. The system can adjust to any given rate of growth of the labour force, and eventually approach a state of steady proportional expansion.”

Output Growth with Technical Progress:

In the preceding discussion, the index of technological know-how was assumed as constant. It is quite obvious that technological progress is a force which is capable of raising the rate of growth above what it would have been otherwise. Denoting the rate of technological progress by 8 T/T, the rate of growth of output is

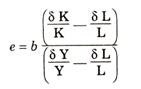
The proportion of growth rate of output per worker due to the technological advance is determined by the difference between the proportion e and 1.

Meade’s Contribution:

Prof. Meade examines the determinants of economic growth in a single product economy in which there is perfect substitutability in production between capital goods and consumption goods.

In such an economy, the net output produced depends upon following four factors:

(i) The amount of existing stock of machines;

(ii) The amount of labour available for productive employment;

(iii) The amount of land or natural resources available for productive use in the economy, and;

(iv) The state of technological knowledge which can be assumed to be improving constantly. Thus production is a function of the stock of capital, amount of labour, amount of land and level of technique. This can be expressed as,

Y = f(K, L, N, t)

where Y = net output, K = the existing stock of machines, L = the amount of labour, N = the amount of land, and t = time over which technological progress takes place.

Three cases:

Now three things may happen to increase the volume of Y:

(i) The stock of machines (K) may increase because the community is saving a part of its income and is thereby accumulating real capital. The increase in capital stock may be represented by ∆K. It will increase the output by V∆K if V is the marginal net physical product of a machine.

(ii) The working population (L) may grow. If it-grows by ∆L then the output will increase by WAL where W represents the marginal product of labour.

(iii) With the passage of time Y would rise even if K, L and N remain constant. This increase is due to technical progress and it may be represented by ∆Y’.

If land or natural resources remain constant, the increase in income will be the total of the increase in output due to these influences.

It can be put up as follows:

∆Y/Y = V∆K/Y + W∆L/ Y + ∆Y’/Y

Developed economies and hence their ideas and policies have little relevance for under-developed countries. For example, their policy of free trade and international specialisation can hardly solve the problems of under-developed countries.