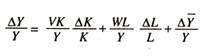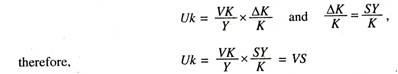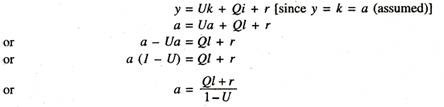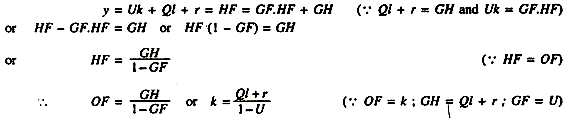Meade’s Mode (Discussed with Diagram)

Read this article Meade’s model in neo-classical theory of economy growth.

Introduction:

Prof. Meade in his book “A Neo-Classical Theory of Economic Growth” has developed a neo-classical model of economic growth by including population and manpower supply as an important determinant of growth of an economy.

He examines the conditions of steady growth, where population is growing at a constant proportionate rate while technical progress is constant. In this way, he tries to establish a relation between population growth and income growth.

According to him, an economy grows for three reasons—because net savings are being made out of current income so that the stock of capital is growing; because the working population is growing; and because technical progress allows more and more output to be produced by a given amount of resources.

The main assumptions of Meade’s model are as follows:

Assumptions:

(a) There is a closed economy with no-economic or financial relations with other countries;

(b) There are constant returns to scales;

(c) Economic activities are performed in free and perfect competition;

(d) There is no state interference involving taxes or expenditure;

(e) Consumption goods and capital goods are the only two commodities produced in the economy;

(f) Machines constitute the only form of capital;

(g) There is perfect substitutability between capital goods and consumption goods in the production process;

(h) He assumes that each year a certain percentage of machinery depreciates and needs replacement;

(i) The ratio of labour to capital can be varied with ease both in the short and long-run.

Conditions of Growth:

According to him net output produced by an economy depends on four factors—net stock of capital in the form of instruments of production, the labour force, land and natural resources and technical knowledge.

These factors are expressed in the basic production function as:

Y = F (K, L, N, t)

where Y is net national income, K is the existing stock of machines, L the amount of labour, N the amount of land and natural resources and t the technological progress that take place over time. Y may increase because the stock of machines (K) may increase on account of increased saving, thereby leading to accumulation of real capital.

The increase in capital stock is represented by AK and will increase the income or output by V . ∆K, where V is the marginal net physical product of a machine, Again, Y may increase because working population (L) may be growing. If it grows by ∆L, then the income or output will increase by W. ∆L, where W represents the marginal physical product of labour.

Further, Y or O may increase in technical progress over time, even if K, L and Nremain constant. The increase in Y or O due to technical progress is shown by Ay. Thus, if N remains constant (natural resources are assumed to be fixed), the increase in income (Y) will be the sum total of the contributions made by L, K, t, which are increasing that is:

∆Y = V. ∆ K + W ∆L + ∆Y

In other words the increase over the year in the rate of annual net output (∆K) is equal to the increase in the stock of machinery (∆K) multiplied by its marginal product (V) plus the increase in the amount of labour (∆L) multiplied by its marginal product (w) plus the increase in the rate of annual output due simply to technical progress (∆Y )

The proportionate rate of growth of output or the ratio of increase to initial amount, therefore is:

where ∆Y/Y is the annual proportionate rate of growth of income or output; ∆K/K annual proportionate rate of growth of the stock of machines or capital; annual proportionate rate of growth of working labour force; and ∆Y/Y annual proportionate rate of growth of income due to technical progress.

Let these four proportionate rates of growth by expressed as y, k, I and r respectively, VK/K (MPP of capital) represents the proportion of (Y) as net national income going to the owners of capital as net profit and is expressed as U. Similarly, WL/L (MPP of labour) represents the proportion of Y going to wages and is expressed as Q.

The above basic production function and relationships can be expressed as:

y = Uk + Ql + r

This equation shows that the growth of an economy (y) is a weighted sum of three other outputs (growth rates)—the sum of the growth rate of capital (k) weighted by the proportion of national income going as profits (U); the growth rate of labour (I) weighted by the proportion of national income going as wages (Q); plus the growth rate of technical progress (r). In other words, the rise in per capita real income (y – I) shows the growth of an economy. If y increases by 10 per cent per annum and I increases by 8 per cent per annum, income per head will increase by about 2 per cent per annum.

The growth rate of real income per head will therefore be:

y – I = Uk- (1 – Q)l + r.

In the above equation y – I is the difference between the growth rate of total income and the growth rate of working labour force—which snows us the growth of real income per head. The equation also tells us that the rate of growth of income per head (y – I) will be increased by a rise in real capital weighted by its MPP (Uk) and also by technical progress (r)—but it is decreased or depressed by the growth rate of labour weighted by one minus the proportional marginal physical product of labour, i.e., (I – Q) I.

The middle term [- (I – Q) I] on the right hand side of the equation which tends to depress the growth rate of real income per head shows the tendency for diminishing returns to labour as the supply of labour is increased in relation to any given amount of land or capital. In order to introduce savings (S) into the above equation, Uk can be written in another way also. Since it is assumed that all savings are invested, the addition to the stock of capital (∆K) will be equal to the savings out of the net national income (SY), that is ∆K = SY therefore, ∆K/K=SY/K where SY represents the annual savings.

We know that:

The above basic relationship can also be expressed as follows:

y – I = VS – (1 – Q) l + r.

Thus, if S is 10 per cent of Y and MPP of capital (V) is 5 per cent per annum, the contribution of capital growth to increase in income will be 1/10 x 5 = ½ per cent per annum.

Changes in the Rate of Economic Growth:

The basic equation: Y – I = VS – (1 – Q) I + r lays down the conditions of growth. After analyzing the main factors or conditions which determine growth rate of real income, Prof. Meade analyzed the conditions under which the growth rate of real income will tend to increase or decrease, in other words, he analyzed the factors responsible for changes in the rate of economic growth. Assuming growth rates of population and technology (I and r) as given and constant, the changes in income per head (y – I) will depend upon the changes in the values of V, S and Q over time.

If I and r are unchanged but S goes up, capital per head will increase (due to increased savings), and the marginal product of capital (V) will fall (due to increase in the quantum of capital). Thus, VS in our basic relationship will be falling. Meade says that this fall may be neutralized or slowed down, if we keep in mind the possibility of substitution of capital for other factors.

Also, if we allow for improvement and progress in technology or change in r, the decline in the MPP of capital (V) will be offset. A rapid rate of technical progress (r) will tend to raise MPP of capital (V) over time. As a matter of fact, a rapid rate of technological progress can be expected to raise the marginal product of all the factors simultaneously—it all depends upon the nature of technical progress—whether it is labour using or labour saving. Machinery using technical progress will tend to raise U(VK/Y)

Thus, the nature of technical progress will affect the growth rate of real income per head and this, in turn, may lead to an increase in the volume of savings, thereby raising the VS as a whole. It is, therefore, clear that if population alone is assumed to be constant, the increase in income will depend on the productivity of capital (V), the amount of savings (S) and the state of technology (r), that is: y – VS + r. It may also be noted that in case technical progress (r) remains constant, economic growth (y) will entirely depend on VS.

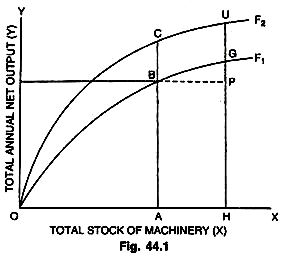
The higher the rate of technical progress (r) the higher the marginal product of capital V; the more machine using the nature of technical progress in the process of production in the beginning, the lower may be the initial proportion of income saved (S) due to heavy investment in machinery—but as income increases with it savings will rise and the more readily machinery is substituted for land and labour, S will rise over time because of rise in income per head and also because of a shift of income towards profits. The effect of technical progress (r) on growth rate of income is illustrated with the help of the given Fig. 44.1.

In the diagram, we measure stock of machinery (K) along horizontal axis and total net income (Y) is measured along vertical axis. The curve OF₁, shows the amount of output produced in the first year by a given amount of machinery and state of technical progress. If capital is OA in the first year, then the output will be AB. If the amount of capital is increased to OH, then GH is the amount of income or output produced. As the slope of the curve at G is less than at B, the marginal product of machinery will be lower.

In the second year, when the technical progress has taken place (there is a rise in r), a new curve OF₂ lying above OF₁, shows the various amounts of output that can be produced with different amounts of capital with higher level of technology. In the first year, we get AB output on account of OA capital but in the second year, the same amount of capital OA brings us higher output AC—which is entirely due to technical progress (r). Similarly, with OH amount of capital, it is now possible to produce a higher output HD.

Conditions of Steady Growth:

Prof. Meade is not only concerned with the determinants of growth and the changes in the rate of growth but he also examines the conditions of steady growth, under the circumstances when population is growing at a constant proportionate rate while the technical progress (r) remains constant. With a constant growth rate of population (I), the growth rate of income per head (y – I) will be constant if the growth rate of total output (y) remains constant. In other words, Meade examines those conditions which would ensure a constant growth rate of total output under these conditions.

These conditions are—that all elasticities of substitution between various factors of production are equal to unity; that technical progress is neutral towards all factors; and that the proportions of profits saved, wages saved and of rents saved are all constant. Let S_v, S_w and S_g represent the proportions of national income saved out of profits (U), saved out of wages (Q) and saved out of rents (Z). Therefore, total savings (S) will be the sum of the savings out of profits, wages and rents, that is:

S = S_VU + S_WQ + S_gZ

The growth fate of output is given by our basic equation:

y = Uk + Ql + r

In this equation, U, Q, I and r are assumed to be constant, therefore, y depends on k. It is only if k is constant that y will be constant. But k is the growth rate of capital stock which is equal to SK/K where SY represents the amount annually added to the capital stock (K) through savings. Since U, Q, Z, are constant, therefore, S_v, S_w and S_g are also constant and, therefore, their sum S as a ratio of Y will be constant. Since S is constant, therefore SY/K will be constant, only if, Y/K is constant Y/K will be constant if both Y and K grow at the same proportional rate per annum that is, if Y = K or y = k.

It can, therefore, be concluded that if the growth rate of capital stock is equal to the growth rate of income, then the rate of growth of income will be constant. Thus, the equilibrium position ultimately depends on the rate of accumulation of capital stock in the economy. According to Prof. Meade, there is a unique or critical growth rate of capital stock, which equalises the growth rate of income (y) and the growth rate of capital stock (k). A higher or lower growth rate in capital than this capital growth rate will not equalise y and k and the condition of steady growth will not be fulfilled. If we put a for the critical growth rate, then our basic equation can be written as follows:

This equation means that if the critical growth rate of capital stock (a) is equal to Ql+r/1-U then the growth rate of income (y) will also be QI+r/1-U and the condition necessary for steady growth is fulfilled. This is, of course, an equilibrium position. A deviation from it is indicated by the excess or deficiency of actual savings and capital accumulation above or below the rate which is equal to the income growth rate. It is illustrated by numerical examples:

If for some reason the rate of accumulation for capital stock SY/K is greater than the critical growth rate (Ql+r/1-U), that is, if SY/K > QI+r/1-U,then the income will grow at a lower than the capital stock, savings will decline and the growth rate of capital will also decline till it comes down and becomes equal to the critical growth rate Ql+ r/1-U. Conversely, if SY/KQI+r/1-U , the income will increase more rapidly than the capital stock and as a result savings will rise and so also the growth rate of capital SY/K till it rises and becomes equal to the critical growth rate (Ql+r/1-U).

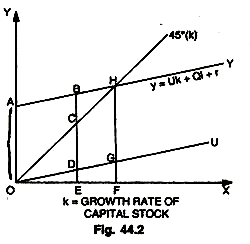
Thus, Meade’s neo-classical model draws attention to the role of population growth, capital increase and technology in determining the increase of income per head and also _Y to the conditions under which a stable growth of per capita income is possible when populations increasing along with other determinants. The Fig. 44.2 illustrates Meade’s model of steady economic growth. X axis measures the growth rate of the stock of capital; Y axis measures the growth rate of national income.

The U curve represents the proportional marginal product of capital (MPP of capital) ; the curve AY shows the total growth rate of national income (y = Uk + Ql + r) ; and the 45° line (k) shows the growth rate of the capital stock. Suppose, in the beginning the growth rate of capital stock is OE; the growth rate of national income (y) will be BE. But BE = BD + DE (BD due to population growth and technical progress = Ql + r, and DE due to MPP of capital or capital accumulation).

But at this stage BE (income, y) is greater than capital stock (k), that is, BE > CE. As a result, k will have to rise and will go on rising till point F on the X axis, where it meets Ay curve on point H, thereby bringing an equality of y and k (y – k, the 45° line). This shows the final condition and stage of steady economic growth, at which the rate of growth of capital (k or HF or OF) is equal to the rate of growth of income (y or HF).

Thus, the economy is growing at that unique or critical rate of growth (a) at which the rate of growth of income is equal to the rate of growth of capital stock (HF — OF).

It can be shown as follows:

 

Critical Evaluation:

Meade’s model, no doubt, marks an improvement over the H-D models insofar as it takes into account the supply side of capital, labour resources, role of technology and population growth in the process of economic development. But it has great limitations of unrealistic assumptions leading to abstract theoretical structures: The incorporation of many classical assumptions in Meade’s model like perfect competition, perfect mobility, constant returns to scale, perfect substitutability of factors of production make the model too abstract to be applicable to the situations of real world.

It is too mathematical a model, which contains a number of equations based on complex inter-relations of various variables. For example, Meade’s assumptions of constant rate of growth of population, the elasticities of substitution of three factors equal to unity, constant technical progress and neutral towards all factors, constant proportionate of wages, rents and profits saved, under which y = k are all too abstract and unrealistic in nature. Meade’s model assumes closed and laissez-faire economy and neglects the role of social, political, religious, cultural factors, which play an important role in economic growth.

According to Prof. Butterick, there is no place of uncertainty or lags in Meade’s model. The inter-relations and changes thereof in all variables in Meade’s model have been regarded as certain and follow automatically. Meade merely postulates that monetary policy is such as will keep the prices of consumption goods constant, while money wage rates are such as to ensure full employment.

He dodges the problem of foresight by making capital goods perfectly versatile or malleable. It means that the ratio of labour to capital or machines can be changed both in the short and long-run. All these elements go to make Meade’s model less practical and less applicable, especially, in underdeveloped and developing economies.

Economic development is a very complex phenomena and it is not possible to grasp the true nature of the process of growth unless we duly understand and bring into picture the significance of the non-economic factors. Meade’s growth model concentrates too much on the factors that help accumulation of capital and its influence on the rate of growth of income; but capital accumulation, itself is more an effect, almost a symptom of economic growth than its primary cause.