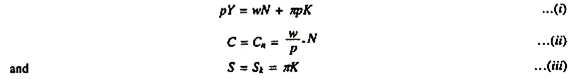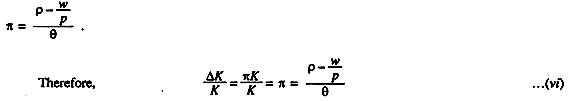Joan Robinson’s Model (Discussed with Diagrams)

Read this article to learn about the Joan Robinson’s model in neo-classical theory of economic growth.

Introduction:

Joan Robinson’s growth model clearly incorporates the problem of population growth in a developing economy and analyses the effects of population on the rate of capital accumulation and growth of output.

Mrs. Joan Robinson’s model of economic growth is based on two basic conditions, i.e:

(i) Capital formation depends upon the manner of distribution of income, and

(ii) The rate at which the labour is used depends upon the supply of capital and that of labour. Her model is given in her book ‘The Accumulation of Capital’ based on the capitalist rules of the game.

Assumptions:

She makes the following assumptions:

(a) Total income in real terms is divided between two classes—workers and entrepreneurs.

(b) Workers spend all their wages on consumption and save nothing.

(c) Profit seekers save and invest all their profits and consume nothing. If they have no profits, they cannot accumulate and if they don’t accumulate, they have no profits.

(d) That capital and labour are combined in fixed proportions to produce a given output (this assumption was dropped later on) i.e., there is no technological change. In other words, there is a given technique of production within fixed proportion of capital to labour.

(e) Her entire argument runs in ex-post terms. There is no change in the price level.

(f) There is a laissez-faire closed economy.

(g) There is no shortage of labour, the entrepreneur can find as much labour as they wish to enlarge the path of steady growth which in the Robinson framework is seen as a constant rate of capital accumulation, necessitates a rate of profit that leads businessmen to perpetu­ate the past rate of accumulation such a profit rate needs, for example, the condition that there be no surplus or scarcity of labour, that is, the labour force should grow at the same rate as capital.

Features:

Mrs. Robinson’s model is a dynamic two sector model in which she examines what happens in the quasi-long period. Her main thesis is that of the two classes in the basic model, workers consume everything they get; while businessmen reinvest whole of their profits, as a result a fundamental identity follows ; ex-post investment equals ex-post profits. However, there is a limit to entrepreneurs attempt to invest all their profits—this limit is set by the minimum level of real wages on which the workers insist.

Within that limit—inflation barrier—there are other barriers set by financial monetary factors, productive capacity, balance of payments, etc. At each step of the growth of the economy, these barriers are pushed up higher and higher and within these constraints growth depends upon the energy of the entrepreneurs.

The process of growth is eased and barriers are overcome if there is smooth flow of innovations. The ultimate stage is the ‘Golden Age’ and the potential growth ratio of the Golden Age economy is akin to Harrod’s natural rate of growth G_n. Thus, she is interested in explaining the fundamental nature of economic growth according to the ‘capitalist rules of the game’? For this purpose she builds a verbal model and K.K. Kurihara built up a real model, which is given hereafter.

The distribution equation which is most significant in her growth model is shown as under.

Here C_n is workers consumption out of wage income (w/p.N) and SK saving out of profit income (K). In equation (i) above net investment means an increase in real capital (AK), therefore, we have

I= ∆K    ……………………(iv)

Considering equations (iii) and (iv) above, we can rewrite S and I relation as:

∆K = πK             ……………….(v)

Because (S = I). Therefore = ∆K /K =π or ∆ K /K = πK/K but from equation (iii) above, we know

Thus, the rate of growth of capital given by equation (vi) is the rate which is attainable by entrepreneurs by following the capitalist rules of the game, according to J. Robinson. This equation shows that the rate of growth of capital is capable of increasing, if the net return of capital (P-w/P) rise in greater proportion than the capital-labour ratio. In Ricardian terms it means that capital accumulation is strengthened by a fall in the real wage rate. It appears that she has brought us back to Ricardo’s theory of economic development, though via Keynesian door.

Coming to Mrs. Robinson’s notion of ‘Golden Age’ i.e., equilibrium with full employment of labour and full utilization of capital. This is possible, if we assume (K/N) = θ = constant in conditions of full employment and full utilization; an increase in the amount of fully employed labour is given by ∆N = ∆K/θ ( K/N = θ).

From this relation we can have the rate of growth of fully employed labour:

which shows that fully employed labour grows at the same rate as the rate of growth of capital, and which implies that capital must grow as fast as labour population, when capital-labour ratio (θ) remains constant. In other words, it shows that the rate of change in labour force (∆N/N) is equal to the rate of change in capital stock (∆K/K). Thus, given the perfect supply of labour, with respect to output, this equation signifies a golden age equilibrium with full employment of both labour and capital.

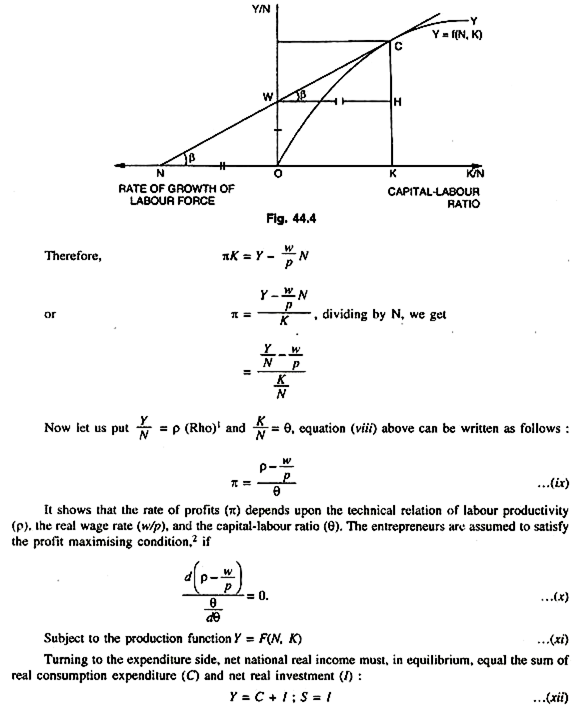
This is shown in Fig. 44.4, where Y is the net national income, N the amount of labour employed, K the amount of capital equipment utilized, p the average price of output as well as of capital equipment, w the money wage rate, and n the gross profits rate (including the interest rate) required for the normal utilization of the existing stock of real capital. Divide both sides of equation (i) above by p (the average price), we get the distribution equation in real terms:

Y = W/P N+ πK ,..(viii)

We want to find out the rate of profit shown as n in the equation so as to reach an equilibrium condition from demand side of the economy.

This is familiar Keynesian income-expenditure equation.

Let us convert it into forms consistent with Robinson’s assumptions, thus:

In this figure horizontal axis measures capital-labour ratio (K/N) in quadrant I. Vertical axis measures the labour income ratio or labour productivity (Y/N). OW is the minimum wage rate. In quadrant II, ON measures the rate of growth of labour force. OY shows the expansion path. A tangent is drawn touching at C. Now the rate of growth of capital = ∆I/I =Output- Input/ Input = Surplus/Input = HC/OW x OK =HC/WH x 1/OW (because tan β = tan β), therefore, HC /OK =HC/WH OK = WH = ON and OW = HC . Therefore, HC/WH 1/OW= OW/ ON x 1 /OW = 1/ON = the rate of growth of labour force. In other words, the rate of growth of surplus which is HC must be able to absorb the rate of growth of labour force which is ON here. This brings up to the ‘Golden Age’ according to Mrs. Joan Robinson.

Notion of Golden Age:

After analysing the role of capital accumulation on the growth of an economy, Mrs. Robinson proceeds to analyze the impact of population growth on economic development. An increase in population and labour supply without adequate increase in capital stock would result in a fall in the labour productivity and if the real wages remain constant, it will mean a fall in the rate of profit, which in turn, will adversely affect the rate of capital accumulation.

All this will result in increased unemployment as is usually the situation in underdeveloped countries. Full employment is possible only when the rate of growth of population is matched by the rate of growth in capital stock.

When this happens, that is, the growth rate of population and the growth rate of capital are equal, the economy is in fully employment equilibrium. This is Joan Robinson’s ‘Golden Age’. According to her when the technical progress is neutral and proceeding steadily, without any change in the time pattern of production, the competitive mechanism working freely, population growing (if at all) at a steady rate and accumulation going on fast enough to supply productive capital for all available labour, the rate of profit tends to be constant and the level of real wages to rise with output per man.

There are then no internal contradictions in the system; provided that political events cause no disturbances, and provided that entrepreneurs have faith in the future and desire to accumulate at the same proportional rate as they have been doing over the past, there is no impediment to prevent them from continuing to do so.

Total annual output and the stock of capital (valued in term of commodities) then grow together at a constant proportionate rate compounded at the rate of increase of the labour force and the rate of increase of output per man. We may describe these conditions a golden age (thus, including that it represents a mythical state of affairs not likely to obtain in any actual economy).

It is a stage of bliss, since consumption is increasing at the maximum technical feasible rate. In the words of Harrod the natural, the warranted and the actual rate of growth of national income are all equal whatever the rate of progress being maintained in Golden Age, it is always possible to progress further.

The limits to the rate of growth of wealth, over the long-run, is set not by technical boundaries but by the lethargy which develops when the load of competition and the rising wage ratio is blunted. The ‘golden age’ equilibrium with full employment of labour and full utilisation of capital can be maintained only if, the rate of growth of labour force (∆N/N) is equal to the rate of growth of capital stock (∆K/K). In other words, in equilibrium with full employment of labour and capital ∆N/N = ∆K/K. If, however, ∆N/N > ∆K/K there will be unemployment in the economy and vice-versa.

Thus, we find it is a useful concept introduced for purposes of rigorous theoretical analysis. It is not an ideal like full employment to be achieved through policy measures. It is an expository device. In fact, every rate of growth has an appropriate golden age and the main problem is how to find out that particular growth rate which is optimum for the economy under a set of conditions. Mrs. Robinson’s golden age is an era of plenty and not one of stagnation.

Thus, what matters most is the behaviour of profit-wage relation. In fact, this behaviour determines whether an economy can get on to the path of Golden Age equilibrium. According to her, it appears, capital accumulation according to the ‘capitalist rules of the game’ cannot expand unless the price of labour (real wage rate) is reduced relatively to the price of capital (roughly speaking the profit⁷ rate) and to the productivity of labour.

In a golden age economy the shares of wages and profits are constant and all elements in the economy expand in the same proportion, which shows that in such an economy there is neutral technical progress under an appropriate rate of capital accumulation. Again, in such an economy, there is perfectly definite rate of profit, ruling in the past, will continue in future and anybody, who is saving money, will be willing to lend it as a result, the rate of interest will not be much lower than the rate of profit. A constant capital-output ratio is visualised in ‘Golden Age’ and if this is so, it follows that shares of wages and profits will remain constant.

When ‘potential growth ratio’ is being realized, then, according to Mrs. Robinson the economy is in golden age. It is the highest rate of capital formation which can be permanently maintained at a constant rate of profit. The conditions of golden age require the growth ratio to be steady because frequent changes in the growth ratio disturb the tranquility of a golden age. This tranquility, however, may not be possible even when the growth ratio is stable. An increase in the total stock of capital is likely to slacken the urge to accumulate so that a stage of stagnation starts and the economy deviates from the path of golden age.

Evaluation:

Mrs. Robinson’s model has close kinship to Keynes’ aggregative approach because both happen to be macro-models. However, Keynes’ model is not truly dynamic. It is better to describe Keynes’ General Theory Aggregative Approach as short period macro-static model and to make it long period macro-dynamic model, the element of ‘growth’ has to be incorporated into it. If this is done the task of generalization of the General Theory may become complete.

Thus, we have explored Harrod’s world and Robinson’s golden age. But whereas Harrod-Domar make capital formation dependent on saving ratio (i.e. relating it to the aggregate income of the community and not to profit income alone) and capital productivity. Mrs. Joan Robinson makes capital accumulation dependent on the wage- profit relationship as well as on labour productivity, thus bringing her analysis quite close to a real market economy.

Again, it is not without significance to note that Joan Robinson approaches the question of capital accumulation from the standpoint mainly of labour while Harrod-Domar approach is from the view-point of capital. It is on account of these differences; it is said, that though Robinson’s model comes essentially to the same thing as those of Harrod and Domar yet they are different in approach, the latter being one factor model and the former being two factors model.

Thus, Joan Robinson’s chief contribution to post-Keynesian growth economies seems to be that she has integrated classical value and distribution theory and modern Keynesian saving-investment theory into one coherent system. However, this also seems to be the chief drawback, as far as policy application is concerned. For, unlike Harrod-Domar models, the Robinson model is not capable of being modified so as to introduce fiscal-monetary policy parameters—unless labour productivity, the wage rate, the profit rate, and the capital-labour ratio could be regarded as objects of practical policy— as they might be so regarded in a completely planned economy.

All the same, J. Robinson’s theory greatly deepens our understanding of the fundamental nature of capital accumulation according to the purely ‘capitalist rules of the game’. Finally, it must be observed that her growth model, while it is capable of yielding a stable equilibrium solution, nevertheless contains essentially as much instability as do the Harrod-Domar models of a lassez-faire economy.

Golden Age and Developing Economies:

Mrs. Robinson poses the question whether in her analysis or model the economy possesses any equilibrating mechanism, if and when it deviates from the ‘golden age’ path for some reason or the other. Suppose the economy deviates from the equilibrium path characterized by the inequality of ∆N/N >∆K/K that is, by labour population growing faster than capital accumulation, as in the case in most developing or under-developed countries. Whether or not the economy will again get back on the path of ‘golden age’ equilibrium depends in her view, on the behaviour of wage-profit relation.

The wage-profit relation may or may not behave in an equilibrating manner, depending on market conditions. Given the state of technology, the excess supply of labour would sooner or later reduce the wage rate and if prices are unchanged, real wage rate will stand reduced. This, in turn, will increase the profits and hence the rate of growth of capital so that it would catch up with the increase in population, so that once again ∆K/K = ∆N/N.

If, however, the real wage rate fails to fall due to any reason, the excess labour would fail to generate an equilibrating mechanism. Therefore, it is absolutely essential to enlarge the capital stock of an underdeveloped country by means of development planning. Similarly, converse is true of the case of capital accumulation growing faster than labour population, as in most advanced countries. However, the possibility of advanced economies returning to the path of golden age equilibrium is greater than that of underdeveloped economies.

The equilibrium is likely to be restored through technological improvement and the shifting of the whole production function so that the economy gets itself adjusted to a higher capital labour ratio. In advanced economies, even though the real wage rate were rigid, a change in labour productivity (ρ) or, in the capital ratio (θ) might well be such as to increase the profit rate and hence the rate of growth of capital in an equilibrating way as required in golden age path. This is where Mrs. Robinson goes beyond her basic model and becomes more Schumpeterian than Ricardian.

Furthermore, Mrs. Robinson’s model shows that such an important problem as economic growth should not be left to the capitalist rules of the game, especially in underdeveloped or developing economies. Her model shows even more convincingly than the H-D models that how dangerous and insecure it is to depend upon private profit seekers for the task of attaining stable economic growth of the economy, which is consistent with the needs of growing population and advancing technology.

Mrs. Robinson hints indirectly that poor economies need not follow the capitalist rules of the game for economic growth but should adopt Keynesian set up of mixed economy with fiscal and monetary policies geared to the task of encouraging autonomous investment.