Extension of the Solow Model (With Diagram)

Let us make an in-depth study of the Extension of the Solow Model. The two Extension of the Solow Model are: 1. Population Growth 2. Technological Progress.

Population Growth:

We now assume that population does not remain fixed. Instead, the population and the size of labour force grow at a constant rate n.

The Steady State with Population Growth:

We may now discuss how population growth, along with investment and depreciation, influences the accumulation of capital per worker. In the basic Solow model, while investment increases capital stock, depreciation reduces it. In this extended model, another factor changes the amount of capital per worker: the growth in the number of workers causes capital per worker to fall.

We assume that the number of workers is growing over time at the rate ‘n’ per period. So the change in capital stock per worker is

Δk = i – (δ + n)k … (20)

Equation (20) shows that new investment (i) increases k, while depreciation (δ k) and population growth (n) decrease k. These factors thus, together, determine capital stock per worker.

The term (δ + n)k may be treated as the break-even level of investment Which is necessary to keep per capita capital stock constant. Break-even investment has two components: replacement investment 8k which is a measure of depreciation of existing capital and new investment — the amount of investment necessary to provide new workers with capital.

The required amount of investment is nk because there are n workers for each existing worker arid k is the amount of capital per worker. Equation (20) shows that population growth, like depreciation, has a negative effect on the accumulation of capital per worker.

While depreciation reduces k by wearing out the existing stock of capital, population growth reduces k by dividing the existing stock of capital among more and more workers. So capital per worker falls.

With population growth we substitute sf(k) for i. The equation can then be expressed as

Δk = sf(k) – (δ + n)k … (21)

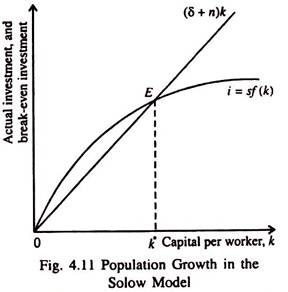
Fig. 4.11 shows what determines the steady-state level of capital per worker. We know that an economy is in steady state if capital per worker k remains constant at k*.

In the steady state the favourable effect of investment on the capital stock per worker just balances the negative effect of depreciation and population growth. This means that at the steady-state level of capital stock k*, Δk = 0, and i* = δk* + nk*.

As soon as an economy reaches the steady state, investment serves two purposes. A portion (δk*) replaces the depreciated capital and the balance nk* supplies the workers with the steady state amount of capital.

These Effects of Population Growth:

Population growth modifies the basic structure of the Solow growth in three ways:

1. Achieving Steady State:

Prima facie, population growth enables us to explain sustained economic growth. In the presence of population growth, capital per worker and output per worker remain constant in the steady state situation. Since the number of workers is increasing at the rate n, total capital and total output must also grow at the same rate if a steady state situation is to be maintained.

Thus, population growth can ex­plain sustained growth in GDP. However, since GDP per worker remains constant in the steady state, population growth cannot explain im­provement in the standard of living.

2. Explaining income differences among countries:

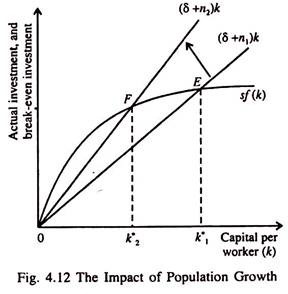
Population growth explains why some countries grow rich and others remain poor. Fig. 4.12 shows that an increase in the rate of population growth from n, to n₂ reduces the steady-state level of capital per worker from k* to k*₂. Since k* is lower, and because (y*) =f(k*), the level of output per worker y* is correspondingly lower.

Thus, if the rate of population growth increases from n, to n₂ the new steady state has lower level of capital per worker (k*₂) compared to that in the initial steady state (k*). The Solow model is thus able to predict that countries with high rate of population growth will have lower level of capital per worker and, thus, lower level of GDP per capita.

This is an observed reality. So the Solow model can explain the observed income differences among different nations of the world over time.

3. Altering the criterion for determining the Golden Rule level of capital:

Finally, population growth alters the criterion for determining the Golden Rule (consump­tion maximising) level of capital. Since consumption per worker c = y – i, steady-state output isJ{k*) and steady-state investment is (δ + n)k*, steady-state consumption can be expressed as

c* = f(k*) – (δ + n)k*

So the level of k* which maximises consumption is the level at which

MPK = δ + n

or, MPK – δ = n … (22)

This means that in the Golden Rule steady state, the net marginal (physical) product of capital equals the rate of growth of population.

The Solow growth model shows how saving and population growth conjointly determine the economy’s steady state capital stock and GDP per worker. It throws light on various features of actual growth experiences of advanced industrial countries.

It explains why high investment nations grow faster than low investment nations. It also explains why per capita incomes are low in countries with high rate of population growth.

However, the model fails to explain the persistent growth in living standards observed in most countries of the world — both developed and developing. In the basic Solow model, when the economy reaches its steady state, output per worker remains constant. To explain persistent growth, we have to incorporate the effects of technological progress in the model.

(B) Technological Progress:

The third source of economic growth is technological progress. It is called the residual factor of economic growth. If 51% of a country’s economic growth is due to capital accumulation and growth of the labour force then 49% of economic growth is the result of this invisible factor.

Since the effect of technological progress on economic growth can only be described and cannot be measured, it is known as a measure of our ignorance.

We may now incorporate this factor into the Solow model. It may be noted at the outset that while the growth of factor inputs over time leads to an increase in output directly, technological progress increases output indirectly, i.e., by raising the productivity of existing resources.

Technological progress alters the relationship between inputs (capital and labour) and the output of goods and services and thus leads to exogenous increases in society’s capacity to produce. It leads to intensive growth by shifting the production function upward.

Efficiency of Labour:

Since technological progress improves the efficiency of labour the production function may now be expressed as

Y = F(K, L x E)

where E is efficiency of the labour force, which is essentially a reflection of a society’s knowledge about the methods of production. With an improvement in technology, the efficiency of labour rises.

Since increases in the efficiency of labour (E) have the same effect on output as increases in the labour force (E), the product of the two (L x E) measures the number of effective workers. So total product (y) now depends on the number of units of capital (K) and the number of effective workers (L x E), where E measures the efficiency of each worker.’

Here we assume that technological progress causes the efficiency of labour E to grow at some constant rate g. This is an example of labour-augmenting technological progress and g measures the rate of such progress. Since the labour force (L) is assumed to increase at the rate n, and the efficiency of each unit of labour (E) is growing at the rate g, the number of effective workers (L x E), is growing at the rate n + g.

The Steady State with Technological Progress:

The effect of technological progress is the same as that of population growth because it is labour-augmenting in nature. Now we assume the number of effective workers to rise and describe the growth of the economy in terms of quantities (output levels) per effective worker.

Let k = K/(L x E) denote capital per effective worker, and y = Y/(L x E) denote output per effective worker. If the efficiency of labour is growing, then k and y refer to quantities per effective worker.

In the presence of technological progress we have the following relation which shows how k grows over time:

Δk = sf(k) – (δ + n + g)k

Thus the change in the capital stock Δk equals actual investment sf(k) minus the break­even investment (δ + n + g)k. Now, since k = K/LxE, break-even investment includes a new term, viz., gk, which is needed to provide capital for the new ‘effective workers’ created by tech­nological progress.

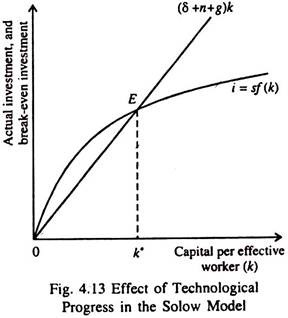
As shown in Fig. 4.13 even in the presence of technological progress there is one level of k, viz., k*, which ensures the existence of steady state. See at this level of k, both capital per effective worker and output per effective worker remain constant. As in the basic Solow model, this steady state represents the long-run equilibrium of the macro-economy.

The Effect of Technological Progress:

In the presence of technological progress, increases in the number of effective workers tend to decrease k. In the steady-state, investment i = sf(k) fully neutralises the reduction in k caused by depreciation, population growth and technological progress, i.e.,

Sf(k) = δk + nk + gk

The Criterion for the Golden Rule:

In the presence of technological progress the golden rule level of capital is defined as the steady state that maximises consumption per effective worker. Steady-state consumption per effective worker is

c* =J(k*) – (δ + n + g)k*

This is maximised if

MPK = δ + n + g

or, MPK -5 = n +g

This means that, at the Golden Rule level of capital, the net marginal physical product

of capital (net of depreciation), i.e., MPK – δ, must equal the rate of growth of total output which is the sum-total of growth of the labour force (n) and the rate of exogenous (labour- augmenting) technological progress (g).

This criterion can be used to evaluate whether actual economies (which experience both population growth and technological progress) have more or less capital than at the ideal situation, i.e., the Golden Rule steady state. Labour-augmenting technological progress affects the Solow model in the same way as population growth does.

Table 4.1 shows the behaviour of four key variables in the steady state with technological progress:

We know that capital per effective worker (k) is constant in the steady state. Moreover, since y = f(k), output per effective worker is also constant. Though the efficiency of each worker is growing at the rate g, output per worker (Y/L = y x E) also grows at the rate g. Total output [Y = y x (L x E)] grows at the rate n + g.

Implication of the Solow Model with Technological progress:

With the incorporation of technological progress, the Solow model can finally explain much of the observed sustained increases in the standard of living in the world around. While technological progress can lead to sustained growth in output per worker, a high rate of saving leads to a high rate of growth only until the economy attains a new steady state.

As soon as the economy reaches the steady state the rate of growth of output per worker depends only on the residual factor of growth. According to the Solow model, only continuous technological progress can explain the persistently rising living standard throughout the world.