Quantity Theory of Money (Equations) | Economics

Equations for quantity theory of money by different economists!

1. The Cambridge Equation:

The Cambridge economists explained their cash-balance approach to the quantity theory of money by formulating equations known as Cambridge equations.

The Marshallian cash-balance equation is expressed as follows:

M = KPY

where,

M is the quantity of money (currency plus demand deposits);

P is the price level;

Y is aggregate real income; and

K is the proportion of the real income which people desire to hold in money form.

Thus, using this equation, the value of money (I/P) is found out by dividing the total amount of goods which the people want to hold out of the total income (KY) by the amount of cash held by the public (M). Thus,

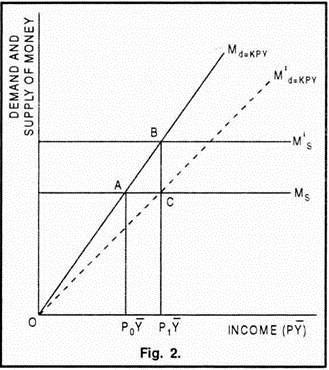
The cash balance approach implies that the price level (P) is directly proportional to the money supply (M) and indirectly proportional to the aggregate real income (Y) and the proportion of the real income which individuals choose to keep in the form of money (K). M and Y being constant, P falls with the increase in K and P rises with the decrease in K. Similarly, K and Y remaining unchanged, if M increases, P rises and if M decreases, P falls. These, conclusions of the cash-balance approach are illustrated in Figure 2.

In Figure 2, the supply of money curve (M_s) is a horizontal line indicating that the money supply is exogenously fixed by the monetary authority and is not influenced by the income level. M_d is the demand for money curve drawn as a function (K) of real income (Y). Real income has been assumed to the constant (Y̅). Initially, the supply and demand for money are equal at point A where the nominal income level is P₀Y̅.

Given the demand for money (M_d = KPY), an increase in the money supply from M_s to M’_s will create an excess of supply of money over the demand for money at the old income (P₀Y̅). As a result, the individuals will rid themselves of excess money balances by increasing their spending on goods.

Because the output (or the real income) is constant (i.e., Y̅), the increased money expenditures cause the price level to rise from P₀ to P₁ and the nominal income increases from P₀ Y̅ to P₁Y̅. Thus, by assuming K and Y as constant and setting M_d = M, the Cambridge equation yields the classical quantity theory of money and prices.

Similarly, assuming the money supply (M_s) to be given, a decrease in the demand for money as a result of decrease in K (say from 1/2 to 1 /3) causes a shift in the demand for money curve from M_d = KPY to M’_d = KPY. This creates an excess of the supply of money over the demand for money which, in turn, will increase spending on goods. Again, output being constant, this increased money expenditure will raise only the price level from P₀ to P₁ and hence the nominal income level from P₀ Y̅ to P₁ Y̅.

2. Pigou’s Equation:

Pigou’s cash-balance equation is as follows:

where,

P is the price level and 1/P is the purchasing power;

R is the total real income or the real resources;

K is the proportion of real income held by the people in the form of money; and

M is the total money supply

Since money is held by the community not merely in the form of cash but also in the form of bank deposits, Pigou extended his equation by dividing cash into two parts, i.e., cash with the public and deposits with the banks.

Thus his modified equation:

Pigou has given his equation in the form of purchasing power (1/P). According to him, K was more important than M in explaining changes in the purchasing power of money. This means that the value of money depends upon the demand for money to hold cash balances. Moreover, assuming K and R (and also c and h in the modified equation) to be constant, there is direct and proportional relationship between money supply (M) and price level (P).

3. Robertson’s Equation:

Robertson’s cash-balance equation is similar to that of Pigou but with a slight difference that in place of Pigou’s real resources (R), he includes total transactions (T).

Robertson’s equation is as follows:

M = KPT

where,

P is the price level;

M is the money supply;

T is the total amount of goods and services to be purchased during a year; and

K is the proportion of T which people wish to hold in the form of cash.

The equation clearly shows that P changes directly with M and inversely with K and T. Robertson’s equation is generally preferred to that of Pigou because it is easily comparable with Fisher’s equation.

4. Keynes Equation:

Keynes gives his real-balance quantity equation as an improvement over the other Cambridge equations. According to him, the demand for money is with reference only to consumer goods. In other words, people hold money to buy or to represent only goods and services.

Keynes’ equation is as follows:

Again, assuming k, k’ and r to be constant, the same conclusion emerges, i.e., there is direct and proportionate relationship between n and p.