How to Derive the Law of Demand ?

This article will guide you about how to derive the law of demand from the simple utility analysis of Marshall.

The law of demand now can be easily derived from this simple utility analysis of Marshall. Let’s again take the help of our example as given in Table 5.1.

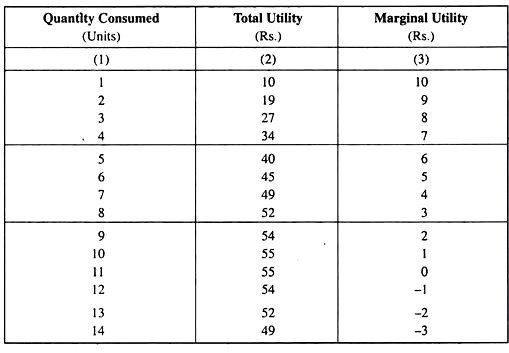
Table 5.1: Total and Marginal Utility Schedule of a Consumer in the Consumption of a Particular Good

At p = 7, the consumer will buy or demand 4 units of the good.

Now suppose that price comes down from Rs 7 to Rs 5. As this happens, equilibrium quantity demanded does not remain q = 4. For at q = 4, MU = 7 now becomes greater than p = 5, i.e., the consumer now earns a surplus utility of Rs 2 on the marginal unit or the 4th unit.

So he would now decide to increase his purchase to q = 6 because at this q, MU again falls to the level of p (MU = p = 5). Therefore, as p falls, consumer’s demand for the good rises.

Similarly, if p rises from Rs 7 to Rs 9, q = 4 no longer remains the equilibrium quantity, because now MU = 7 becomes less than p = 9, making the surplus utility on the marginal (4th) unit negative. So the consumer would now decide not to purchase the 4th unit.

In fact, he would decide to reduce his purchase to 3 units, because, at q = 3, MU rises to the level of p (MU = p = 9). Therefore, as p rises, consumer’s demand for the good falls. So here it will able to deduce a law.

This law, known as the (Marshallian) law of demand, states that as the price of a good falls or rises, other things remaining constant, the consumer’s demand for it would rise or fall, respectively.

The “other things” mentioned here are those that might also change to influence the consumer’s demand for the good. Some examples of these “other things” are consumer’s income, his tastes and habits, prices of some other (related) goods, etc.

With the help of the example, how the law of demand can be deduced from the Marshallian utility analysis in the single commodity case. A more formal analysis may be given in this way.

In the single commodity case, the consumer will purchase the quantity of a good at which the condition MU = p is satisfied, for then he would be able to maximise the surplus utility obtained. It may be remembered, p is the price of the good which is given and constant in the market.

The consumer cannot change or influence this price. If now p falls, MU would become greater than p, at the initial equilibrium point. The consumer now would come to enjoy a positive surplus utility on the margin.

In order to obtain the maximum of surplus, the consumer now would decide to demand a larger quantity of the good—the quantity at which MU would fall to the level of p. Similarly, if, at the initial MU = p point, price of the good rises, MU would be less than p, making the consumer obtain a negative surplus on the margin.

In order to maximise the surplus, the consumer now would be reducing q till MU rises to the level of p. Hence, the law of demand is obtained which is nothing but an inverse relationship between the price of a good and its quantity demanded.