Methods for Taking Investment Decisions under Risk

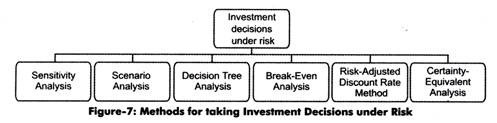
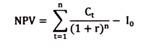Some of the most important methods that are used for taking investment decisions under risk are as follows:

1. Sensitivity Analysis 2. Scenario Analysis 3. Decision Tree Analysis 4. Break-Even Analysis 5. Risk-Adjusted Discount Rate Method 6. Certainty-Equivalent Analysis.

Risk refers to the deviation of the financial performance of a project from the forecasted performance. One needs to forecast the cash flows and other financial aspects while selecting a project.

However, the actual financial performance of a project may not in accordance to the forecasted performance. These risks can be decline in demand, uneven cash flow, and high inflation. For example, an organization is planning to install a machine that would increase the production level of the organization.

However, the demand of the product may vary with the economic environment, for example, the demand may be very high in economic boom and low if there is recession. Therefore, the organization may earn high income or incur huge loss, depending on the business environment.

However, different kinds of risks can be assessed up to a certain limit.

The risks can be assessed by using various methods that are shown in Figure-7:

1. Sensitivity Analysis:

Forecasting plays an important role in project selection. For example, a project manager needs to forecast the total cash flow of a project. The cash flow depends on the revenue earned and cost incurred in a project.

The revenue earned from the project depends on various factors, such as sales and market share. Similarly, if we want to find out the NPV or IRR of the project, we need to make the accurate predictions of independent variables. Any change in the independent variables can change the NPV or IRR of the project.

In sensitivity analysis, we analyze the degree of responsiveness of the dependent variable (here cash flow) for a given change in any of the dependent variables (here sales and market share). In other words, sensitivity analysis is a method in which the results of a decision are forecasted, if the actual performance deviates from the expected or assumed performance.

Sensitivity analysis basically consists of three steps, which are as follows:

1. Identifying all variables that affect the NPV or IRR of the project

2. Establishing a mathematical relationship between the independent and dependent variables

3. Studying and analyzing the impact of the change in the variables

Sensitivity analysis helps in providing different cash flow estimations in three circumstances, which are as follows:

a. Worst or Pessimistic Conditions: Refers to the most unfavorable economic situation for the project

b. Normal Conditions: Refers to the most probable economic environment for the project

c. Optimistic Conditions: Indicates the most favorable economic environment for the project

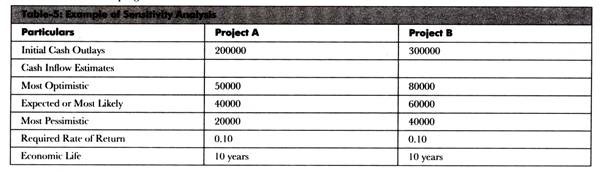
Let us consider the example given in Table-5:

Now, the NPV of each of the projects can be calculated by using the formula of NPV.

The calculation of the NPV of project A is shown in Table-6:

Similarly, the calculation of NPV of project B is shown in Table-7:

Therefore, we can see that the extent of loss in project B is less than that of project A but the extent of profit in project B is more than that of project A. Therefore, the project manager should select project B.

2. Scenario Analysis:

Scenario analysis is another important method of estimating risks involved in a project. It involves assessing future uncertainness associated with a project and their outcomes. In this method, different probable scenarios are analyzed and the associated outcomes are also determined.

For example, you are going to undertake an important project and have forecasted your cash flows accordingly. If your forecast goes wrong substantially, the future of the whole project can be jeopardized. As discussed earlier, in sensitivity analysis, different factors of a project are interdependent.

Therefore, if any of the factors are disrupted, the whole forecast can be wrong. Scenario analysis helps a project manager in preparing a framework where he/she can explore different kinds of risks associated with a project. It is more complex as compared to sensitivity analysis.

Scenario analysis needs sophisticated computer techniques to effectively calculate a large number of probable scenarios and their respective outcomes. Scenario analysis is more useful to a project manager than the sensitivity analysis as the former is more comprehensive and gives more insight about a project.

However, there are few disadvantages of this method, which are as follows:

(a) Complex Process:

Involves difficult calculations as calculating the NPV of a project is not easy by following this method. The complexity of the method makes it both costly and time consuming.

(b) Difficulty in Assessing the Probability:

Implies that it is very difficult to estimate the possibility of different outcomes. Sometimes, in practical life, assessing future uncertainties is not accurate.

3. Decision Tree Analysis:

Decision tree analysis is one of the most effective methods of assessing risks associated in a project. In this method, a decision tree is drawn for analyzing the risks associated in a project. A decision tree is the representation of different probable decisions and their probable outcomes in a tree-like diagram.

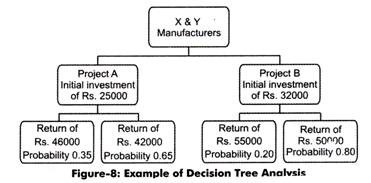
This method takes into account all probable outcomes and makes the decision making process easier. Let us understand decision tree analysis with the help of an example, X&Y Manufacturers has two projects, project A and project B. The two projects need the initial investment of Rs. 25000 and Rs. 32000, respectively.

According to an estimation, 35% probability of project A to give a return is Rs. 46000 in next five years and 65% probability is that it may give a return of Rs. 42000 in the same period. Similarly, 20% probability of project B to give a return of Rs. 55000 in next five years and 80% probability is that it may give a return of Rs. 50000 in the same period.

Now, if we express the problem in a decision tree, we will get a tree-like diagram, which is shown in Figure-8:

Now, the net value of each of the projects can be easily calculated. The net value of the project A would be (46000×0.35) + (42000×0.65) -25000 = (16100+27300-25000) =18400

Similarly, the net value of the project B would be (55000×.20) + (50000×.80)-32000 = 19000

Now, it is obvious that the project B is more profitable for the organization. Therefore, the organization should continue with project B.

The advantages of decision tree analysis are as follows:

(a) Detail Insight:

Provide a detailed view of all the probable outcomes associated with a project

(b) Objective in Nature:

Provides a clear evaluation of different alternative decisions

Following are the disadvantages of decision tree analysis:

(a) Difficulty in Large Number of Decisions:

Signifies that if the expected life of the project is long and the number of outcomes are large in numbers, it is quite difficult to draw a decision tree

(b) Difficulty in Interdependent Decisions:

Indicates that the calculation becomes very time consuming and complicated in case the alternative decisions are interdependent

4. Break-Even Analysis:

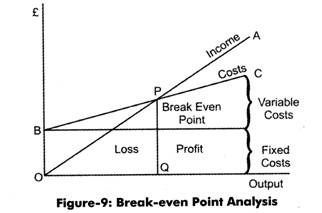
Break-even analysis is a widely used technique in project management. Break-even is a no profit and no loss situation for a project. In break-even analysis, all costs associated with a project are divided into two heads, fixed costs and variable costs.

The total fixed cost and the total variable cost are then compared with the total return or revenue of the project. In a break­even scenario, the total of all fixed costs or variable costs in a project is equal to the total revenue or return from the project. Therefore, a project can be said to have reached its break-even when it does not have any profit or loss.

The concept of breakeven point is explained in Figure-9:

The different costs used in break-even analysis are explained as follows:

(a) Fixed Costs:

Refer to the costs incurred at the initial stage of the project and does not depend on the production level or operation level of the project. For example, cost of a machinery and rent.

(b) Variable Costs:

Refer to the costs that depend on the volume of production. Wages and raw materials are the examples of variable costs.

(c) Total Cost:

Refers to the sum total of fixed costs and variables costs.

As shown in Figure-9, at point P, the total cost is equal to the total revenue. Therefore, the project can be said to have achieved break even at point P.

5. Risk-Adjusted Discount Rate Method:

Risk-adjusted discount rate method refers to the adjustment of risk in valuation model that is NPV.

Risk-adjusted discount rate can be expressed as follows:

d = 1/ 1+r+µ

Where, r = risk free discount rate

µ = risk probability

The preceding formula can be used for calculating risk-adjusted present value. For example, if the expected rate of return after five years is equal to R₅, then the risk-adjusted present value can be determined with the help of the following formula.

Present Value (PV) = 1/ (1+r+µ) ⁵ R₅

The calculation of risk-adjusted NPV for nth year can be done with the help of following formula:

Where, R_n = return in nth year

C_o = original cost of capital

By substituting the value of d, we get the following equation:

Let us understand the calculation of risk-adjusted discount rate with the help of an example. For example, a project, ABC cost Rs. 100 million to an organization. The project is expected to give a return of Rs. 132 million in one year. The discount rate for project 18% and probability of risk is 0.12. Find out whether the organization should accept the project ABC or not?

Solution:

The risk-adjusted NPV for project ABC can be calculated as follows:

Where, R = Rs. 132 million

C_o = Rs. 100 million

r = 0.08

H = 0.12

After substituting the given values of different variables, we get the risk-adjusted NPV that is equal to:

NPV = 132/1+0.08+0.12 = 100

NPV = 10 million

Therefore, the organization is getting risk-free return of Rs. 10 million.

If we calculate NPV for the same project, it would be equal to:

NPV = 132/1+0.08 = 100

NPV = 22.22 million

NPV and risk-adjusted NPV both are greater than zero. Therefore, project is profitable and should be accepted.

The advantages of risk-adjusted discount rate method are as follows:

(a) Changing discount rate by changing risk factor (µ) for different time periods and amount of risk

(b) Adjust the high risk of future by increasing the time duration for risk adjusted rate. For example, the risk-adjusted discounted rate for 50^th year is equal to:

(c) Regarding as the easiest method for evaluating projects in risk conditions

However, the disadvantage of risk-adjusted discount rate method is that it fails to provide tool for measuring risk factor. Therefore, it is required to be supplemented with the method to calculate risk factor.

6. Certainty-Equivalent Analysis:

Certainty-equivalent analysis is also used for the adjustment of NPV, thus, selecting or rejecting a project. It is similar to risk- adjusted discount rate analysis. However, there is one difference between them. In risk-adjusted discount rate analysis, the discount rate is adjusted while in certainty-equivalent analysis, expected return is adjusted.

Certainty-equivalent NPV can be, calculated with the help of the following formula:

NPV= aRn/ (1+ r) ⁿ-C₀

Where, a= certainty- equivalent coefficient

The value of a can be determined with the help of following formula:

α = R_n/R_n^*

Where, R_n = Expected certain return

R_n^* = Expected risky return

For example, between two projects P and Q, P is risky but gives Rs. 100 million of return after one year. However, Q is risk-free but gives Rs. 90 million of return after one year. The investment for project P is Rs. 70 million and for Q it is Rs. 73 million. The risk-free discount rate is 10%. In such a case, two projects are equal for the investor. This implies that risk-free project Q is equivalent to risky project P.

Therefore, certainty-equivalent coefficient would be:

α = 90/100

α = 0.9

The certainty-equivalent NPV for project P would be:

NPV= α R_n/ (1 + r) ⁿ –C₀

NPV = 0.9 * 100/ (1+0.1) -70

NPV = 12 million

The certainty-equivalent NPV for project Q would be:

NPV = R_n/ (1+r) ⁿ – C₀

NPV = 90/ (1+0.1) – 73

NPV = 9 million

The project P yields more with less investment as compared to project Q. Therefore, project P would be selected.