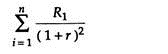Changes in Rates of Interest and Investment Decisions

The following article will guide you to learn about how does changes in rates of interest affects investment decisions of business firms.

Investment refers to a change in the stock of capital of a firm between two periods. The term is most commonly used to describe the flow of expenditures devoted to increasing or maintaining the real capital stock. In fact, a more accurate definition is that, investment is the flow of expen­ditures devoted to projects producing goods which are not intended for immediate consumption.

These investment projects may take the form of adding to both physical capital as well as inventories. Investment is a flow, the volume of which is determined by all those projects which yield a positive net present value, or an internal rate of return, greater than the interest rate. The former is known as the net present value criterion and the latter as the marginal efficiency of investment criterion.

The rate of interest is an important variable affecting the level of (planned) investment expenditure. The fundamental point here is that investments are undertaken up to the point at which the marginal invest­ment is expected, over the lifetime of an asset, to yield returns which just cover the cost of the investment. This ‘break-even’ investment is the cut-off point for the investor.

If investment projects are ranked according to the net returns (i.e., return over cost) which they yield, those above the break-even investment will yield net returns to the investor and those below would, if they were undertaken, yield net losses. Clearly, in order to specify the critical point it is necessary to identify the expected returns and costs which enter the investor’s decision making process.

To start with, it should be clear that Re 1 received now is worth more than Re 1 received in a later period, since the earlier the money is received the more future interest the lending of that money can accumulate. If V₀ is a sum of money lent in period O, then the capital sum of period 1 is V₀ (1 + r) where r is the rate of interest received.

Lending out again this larger capital sum and receiving interest on it for period 1 produces a capital sum in period 2 of [V₀ (1 + r) (1 + r)] = V₀ (1 + r)] ² and if the same process is repeated the capital sum of period 3 is [V₀ (1 + r) ²] (1 + r) = [V₀ (1 + r)] ³ so that the capital sum accumulates over j periods according to the progression

V₁ = V₀ (1 + r) ¹ … (1)

The conclusion is that a sum V₀ owned in period O will be worth more than V₀ in a future period; and it follows that a sum V₀ which is not owned until a future period must be worth less than V₀ owned in period O.

If money is received in the present we accumulate the interest to find the future value; but if money is received in the future we discount it to find the present value.

From equation (1) it is apparent that the present value V₀ of a future value V₁ is:

V₀ = V₁ / (1 + r) ¹ … (2)

The investor, when considering a particular investment project, will have some idea of the stream of future returns (earnings) he expects to accrue to the real asset.

For the years 1,2,…, n, of the life of the asset the net returns are, in terms of their value at the time they are received (i.e., in current values):

R₁ R₂,…,R_n …(3)

To find the present value of all expected returns we must apply the discounting procedure to every future return R₁.

Consequently, using equa­tion (2) the stream of returns (3) has a present value of:

The investor compares this present value of returns with the cost of the real asset P^c which is incurred in period O.

The condition for the maximisa­tion of net return over cost is that increments of investment continue, until at the margin:

That is to say, until marginal investment has a present value of expected returns which just covers the initial cost. Since investment as a whole is assumed to be subject to diminishing marginal returns, if (5) is satisfied, there necessarily exist intra-marginal investments which yield net returns and which are therefore undertaken.

We now consider the effect of changes in the rate of interest. An increase in r raises the return .on a sum of money lent and therefore increases the rate of accumulation of the capital sum. Consequently, an increase in r leads to future returns being discounted more heavily than before. If R₁ R₂,…, R_n are unaltered then this heavier discounting reduces

because of the increase in the size of the denominator. Since the cost of the real asset remains the same, a reduction in the present value of returns in equation (5) means that the previously marginal investment now fails to cover its cost, i.e.,

The consequence is that this now extra-marginal investment is not un­dertaken. The level of investment planned is cut back to the point at which the returns at the margin just cover costs again; this means that a previously intra-marginal investment which yielded net returns now becomes the break-even investment, i.e., the marginal investment, and some less produc­tive investments are abandoned.

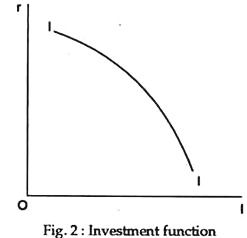
The implication of the argument is that the level of planned investment is a negative function the rate of return on financial assets, r:

I = f (r)

where (dl/dr) < 0. This investment func­tion is shown in Fig. 2.

It can be argued that investment plans will be responsive to changes in the rate of interest down to a certain level of the rate of interest but will be completely interest- inelastic at lower rates of interest. In truth, at low rates of interest the opportunity cost of an investment is small anyway and marginal adjustments in the rate will not alter the investment decision which be­comes dominated by the uncertainties associated with the expectations of future earnings.

If this were true then the investment function in Fig.2 would become vertical below a certain rate of interest since below this rate:

dI/dr = 0

R.G. Lipsey has pointed out that major changes in interest rates are often associated with changes in investment. Most econometric studies, however, show a weak relation in the sense that changes in the rate of interest cause relatively small changes in the amount of investment.

Conclusion:

It may now be noted that individual firms’ MEC schedules can be aggregated to obtain the relationship between the interest rate and aggregate investment. This is the type of investment function generally assumed in both classical and Keynesian models. The major difference between these has to do with the interest elasticity of the investment function.

Keynes believed that this was small because the function was dominated by uncertain future cash flows, while classical economists be­lieved that investment was sensitive to changes in interest rates. The issue is important for economic policy — if investment is not sensitive to interest rates the ability of monetary policy to affect investment through interest rate changes is limited.