The following points highlight the two main approaches for determining devaluation of currency. The approaches are: 1. The Elasticity Approach 2. Absorption Approach.
1. The Elasticity Approach:
In fact, the success of devaluation in improving the balance of trade position of a country depends on the fulfilment of a condition known as the Mar- shall-Lerner condition. In fact, this condition is stated in terms of the price-elasticity of demand for imports and exports it is called the elasticity approach.
Specifically, the elasticity values for a successful devaluation are:
ADVERTISEMENTS:
(i) Demand for exports is price-elastic (ex ≥ 1)
(ii) Demand for imports is price-elastic (em ≥ 1)
The degree of success of devaluation thus depends on the reaction of import and export volumes to the changes in prices implied by the devaluation. If the values of trade are relatively elastic to price changes, then devaluation will be successful; that is, an increase in import prices results in more than proportionate fall in import volume, reducing the total amount of foreign currency required to finance the import bill. At the same time the fall in the price of exports results in a more than proportionate increase in total foreign currency earnings on exports. The converse is also true.
However, certain other factors also influence the final outcome of a devaluation, in particular the extent to which domestic resources are sufficiently mobile to be switched into export producing and import-substituting industries.
ADVERTISEMENTS:
The J-Curve:
Floating exchange rates do not guarantee immediate changes in international trade accounts that will corrected balance-of- payments deficits in any country. In principle, if a country is having a balance-of-trade deficit, there should be a depreciation of that country’s currency and an improvement in its balance of payments.
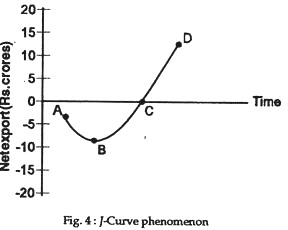
This happens, but only slowly. Indeed, even after depreciation a country’s net export position may continue to deteriorate. How can this be? The explanation comes from the phenomenon called the J-curve. It shows a situation following a depreciation in a country’s currency value internationally. After the depreciation, there is a worsening of the country’s foreign trade deficit and only some time later an improvement in its balance of trade position.
Fig. 4 shows a J-curve. Net exports (exports minus imports) are measured on the vertical axis; time is on the horizontal axis. According to the J curve if we start at point A, we have to go down to point B with a worsening of the balance of trade deficit until we start to move back up to balance at point C. Point C is the situation in the long run. All previous points on the J curve are representative of balance of trade deficits in the short run that occurred just after depreciation of a country’s currency.
The explanation of the J-curve phenomenon has to do with the price elasticity of the demand for imports in the short run. As it turns out, import demand price elasticity is relatively low—imports are not immediately very responsive to a change in price.
That means that as the rupee depreciates the increased relative price of imports does not cause Indians to cut back very much on their consumption of imported goods. Suppose the price of imports increases by 20% but the quantity demanded falls by only 10% The total expenditures on imports will go up, not down. The balance of trade deficit will increase.
Not surprisingly, the existence of the J-curve phenomenon has been taken by some economists to mean that the system of flexible exchange rates is undesirable. Because of the J-curve phenomenon, it can be said that changes in exchange rates are a somewhat crude way of solving a balance of trade deficit.
An alternative approach to devaluation is the absorption approach.
2. Absorption Approach:
From an analysis of Keynesian model we know that the total income of a nation can be expressed in the following manner:
Y ≡ C + I + G + X — M
where Y represents income, C consumption, I investment, G government expenditure, X exports and M imports.
This relationship can be shortened by merging the first three terms of the expression (on the right hand side), i.e., by calling C + I + G by the name ‘absorption’ or A. The two remaining terms S — M, the difference between exports and imports, constitute the trade balance and can be denoted by B We can, therefore, write:
Y ≡ A + B
ADVERTISEMENTS:
So the trade balance must always be the difference between income and absorption:
B ≡ Y—A
The balance of trade would be negative if A, i.e., absorption is greater than income—that if the nation absorbs more than it produces. The trade balance can improve if income increases while absorption increases less or stays unchanged or falls; or, if absorption decreases while income decreases less or stays unchanged.
So the problem concerns the extent to which a certain depreciation (of say 10%) affects B, that is, the difference between income and absorption. The change in trade balance is the change in income minus the change in absorption; or,
ADVERTISEMENTS:
ΔB = ΔY—ΔA
The income effect of devaluation will be reflected in d, the effect of change in income upon absorption and the direct effect upon absorption will both be reflected in ΔA. There will thus be an income-induced change in A and a direct or non-income induced change in A. The direct change in A can be expressed in δA, and if we use symbol α to mean “the marginal propensity to absorb income, the income-induced change in absorption can be expressed as αΔY.
We can now combine the devaluation effect upon income, ΔY, and the income effect upon absorption, αΔY, into a single expression, (1—α) ΔY, which stands for the non-absorbed change in income. Thus
ΔB = (1—α) ΔY—δA.
ADVERTISEMENTS:
If we assume that income increases as a result of devaluation (through a rise in exports by the foreign trade multiplier), then the consequent effect upon absorption can improve balance of trade only if α is less than unity. But although the marginal propensity to consume alone is likely to be less than unity, the combined marginal propensities to consume, invest and spend publicly is less likely to be so.
If α has a value equal to unity, there will be no improvement in the balance of trade. If a is greater than unity, there will actually be deterioration in the balance of trade. Only the direct effect on absorption, therefore can help matters.