Nash Equilibrium Strategies of Game Theory | Microeconomics

The definition of Nash equilibrium lacks the ∀ s-i” of dominant strategy equilibrium. The Nash equilibrium strategy need only be a best response to the other Nash strategies not to all possible strategies. Although, we deal with best responses and the moves are actually simultaneous. Therefore the players are predicting each other moves.

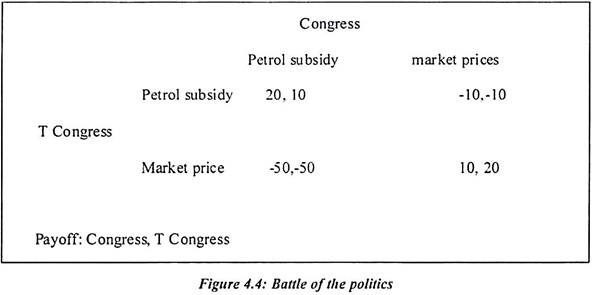
The Battle of Politics:

In the battle of politics, we have assumed that there are two political parties maximizing their payoffs. Such payoffs are useful to get majority in election. In India, no party gets the majority at center. Therefore coalition government is the only way to form the government. Coalition politics is different than the one party dominant politics/strategy. In coalition government, different parties have different manifesto and they do not compromise on it. But policy formation at national level can affect the manifesto of local parties. Therefore the local party may oppose the policies of the national party.

In India, we found that the Trinamool congress party always opposes the Congress on different issues. Trinamool congress party is a local political party in West Bengal. We have taken the example of the petrol prices. The hike in petrol prices is continuously opposed by the Trinamool congress. In India, subsidy is given on the petrol. Now congress government is formulating the policies to reduce petrol subsidy. This is because to reduce the fiscal deficit at central level. Most of the government oil companies are determining the petrol prices.

Such prices are depending on the international petrol prices. If the price of petrol rises in international market then these companies have no choice but to increase the price of petrol. If it is not done so then the subsidy amount rises and it affects on fiscal deficit of government. Therefore government is involved in the price fixation of petrol. While doing this, government do not discuss and take the opinion of the other political parties. It sometime creates instability in coalition politics.

It is obvious that the political party like Trinamool Congress opposes such decision. If both parties will not agree to increase in price of petrol then the conflict among two parties will occur. The Nash equilibrium is sometimes justified by repetition of the game. Suppose the congress do not discuss with coalition parties and they repeat the game period after period then the problem of instability will occur in government. In this game, they eventually settle on one of the Nash equilibrium. But it depends on both preferences.

Each of the Nash equilibrium in the Battle of the politics is Pareto-efficient. There is no any other strategy combination increase the payoff of one party without decreasing that of the other. Congress Party moves first in deciding petrol prices. If the Congress Party increases the price of petrol then its commitment would induce the Trinamool congress to go to the way to increase the price of petrol. We have considered the price of petrol which increases per liter.

The petrol subsidy will benefit more to Trinamool congress rather than the (20, 10) Congress. But if the market price is accepted by the congress then the benefit are (10, 20) which are less to congress. But such efforts will help to smooth work of government and financial stability. If Trinamool congress support market price and congress go for petrol price hike then the benefit are (-50,-50) same for both parties.

In political games, the party who moves first has a first mover advantage. It is equivalent to commitment. The battle of politics has many economic applications. Such choices are widely used in industry. Suppose two firms have different preferences and both want a common standard to encourage consumers to buy the products. Second firm choose a language used in a contract those two firms want to formalize a sales agreement. But they prefer different terms.

In coalition government, political parties work together but they have different preferences. On the basis of political party manifesto, competition takes place among each other. Any political party which wins with majority in election emerges as the strongest party and form a government. It is simple game that political party with maximum number won seats takes decision at different levels of government.

The Normal Form and Outcome Matrix:

The game with several moves in sequence requires more care in presentation than single move games. The strategies are the same as actions in pure co-ordination and the outcomes are 2 by 2 form. It is related to strategy combinations to payoffs and action, outcomes. These two mappings are called the normal form and the outcome matrix and in more complicated game they are distinct from each other.

The normal form shows what payoff result from each possible strategy combination. The outcome matrix shows what outcome results from each possible action combinations. The definitions below use in to denote the number of players. Suppose k is the number of variables in the outcome vector and p is the number of strategy combinations and q the number of action combinations.

It is presented as follows:

The normal form of game consists as:

1. All possible strategy combinations are S where S₁……… Sn.

2. Payoff functions mapping Sⁱ on to the payoff n where πⁱ (I = 1,….n)

The outcome matrix consists of two outcomes:

1. All possible action combinations are a¹……. aⁿ

2. Outcome functions mapping a¹ into the outcome k where zⁱ, = (1,……… n)

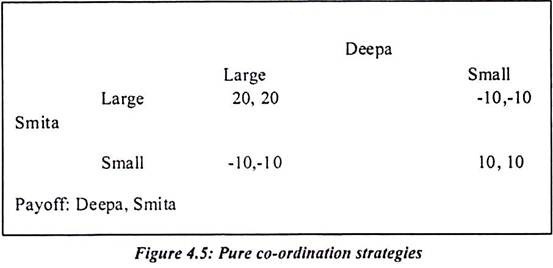
Pure Co-Ordination:

We have taken different examples for different kinds of games. The players in these games are Deepa and Smita. They are competitive players with each other and they want higher payoff out of their actions. Both would prefer large pay off out of individual strategy but their individual strategy is depending on each other.

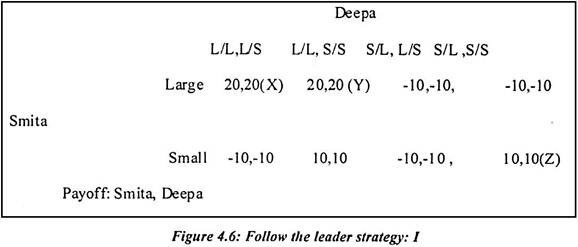
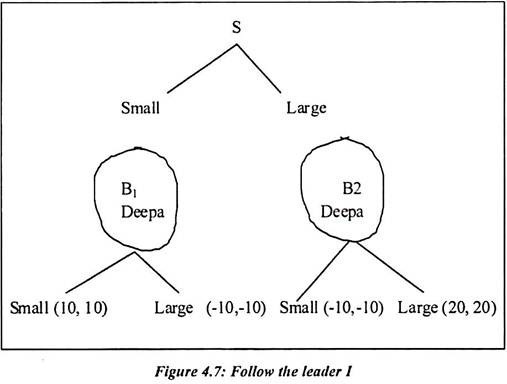
In the pure co-ordination game, follow the leader one principal strategy is applied. In this game, Smita moves first. She is committing herself to a certain disk size, no matter what Deepa chooses. The new game has an outcome matrix identical to pure co-ordination. It is a normal form of different games. This is because Deepa’s strategies are no longer single actions. Deepa’s strategy set has four elements.

Such strategies are explained as follows:

Which we will abbreviate as

Follow the leader illustrate that how adding a little complexity can make the normal form too unclear. But it is very useful.

From the above table, we have given equilibrium Strategy outcomes.

They are as follows:

X {Large (large, large)} both pick large

Y {Large (large, small)} both pick large

Z {Small (small, small)} both pick small

In the above box, X, Y and Z are Nash equilibrium strategies. In equilibrium X, Deepa will respond with large regardless of what Smita does so. Smita is quite happy to choose large. Deepa would be stupid to choose large if Smita choose small first. But that event will never happen in pure co-operative equilibrium. At equilibrium Y, Deepa will choose whatever Smita chooses. So Smita chooses large to make the pay off.

At this point, payoff 2 is better instead of 1. In equilibrium Z, Smita deliberately chooses small. This is because she knows that Deepa will respond with small whatever she does. Deepa is willing to respond with small because Smita chooses small in equilibrium. Equilibrium x and z are not completely sensible at this point.

The Extensive Form and Game Tree:

We use the extensive form and decision tree to solve the problem. The game tree is same as the extensive form. There is outcome at each node. Suppose the outcome out of equilibrium is defined as a payoff then the extensive form is equilibrium to the decision tree. We are interested to see why equilibrium X and Z are unsatisfied even though they are Nash equilibrium.

We need to understand it through decision tree.

It is as follows:

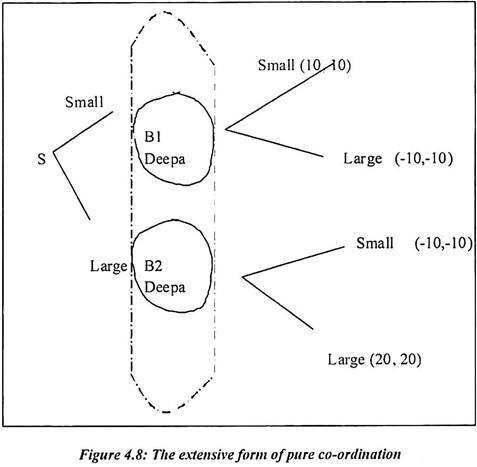
In the above figure 4.7, the game actually reaches at node of B1 or either B2. Deepa would have dominant action at B2. This is because the payoff is more. She would have small payoff at B1. As far as X and Z equilibrium are concerned, then the Nash equilibrium is observed at Y. The extensive form of pure co-ordination is presented in the figure. It shows that the dotted lines are the extensive form. It is a follow the leader 1 strategy.

In this game, each player makes a single decision between two actions. The movements of the players are simultaneous. Suppose Smita does not tell about her movement to Deepa and she moves first. Deepa understands her movement and the game reaches at some node. In the figure, such information set is marked by the dotted lines. But Deepa do not know at the exact node reached in this game.

Mixed Strategy: The Welfare Game:

In the game theory, Nash equilibrium is most desired outcome. Nash equilibrium is useful to provide predictions of outcome. It does not require dominant strategies. Some games do not have the Nash equilibrium. It is realistic and useful to expand the strategy space. It includes random strategy in which Nash equilibrium is almost and always exists. These random strategies are called mixed strategies.

A pure strategy maps each of a player possible information sets to one action,

A mixed strategy maps each of plays possible information sets to probability distribution actions

An expanded game theory version allows mixed strategies. It is called as the mixed extension of the game. A pure strategy is a rule that tells the other player and what action to choose. A mixed strategy constitutes a rule that tells him what dice to throw in order to choose as action. If a player pursues a mixed strategy, he might choose any of several different actions in a given situation. It is an unpredictability which can be helpful to him.

Such mixed strategy occurs frequently in the real world. In American football games, the offensive team has to decide whether to pass or to run. The passing generally gain more yards but what is most important is to choose an action which is not expected by their team. Teams decide to run part of the time and pass part of the time. It is in a way that seems random in observers but rational to game theorists.

The Welfare Game:

In a developing country like India, government sanctions number of welfare programs for poor people. We can call it as welfare state criteria or political economy but welfare programs are announced for poor people. Some welfare programs get popular because many people participate in such programs. Most of the time, people and local representatives demand such welfare programs. Welfare programs in India really help in creating different kind of rural infrastructure and sustain ecological environment.

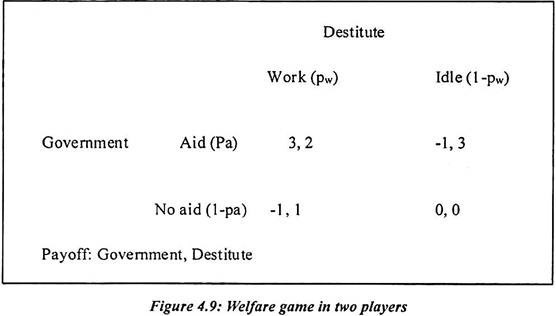
But some social welfare programs fail because of lower participation of rural people and time of policy intervention. In this welfare game, we have taken an example of the government and destitute. In the welfare game model, government wishes to aid a destitute. Such destitute is poor person of rural area and always search work at the nearest location. Now it is a dilemma whether destitute searches for work only if he cannot depend on government aid.

Destitute may not succeed in finding a job ever if he tries payoffs which represent this situation. In this game neither government nor destitute has a dominant strategy. Both are depend on each other for benefits. With some thinking, we can observe that there is no Nash equilibrium exists in pure strategies.

It is explained with the following example:

In the above example, each strategy combination must be examined in turn to check for Nash equilibrium.

The strategy combination (Aid, try to work) (Aid, be Idle) (No Aid, Be Idle) (No Aid, Try to work) is not Nash equilibrium.

The government plays Aid with probability Pa and the destitute try to work with probability Pw.

The governments expected payoff is:

If only pure strategies are allowed Pa equals zero or one. But in the mixed extension of the game, the government’s action of Pa lies on the continuum from zero to one. The pure strategies being the extreme values differentiate the payoff function with respect to the choice variable. It is to be obtaining the first order condition.

Above example shows that in the mixed strategy equilibrium, the rural destitute selects the option try to work 20 percent of the time to obtain the destitute strategy. The number of strategies and payoffs for government is explained as follows. Firstly, the optimal mixed strategy exists for the government. Secondly, suppose the destitute work more than 20 percent of the time then the government always selects Aid. But alternatively, if the destitute selects try to work less than 20 percent of the time, the government never selects Aid for work.

It is clear strategy for government to select aid for destitute. Thirdly, for government, the mixed strategy is that the destitute must select try to work with probability exactly 20 percent. In developing country like India, there is often demand of people to start work and it is expected that they are willing to spend time on government welfare program. If it is not so then it will be wastage of public resources. Now it is the government which decides whether to start the aid program or not. In order to obtain the probability of the government choosing Aid, we must calculate the payoff for destitute.

Such function is defined as follows:

If we take first order condition then:

Suppose the Destitute selects try to work with probability 0.2 then government is indifferent to select Aid. It is with probability 100, 0 or anything in between. In the mixed strategy of Nash equilibrium, government selects Aid with probability 0.5.The Destitute selects try to work with probability 0.2. The equilibrium outcome could be any of the four entries in the outcome matrix. The entries having the highest probability of occurrence are (no aid, be Idle) and (Aid, be Idle) each with probability 0.4 = 0.5 (1⎯ 0.2).

From the above probabilities we are not clear whether government will select the aid program for the destitute. Sometime work is demanded but destitute is not ready to work and prefer to remain idle. Therefore most of the time, there is evaluation of the aid. The aid is helping destitute then it is continued otherwise it gets stopped.

Sometimes effectiveness of the aid program is more important but it depends on number of things for example possibility of migration in urban and rural area, alternative job possibilities, learning new skills etc. Government evaluates such aid programs at different level and time. It is evaluated by independent research agencies. The aid is sanctioned after careful evaluation of various reports.

Co-Related Strategies:

Co-operative games encourage participation and collaboration. The co-related equilibrium strategies are the solution rather than the Nash equilibrium. Such strategy is firstly discussed by Mathematician Robert Aumann in 1974. He has pointed out that each player chooses action according to his/her observation. Such observations are the value of the same public signal. A strategy becomes action to every possible observation a player can make. Suppose not a single player would want to deviate from the standard strategy then the distribution is called as the co- related strategies.

A co-related equilibrium is given for two players as toss a coin. The strategies are simple for Smita and Deepa. Smita can choose stay if it comes up heads. For Deepa, she can choose stay if it comes up tails. For the player who loses the toss to choose the back movement. Each player’s strategy is a best response to the others. The probability of each choosing stay is half that is 0.5.

The expected payoff for each is 1.00. This is a simple probability function exists in this game. Usually the randomizing devise is not modeled explicitly when a model refers to correlated equilibrium. An extrinsic uncertainty refers to uncertainty over variables that do not affect preferences endowment or production.

In order to model co-related strategy outcome, we need to specify a move by nature. It gives each player with equal probability, the ability to commit first to an action such as stay. This is often realistic because it amounts to a zero probability of both players entering the industry at exactly the same time. But no one knows in advance who will be the lucky starter. Firm has no prior advantage but the outcome is efficient. The mixed strategies cannot be used for co-relation strategies. In an ordinary mixed strategy, the mixed probabilities are statistically independent. In co-related strategies they are not.

The cheap talk refers to costless communication before the game begins. In pure co-ordination, cheap talk instantly allows the players to make the desirable outcome. Without communication, the only symmetric equilibrium is mixed strategies. Suppose both players know that making inconsistent announcement will lead to be the wasteful mixed strategy outcome then they are willing to mix announcing whether they will go the ballet or the prize fight. Their chances of coming to an agreement are high.

Therefore communication can help to reduce inefficiency even if the two players are in conflict. But again such strategies are depends purely on the communication between two players. The goal is not to win as a player but as a team of players. Discovering effective cooperative game patterns is an elusive and important problem that is personal communication. Most of the time communication is the last strategy which is used as solution to the problem.