5 Types of Games in Game Theory (With Diagram)

Read this article to learn about the different Types of Games in Game Theory – explained with diagrams!

In the game theory, different types of games help in the analysis of different types of problems.

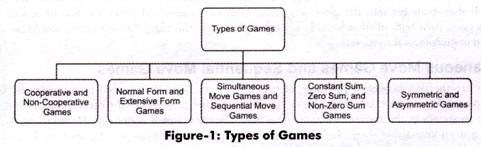
The different types of games are formed on the basis of number of players involved in a game, symmetry of the game, and cooperation among players.

The different types of games (as shown in Figure-1) are explained below:

1. Cooperative and Non-Cooperative Games:

Cooperative games are the one in which players are convinced to adopt a particular strategy through negotiations and agreements between players. Let us take the example cited in prisoner’s dilemma to understand the concept of cooperative games. In case, John and Mac had been able to contact each other, then they must have decided to remain silent. Therefore, their negotiation would have helped in solving out the problem.

Another example can be cited for pan masala organizations. Suppose pan masala organizations have high ad-expenditure that they want to reduce. However, they are not sure whether other organizations would follow them or not.

This creates a situation of dilemma among pan masala organizations. However, the government restricts the advertisement of pan masala on televisions. This would help in reducing the ad-expenditure of pan masala organizations. This is an example of cooperative game.

However, non-cooperative games refer to the games in which the players decide on their own strategy to maximize their profit. The best example of a non-cooperative game is prisoner’s dilemma. Non-cooperative games provide accurate results. This is because in non-cooperative games, a very deep analysis of a problem takes place.

2. Normal Form and Extensive Form Games:

Normal form games refer to the description of game in the form of matrix. In other words, when the payoff and strategies of a game are represented in a tabular form, it is termed as normal form games. Normal form games help in identifying the dominated strategies and Nash equilibrium. In normal form games, the matrix demonstrates the strategies adopted by the different players of the game and their possible outcomes.

On the other hand, extensive form games are the one in which the description of game is done in the form of a decision tree. Extensive form games help in the representation of events that can occur by chance. These games consist of a tree-like structure in which the names of players are represented on different nodes.

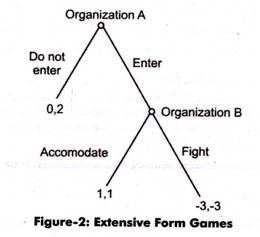
In addition, in this structure, the feasible actions and pay offs of each players are also given. Let us understand the concept of extensive form games with the help of an example. Suppose organization A wants to enter a new market, while organization B is the existing organization in that market.

Organization A has two strategies; one IS to enter the market and challenge to survive or do not enter the market and remain deprived of the profit that it can earn. Similarly, organization B also has two strategies either to fight for its existence or to cooperate with organization A.

Figure-2 shows the decision tree for the present situation:

In Figure-2, organization A takes the first step that would be followed by organization B later on. In case, organization A does not enter the market, then its payoffs would be zero. However, if it enters the market, the market situation would be totally dependent on organization B.

If they both get into the price war, then both of them would suffer the loss of 3. On the other hand, if organization B cooperates, then both of them would earn equal profits. In this case, the best option would be that organization A enters the market and organization B cooperates.

3. Simultaneous Move Games and Sequential Move Games:

Simultaneous games are the one in which the move of two players (the strategy adopted by two players) is simultaneous. In simultaneous move, players do not have knowledge about the move of other players. On the contrary, sequential games are the one in which players are aware about the moves of players who have already adopted a strategy.

However, in sequential games, the players do not have a deep knowledge about the strategies of other players. For example, a player has knowledge that the other player would not use a single strategy, but he/she is not sure about the number of strategies the other player may use. Simultaneous games are represented in normal form while sequential games are represented in extensive form.

Let us understand the application of simultaneous move games with the help of an example. Suppose organizations X and Y want to minimize their cost by outsourcing their marketing activities. However, they have a fear that outsourcing of marketing activities would result in increase of sale of the other competitor. The strategies that they can adopt are either to outsource or not to outsource the marketing activities.

The payoff matrix for the two organizations is shown in Table-10:

In Table-10, it can be seen that both the organizations X and Y are unaware about the strategy of each other. Both of them work on the perception that the other one would adopt the best strategy for itself. Therefore, both the organizations would adopt the strategy, which is best for them.

The same example can also be used for the explanation of sequential move games. Suppose organization X is the first one to decide whether it should outsource the marketing activities or not.

The game tree that represents the decision of organization X and Y is shown in Figure-3:

In Figure-3, the first move is taken by organization X while organization Y would take decision on the basis of the decision taken by X. However, the final outcome depends on the decision of organization Y. In the present case, the second player is aware of the decision of the first player.

4. Constant Sum, Zero Sum, and Non-Zero Sum Games:

Constant sum game is the one in which the sum of outcome of all the players remains constant even if the outcomes are different. Zero sum game is a type of constant sum game in which the sum of outcomes of all players is zero. In zero sum game, the strategies of different players cannot affect the available resources.

Moreover, in zero sum game, the gain of one player is always equal to the loss of the other player. On the other hand, non-zero sum game are the games in which sum of the outcomes of all the players is not zero.

A non-zero sum game can be transformed to zero sum game by adding one dummy player. The losses of dummy player are overridden by the net earnings of players. Examples of zero sum games are chess and gambling. In these games, the gain of one player results in the loss of the other player. However, cooperative games are the example of non-zero games. This is because in cooperative games, either every player wins or loses.

5. Symmetric and Asymmetric Games:

In symmetric games, strategies adopted by all players are same. Symmetry can exist in short-term games only because in long-term games the number of options with a player increases. The decisions in a symmetric game depend on the strategies used, not on the players of the game. Even in case of interchanging players, the decisions remain the same in symmetric games. Example of symmetric games is prisoner’s dilemma.

On the other hand, asymmetric games are the one in which strategies adopted by players are different. In asymmetric games, the strategy that provides benefit to one player may not be equally beneficial for the other player. However, decision making in asymmetric games depends on the different types of strategies and decision of players. Example of asymmetric game is entry of new organization in a market because different organizations adopt different strategies to enter in the same market.