Game Theory: An Overview | Microeconomics

Here we shall briefly discuss how the game theory can be used to study the economic behaviour in oligopolistic markets.

The Payoff Matrix of a Game:

Strategic interaction may involve many players and many strategies, but here we shall consider only two-person games with a finite number of strategies. This will enable us to present the game easily in a payoff matrix.

We may take help of a specific example to understand the subject. Let us suppose that two people are playing a simple game. Person A has only two strategies available and person B also has two. The total number of possible outcomes is, therefore, 2 x 2 = 4.

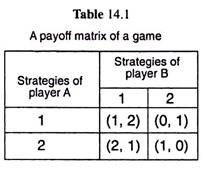
For each possible outcome there is a corresponding payoff to each player. Table 14.1 is the payoff matrix of the game. In this table, the pay-offs to two players are given in combinations.

The first entry in each combination represents the payoff to player A and the second entry gives the payoff to player B. For example, if both players adopt their respective first strategies the payoff combination will be (1, 2). Similarly, if A adopts strategy 1 and B adopts strategy 2, then the payoff combination will be (0, 1).

Let us now see what the outcome will be of this sort of game. This game, of course, has a very simple solution. From A’s point of view it is always better for him to adopt his strategy 2, since his payoffs from that choice (2 or 1) are always greater than the corresponding payoffs (1 or 0) from strategy 1.

Similarly, it is always better for B to adopt his strategy 1, since his payoffs from that choice (2 or 1) are always greater than the corresponding payoffs (1 or 0) from strategy 2. We would expect, therefore, that the equilibrium strategy for A is his strategy 2 and that for B is his strategy 1, and so, the equilibrium payoff combination here would be (2, 1).

We have a dominant strategy, i.e., one optimal choice of strategy for each player irrespective of what the other player does. It is seen in the payoff matrix of Table 14.1 that whichever choice of strategy B makes, A will get a higher payoff if he plays strategy 2, and so, it makes sense for A to adopt strategy 2.

On the other hand, whatever choice A makes, B will get a higher payoff if he adopts his strategy 1. Hence, here these choices of strategy, i.e., strategy 2 for A and strategy 1 for B dominate the alternative choices, and we have an equilibrium in dominant strategies.

In this example, we would expect, therefore, an equilibrium outcome where A plays his strategy 2 receiving an equilibrium payoff of 2, and B plays his strategy 1 receiving an equilibrium payoff of 1.

The Nash Equilibrium:

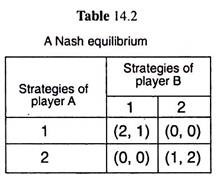
The game is rather easy to handle if we have a dominant strategy for each player, which, however, may not always be the case. For example, the game given in Table 14.2 does not have dominant strategies. Here, when B adopts his strategy 1, A gets a payoff of 2 (from strategy 1) or 0 (from strategy 2), and when B chooses strategy 2, the payoff to A is 0 (from strategy 1) or 1 (from strategy 2).

Thus, here when B adopts strategy 1, A will also play his strategy 1; on the other hand, when B plays his strategy 2, A would change his strategy from 1 to 2. Thus, A’s optimal choice depends on what he thinks B will do. In other words, there is no dominant strategy for A in this case. Neither does B have a dominant strategy here.

For, as we see in the payoff matrix, when A chooses strategy 1, B will choose his strategy 1 and when A chooses strategy 2, B will change from his strategy 1 to strategy 2. That is, B also has no dominant strategy here. His optimal choice would depend on what he thinks A will do.

Therefore, that dominant strategy equilibrium, although easy to arrive at, does not happen always. For it demands too much. It demands that a particular strategy of A (or B) be optimal for all choices of B’s strategy (or A’s strategy).

However, instead of demanding so much, we may just require that A’s choice be optimal for the (optimal) choices of B. Of course, what is optimal for B will depend again on A’s choice. And so, we come to the concept of what is known as the Nash equilibrium.

We will say that a pair of strategies form a Nash equilibrium (named after an American mathematician John Nash) if A’s choice is optimal, given B’s choice, and B’s choice is optimal given A’s choice, [Let US remember that player A (or B) does not know what player B (or A) will do when he has to make his own choice of strategy. But each person may have some expectations about what the other person’s choice will be. As such, a Nash equilibrium can be expected as a pair of expectations about each person’s choice such that neither individual wants to change his behaviour when the other person’s choice is revealed.]

In the case of Table 14.2, the combination of strategy 1 of A and strategy 1 of B is a Nash equilibrium. To prove this, let us note that if A chooses his strategy 1, then the best thing for B to do is to choose also his strategy 1, for then his payoff would be 1, whereas from strategy 2, his payoff would be 0.

Again, if B chooses his strategy 1, then the best thing for A to do is to choose his strategy 1, for then his payoff would be 2, whereas from strategy 2 his payoff would be 0.

That is, here we have ob­tained that if A chooses his strategy 1, the optimal choice for B would be to choose strategy 1, and if B chooses strat­egy 1, then the optimal choice for A would be to choose his strategy 1. So, here, we have a Nash equilibrium. Each person is making the optimal choice given the other person’s choice.

It is obvious from the definition of Nash equilibrium that the Cournot equilibrium under oligopoly is a particular case of Nash equilibrium. In the Cournot equilibrium, the choices are of the output levels of the two duopoly firms.

Each firm chooses its output level taking the other firm’s choice as being fixed. Here the choice of the output level of each firm is the choice of its strategy and the amount of profit obtained by each firm is its payoff. In the Cournot model, each firm is supposed to do the best for itself, assuming that the other firm would continue to produce the output level, i.e., would continue to play the strategy, it had chosen for itself.

A Cournot equilibrium is obtained when each firm is maximising profits given the other firm’s behaviour. This is precisely the definition of Nash equilibrium.

However, the Nash equilibrium has its problems too. First, a game may have more than one Nash equilibrium. For example, in Table 14.2, the combination of strategy 2 of player A and strategy 2 of player B also gives us a Nash equilibrium. We may verify this by the kind of argument given above, or, we may just note that the structure of the game is symmetric.

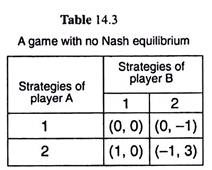
The second problem with the concept of a Nash equilibrium is that there are games that have no Nash equilibrium at all of the sort we have been describing. For example, let us consider the game given in Table 14.3. Here the Nash equilibrium does not exist.

For here, if player A plays his strategy 1, then player B will also play his strategy 1. But if player B plays strategy 1, player A will want to play strategy 2 (not strategy 1). Again, if player A plays strategy 2, player B will want to play his strategy 2 (not strategy 1). But if player B plays strategy 2, player A will decide to play strategy 1 (not strategy 2). Therefore, here Nash equilibrium never occurs.

Mixed Strategies:

So far we have been assuming that each player is choosing a strategy once and for all. That is, each player sticks to the choice of strategy once made. This is called a pure strategy.

However, alternatively, we may allow the players to play their choice at random according to some assigned probabilities. For example, we might assume that player A plays his strategy 1, 50 per cent of the time, and strategy 2,50 per cent of the time, while B plays his strategy 1,50 per cent of the time and strategy 2,50 per cent of the time. This kind of strategy is called a mixed strategy.

If A and B follow the mixed strategies given above of playing each of their choices half the time, then we have:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

The Prisoner’s Dilemma:

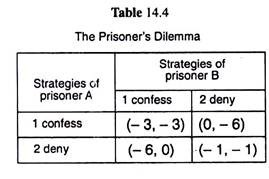
One problem with the Nash equilibrium of a game is that it does not necessarily lead to Pareto- efficient outcomes. Let us consider, for example, the game given in Table 14.4. This game is known as the prisoner’s dilemma.

In this game, we consider a situation where two prisoners who were partners in a crime were being questioned separately. Each prisoner had two op­tions—that of confessing to the crime, and thereby implicating the other, or, that of denying that he had any role in the crime.

The payoff aspects of the game are: If only one prisoner confessed, then he would go free, and the other prisoner would be booked and sent to prison for 6 months. If both prisoners denied having any role in the crime, then both would be held for 1 month on a technical ground, and if both pris­oners confessed, they would both be held for 3 months.

For the sake of simplicity, the payoffs are quantified by putting a negative sign before the various prison terms mentioned above, and accordingly, the payoff matrix is given in Table 14.4.

An examination of this matrix gives us: If prisoner B uses his strategy 2 (deny), then the prisoner A would certainly be better off if he uses his strategy 1 (confess), for then he would be set free.

Similarly, if prisoner B uses strategy 1 (confess), then prisoner A would be better off if he also uses his strategy 1 (confess), because if he does otherwise, i.e., uses his strategy 2 (deny), then he would get a sentence of 6 months. Thus, whatever the prisoner B does, prisoner A is better off if he uses his strategy 1 (confess).

The same thing is obtained for prisoner B also, i.e., he is better off using his strategy 1 (con­fess) whatever prisoner A does. Thus, in this game, the unique Nash equilibrium would occur when both prisoners decide to use their strategy 1, i.e., when both decide to confess, because if prisoner A chooses strategy 1, then B would optimize by choosing his strategy 1, and if prisoner B chooses his strategy 1, then A would optimize by using his strategy 1.

It may be noticed also that equilibrium in Table 14.4 is not only a Nash equilibrium, but it is also a dominant strategy equilib­rium. For, here, for each prisoner, his strategy 1 (confess) is a dominant strategy.

However, we have noted at the very outset of this section that the Nash equilibrium solution may not necessarily be Pareto-efficient. For example, in the game given in Table 14.4, the Nash equilibrium combination (confess, confess) of the two prisoners is Pareto-inefficient, for if they adopt their respective second strategies, i.e., if they choose the combination (deny, deny), then both of them would have larger payoffs. The payoff combination now would be (-1, -1) whereas the Nash equilibrium payoff combination has been (-3, -3).

Prisoner’s Dilemma and Cartel Instability:

The prisoner’s dilemma may be used to illustrate a wide range of economic phenomena. One such field is cartel instability. If the members of a cartel stick to their respective quotas, then there is no danger to cartel stability. But if one or both of them produce more than the allotted quota of output, then the cartel faces grave instability, and it breaks down.

We may illustrate cartel instability if, in the game of prisoner’s dilemma, we replace the strategies of “confess” and “deny”, respectively, by “produce more than the quota” and “stick to the original quota” and assume the respective payoff combinations to be those given in Table 4.5.

Like the prisoner’s dilemma illustrated in Table 14.4, Table 14.5 illustrates the dilemma of the two member-firms of the cartel. Here each duopolist has two strategies, viz., produce more than the allotted quota and stick to the allotted quota.

Here the payoffs of different strategy combinations are—If both the duopolists stick to the original quota, i.e., if they abide by the agreement, then each would have a payoff of 15 [payoff combination in row 2, column 2], On the other hand, if both of them produce more then each would have a smaller payoff (here 10).

For example, if they shift from the cartel equilibrium to Cournot equilibrium, then both of them would have an equal but smaller payoff [payoff combination in row 1, column 1].

On the other hand, if one of the duopolists stick to the quota but the other duopolist produces more then the latter would be rewarded handsomely but the former would be at a disadvantage [payoff combination in row 1, column 2 or row 2, column 1].

That is, here the cartel instability arises from the dilemma that if a member of the cartel thinks that the other member will stick to his quota, then it will pay him to produce more than his own quota. But if he thinks that the other firm will overproduce, then he too might do it as well.

Let us now see what is the correct way to play the game in prisoner’s dilemma. If the game is not a repeated one, if it is a one-shot game, then the strategy of confessing or defecting from the cartel seems to be reasonable, for whatever the other player does, the confessing or the defecting player is better off, especially when he has no way of influencing the other person’s behaviour.