Median is a value which divides the series into two equal parts.
It is position which is exactly in the centre, equal number of terms lie on either side of it, when terms are arranged in ascending or descending order.
Definition:
“The median is that value of the variable which divides the group into two equal parts, one part comprising all values greater and the other all values less than median”.
“Median of a series is the value of the item actual or estimated when a series is arranged in order of magnitude which divides the distribution into two parts.” —Horace Secrist
Calculation of Median:
ADVERTISEMENTS:
A. Individual Series:
To find the value of Median, in this case, the terms are arranged in ascending or descending order first; and then the middle term taken is called Median.
Two cases arise in individual type of series:
(a) When number of terms is odd:
ADVERTISEMENTS:
The terms are arranged in ascending or descending order and then are taken as Median.
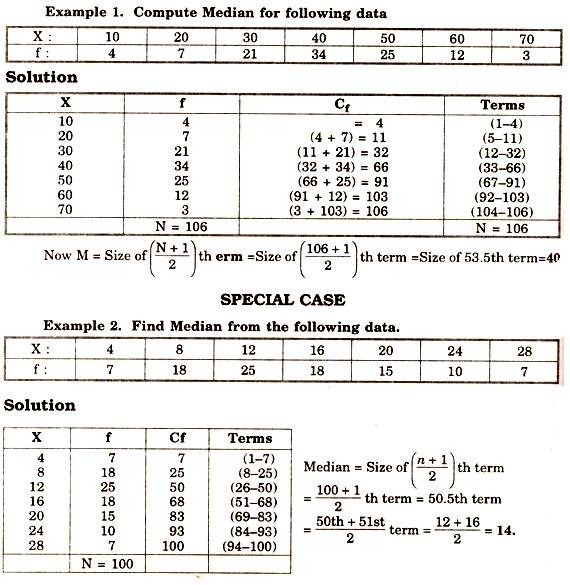
Example 1. Find Median from following data:
N = Total number of terms = 9
ADVERTISEMENTS:
Now = N+1/2 = 9+1 /2 = 2
Median = 5th term = 19.
(b) When number of terms is even:
In this case also, the terms are arranged in, order and then mean of two middle terms is taken as Median.
Example 2. From the following figures of ages of some students, calculate the median age:
Other Positional Measures (Quartile):
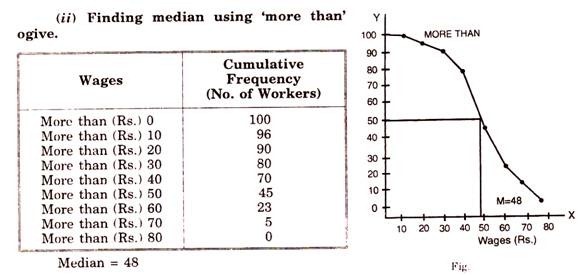
Positional Measures are also known as Partition Values. Median is also such value which divides the given series in two equal parts. Similarly Quartiles divide the series in four equal parts. Deciles in ten equal parts and percentiles in 100 equal parts. These measures are known as Depending Measures on Median.
Quartiles:
ADVERTISEMENTS:
Quartiles divide a series in four equal parts. For any series, there are three quartiles.
First or Lower Quartile:
Q1 divides the distribution in such a way that one-fourth (25%) of the total terms lie below it, and three-fourth lie above it.
ADVERTISEMENTS:
Method of Calculation:
Method to calculate any Quartile, Decile or Percentile is the same as that of Median; But only difference that is there, belongs to the divisor. To find the required value, in Median, the divisor is 2 as median divides the distribution in two equal parts. Thus the divisor is 10 and 100 in case of Deciles and Percentiles as they divide the distribution in 10 and 100 equal parts respectively.
Similarly the divisor is 4 in case of Quartiles; and in all these cases we multiply such result by a digit; whose value we have to find according to the given problem, which will be demonstrated in the coming formulae and examples.
ADVERTISEMENTS:
Individual Series:
We arrange the terms in ascending order and then take the total number of terms as N. Then we find the desired result from it as was in the case of Median.
Steps to Calculate:
1. Arrange the terms in ascending order.
2. Take total number of terms = N.
3. Then
ADVERTISEMENTS:
In case of decile n = 1, 2, 3— 9; and in case of percentile n = 1, 2, 3, -— 99.
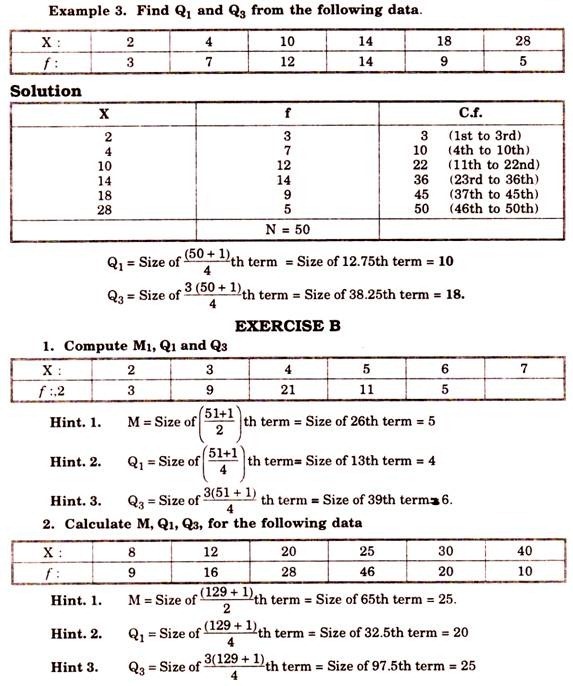
Example 1. Determine median Q1, Q3, from the following:
Marks in Statistics: 31, 29, 27, 33, 35, 41, 39, 41, 43, 45, 47.
Solution:
Here in this case we can’t stand in favour of Mean, because only one or two extreme values can affect the balance. Here we go in favour of Median as it is the positional measure, and is the middle value., Thus 1st preference is Make I and last preference is make (IV) But Make II and III have equal median and hence here use of Mean will be made and Make III is preferred to Make II. Therefore final order of preference will be Make I, Make III, Make II, Make (IV).
ADVERTISEMENTS:
(B) Discrete Series:
Here also the data is arranged in ascending or descending order; And the (N+1/2) term is taken after finding cumulative frequencies. Value of variable corresponding to that term is the value of Median.
Calculation of Median in Discrete Series:
After arranging the terms, taking cumulative frequencies, we take (N+1/2) and then calculate.
Steps to Calculate:
(1) Arrange the data in ascending or descending order.
ADVERTISEMENTS:
(2) Find cumulative frequencies.
(3) Find the value of the middle item by using the formula
Median = Size of (N+1/2)th item
(4) Find that total in the cumulative frequency column which is equal (N + 1/2)th or nearer to that value.
(5) Locate the value of the variable corresponding to that cumulative frequency This is the value of Median.
Other Positional Measures (Quartiles):
ADVERTISEMENTS:
A. Individual and Discrete Series:
We arrange the terms in ascending order and then take the total number of terms as N. Then we find the desired result from it as was in the case of Median.
Continuous Series:
In this case cumulative frequencies is taken and then the value from the class-interval in which (N/2)th term lies is taken. Using the formula.
M= L+ N1-Cf/f × i
Where N1 = N/2, L is lower limit of class interval in which frequency lies.
Cf is the cumulative frequency, f the frequency of that interval and i is the length of class interval.
Median can also be calculated from formula given below:
M= L – Cf-N1/f × i: Where L is upper limit of median class.
Important Working Hints:
1. Take N1=N/2
2. Looking from the lowest to upper side in the Cf column we get the value which is firstly numerically less than N1. It is value of Cf.
3. We come one step down; make the terms in column ‘f and also the class interval to get f and L. L is taken from lower limit of class interval.
Note:
We often use first formula; although second formula has also been applied in the example given below:
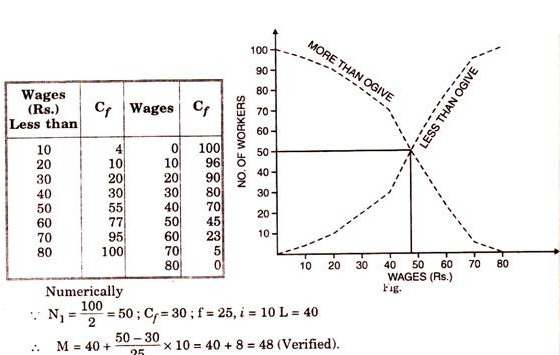
(ii) Finding median using both o gives simultaneously:
In this method, both o gives are drawn on the graph simultaneously corresponding values are derived by drawing perpendicular on y and x axes, from the poi where both curves cut each other as shown under-
Calculation of Median using “Less than and More than” o gives at a time