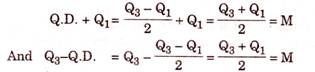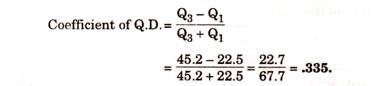How to Calculate Inter-Quartile Range? – Explained!

A. Quartile Deviation:

In range we calculate by L-S terms. But in this case we leave the first 25% and last 25% terms to avoid the undue importance of extreme values.

So it means that we get Q₁ and Q₃, if we leave first and last 25% terms.

Thus,

B. Inter-Quartile Range = Q₃ – Q₁

And; Semi Inter Quartile Range = Q₃ – Q₁ Q.D. Also

It is an absolute measure and is known as Quartile Deviation. (Q.D.).

Now as Median is the middle value, Q₃ is bigger than Median and median is bigger than Q₁, as Q₁, Q₂ = M and Q₃ cover 25, 50 and 75% of the terms.

The quartile deviation gives the average amount by which two quartiles differ from median. For a symmetrical distribution,

Q₃-M = M-Q₁; Where M = Median, Q₁ = Lower Quartile and Q₃ = Upper Quartile.

It means median lies half way on the scale from Q₁ to Q₃.

Thus for symmetrical distribution we have

Alternatively, for a symmetrical distribution,

Q₁₌M-QD and Q₃=M+QD

Coefficient of Quartile Deviation:

Quartile Deviation is an absolute measure of dispersion. Its relative measure is the coefficient of Quartile Deviation.

(B) Discrete Series: