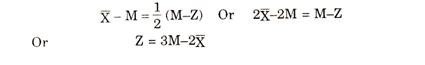Mode is the most popular term of the series and can be located easily. But its drawbacks or demerits are too big to discard it. It cannot be further treated algebraically also.
Median has also the same drawback that it cannot be treated further algebraically; and like mode, value of the whole sum of series cannot be found from its values and number of terms. It is also not so rigidly defined as is Mean.
Mean is the best measure of central tendency of the three. It is most rigidly defined, and is further capable of Algebraic Treatment. The sum of whole series can be found from its value and number of terms.
Thus going through the pros and cons of all these three, we find that mean has certain merits over the other two measures but it does not lower the merits of the other two. Although mean is most popular and important average but still there are fields where Median and Mode are best suited for Uni-modal Frequency Distribution
A. This formula was expressed by Karl Pearson as follows:
For moderately skewed distribution, the empirical relationship between Mean, Mode and Median can be expressed by the above formula.
This relationship is based on the fact that the distance between mean and median is half of the distance between mode and median, i.e.