Property I. Indifference curves slope downward to the right:
This property implies that an indifference curve has a negative slope.
This property follows from assumption I. Indifference curve being downward sloping means that when the amount of one good in the combination is increased, the amount of the other good is reduced. This must be so if the level of satisfaction is to remain the same on an indifference curve.
If, for instance, the amount of good X is increased in the combination, while the amount of good Y remains unchanged, the new combination will be preferable to the original one and the two combinations will not therefore lie on the same indifference curve provided more of a commodity gives more satisfaction.
ADVERTISEMENTS:
Property II: Indifference curves are convex to the origin:
Another important property of indifference curves is that they are usually convex to the origin. In other words, the indifference curve is relatively flatter in its right-hand portion and relatively steeper in its left-hand portion. This property of indifference curves follows from assumption 3, which is that the marginal rate of substitution of X for Y (MRSxy) diminishes as more and more of X is substituted for Y.
Only a convex indifference curve can mean a diminishing marginal rate of substitution of X for K If indifference curve was concave to the origin it would imply that the marginal rate of substitution of X for y increased as more and more of X was substituted, for Y.
When the indifference curve is convex to the origin, MRS diminishes as more of X is substituted for K. We therefore conclude that indifference curves are generally convex to the origin. Our assumption regarding diminishing MRSxy and the convexity of indifference curves is based upon the observation of actual behaviour of the normal consumer. If indifference curves were concave or straight lines, the consumer would succumb to monomania, that is, he would buy and consume only one good. We know that consumers in actual world do not generally buy and consume one good. It is for this reason that we reject indifference curves of concave or straight-line shapes and assume that indifference curves are normally convex to the origin.
ADVERTISEMENTS:
The degree of convexity of an indifference curve depends on the rate of fall in the marginal rate of substitution of X for Y. As stated above, when two goods are perfect substitutes of each other, the indifference curve is a straight line on which marginal rate of substitution remains constant. The better substitutes the two goods are for each other, the closer the indifference curve approaches to the straight line so that when the two goods are perfect substitutes the indifference curve is a straight line.
Property III: Indifference curves cannot intersect each other:
Third important property of indifference curves is that they cannot intersect each other In other words only one indifference curve will pass through a point in the indifference map 1 his property can be easily proved by first making the two indifference curves cut each other and then showing the absurdity or self-contradictory result it leads to.
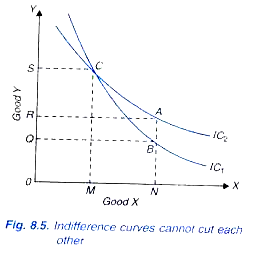
In Fig. 8.5 two indifference curves are shown cutting each other at point C. Now take point on indifference curve IC2 and point B on indifference curve IC1 vertically below A. Since an indifference curve represents those combinations of two commodities which give equal satisfaction to the consumer the combinations represented by points A and C will give equal satisfaction to the consumer because both lie on the same indifference curve IC2.
Likewise, the combinations B and C will give equal satisfaction to the consumer; both being on the same indifference curve IC1. If combination A is equal to combination C in terms of satisfaction, and combination B is equal to combination C, it follows that the combination A will be equivalent to B in terms of satisfaction. But a glance at Fig.8.5 will show that this is absurd conclusion since combination A contains more of good Y than combination B, while the amount of good X is the same in both the combinations.
Thus, the consumer will definitely prefer A to B, that is, A will give more satisfaction to the consumer than B. But the two indifference curves cutting each other lead us to an absurd conclusion of A being equal to Bin terms of satisfaction. We therefore conclude that indifference curves cannot cut each other.
Another point which is worth mentioning in this regard is that indifference curves cannot even meet or touch each other or be tangent to each other at a point. The meeting of two indifference curves at a point will also lead us to an absurd conclusion. The same argument holds good in this case as developed above in the case of intersection of indifference curves.
Property IV: A higher indifference curve represents a higher level of satisfaction than a lower indifference curve:
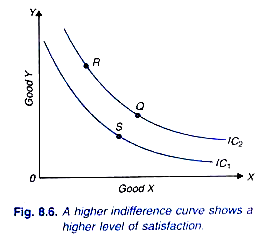
The last property of indifference curve is that a higher indifference curve will represent a higher level of satisfaction than a lower indifference curve. In other words, the combinations which lie on a higher indifference curve will be preferred to the combinations which lie on a lower indifference curve. Consider indifference curves IC1 and IC2 in Fig. 8.6. IC2 is a higher indifference curve than IC1. Combination Q has been taken on a higher indifference curve IC2 and combination S on a lower indifference curve IC1.
Combination Q on the higher indifference curve IC2 will give a consumer more satisfaction than combination S on the lower indifference curves IC1 because the combination Q contains more of both goods X and Y than the combination S. Hence the consumer must prefer Q to S. And by transitivity assumption, he will prefer any other combination such as combination R on IC2 (all of which are indifferent with Q) to any combination on IC1 (all of which are indifferent with S) We, therefore, conclude that a higher indifference curve represents a higher level of satisfaction and combinations on it will be preferred to the combinations on a lower indifference curve.
Indifference Curves of Perfect Substitutes and Perfect Complements:
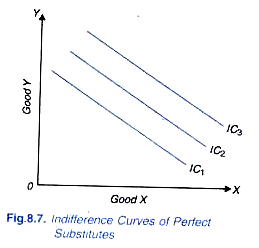
The degree of convexity of an indifference curve depends upon the rate of fall in the marginal rate of substitution of X for Y. As stated above, when two goods are perfect substitutes of each other, the indifference curve is a straight line on which marginal rate of substitution remains constant. Straight-line indifference curves of perfect substitutes are shown m Fig. 8.7.
The better substitutes the two goods are for each other, the closer the indifference curve approaches to the straight-line so that when the two goods are perfect substitutes, the indifference curve is a straight line. In case of perfect substitutes, the indifference curves are parallel straight lines because the consumer equally prefers the two goods and is willing to exchange one good for the other at a constant rate.
ADVERTISEMENTS:
As one moves along a straight-line indifference curve of perfect substitutes, marginal rate of substitution of one good for another remains constant. Examples of goods that are perfect substitutes are not difficult to find in the real world. For example, Dalda and Rath Vanaspati, two different brands of cold drink such as Pepsi Cola and Coca Cola are generally considered to be perfect substitutes of each other.
The greater the fall in marginal rate of substitution, the greater the convexity of the indifference curve. The less the ease with which two goods can be substituted for each other, the greater will be the fall in the marginal rate of substitution.
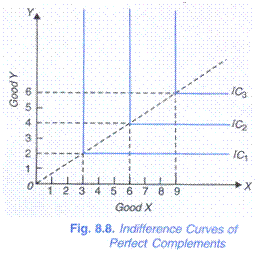
At the extreme, when two goods cannot at all be substituted for each other, that is, when the two goods are perfect complementary goods, as for example gasoline and coolant in a car, the indifference curve will consist of two straight lines with a right angle bent which is convex to the origin as shown in Fig. 8.8. Perfect complementary goods are used in a certain fixed ratio.
ADVERTISEMENTS:
As will be seen in Fig. 8.8 the left- hand portion of an indifference curve of the perfect complementary goods is a vertical straight line which indicates that an infinite amount of Y is necessary to substitute one unit of X and the right-hand portion of the indifference curve is a horizontal straight line which means’ that an infinite amount of X is necessary to substitute one unit of Y.
All this means that the two perfect complements are used in a certain fixed ratio and cannot be substituted for each other In Fig. 8.8 two perfect complements are consumed in the ratio, 3X: 27. Complements are thus those goods which are used jointly in consumption so that their consumption increases or decreases simultaneously. Pen and ink, right shoe and left shoe, automobile and petrol sauce and hamburger, type writer and typists are some examples of perfect complements.