Let us learn about the movement along the supply curve and shifts of the supply curve.
The supply curve of a commodity normally shows the relation between the quantities supplied of a commodity and its market price, assuming that all other factors influencing supply remain constant. On the basis of this assumption, we consider movements along the same supply curve from left to the right (or from right to the left).
But, in practice, we observe that other factors do not remain constant over time. If there is a change in another variable the whole supply curve will shift to a new position. So economists find it necessary to draw a distinction between a movement along the supply curve and a shift of the entire curve.
A movement along the same curve implies that a larger (smaller) quantity of a commodity is being supplied at a lower (higher) price. Such movements imply that different quantities are being offered for sale at different prices, ceteris paribus.
ADVERTISEMENTS:
Thus, if all the determinants of supply, except the own price of the commodity, remain constant then we have a change in quantity supplied. This is also called movement along the same supply curve caused by a change in the product’s own price.
Symbolically,
Sx = f(Px, P̅a… P̅c, P̅L… Po, T̅.C̅r, S̅t, O̅.G̅)
The bar signs over the heads of all the variables except Px indicates that those variables are constant.
ADVERTISEMENTS:
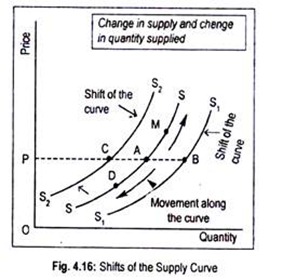
A movement along a supply curve occurs when a change in own price of a commodity causes a change in the quantity supplied. This may be explained in terms of Fig. 4.16. At the price OP, let PA be the supply of a commodity. If price rises, quantity supplied will increase to M and, if price falls, quantity supplied will decrease to D, along the supply curve SS. Thus, the term quantity supplied refers to a point on the supply curve.
On the other hand, there occurs a shift in supply when any of the determinants of supply, except the own price, changes. This means that the supply curve shifts bodily due to a change in something other than the product price. Symbolically,
Sx = f (P̅x, Pa…Pc,PL…P0,T, Cr, St, O,G)
ADVERTISEMENTS:
Here Px is fixed.
A shift of the supply curve implies that a different quantity is being offered for sale at a particular given price, as Fig. 4.16 shows. As the supply curve shifts from SS to S1S1 the quantity offered for sale at price OP goes up from PA to PB. Such shifts occur due to changes in one or more of the ceteris paribus assumptions and are known as changes in the conditions of supply.
If one of the determinants of supply— except own price—change, supply curve may shift backward or forward. At a price OP, quantity supplied is PA.
Now if taxes are imposed on the article, supply curve will shift from SS to S2S2, thereby reducing supply from PA to PC, even price of the good in question is kept at OP. On the other hand, assume that the price of raw materials declines. This causes SS curve to shift to the rightward direction to S1S1 and the supplier now supplies PB—a larger quantity than PA.
Table 4.5 summarizes the main causes of such shifts and indicates their direction.