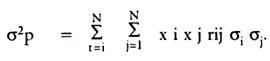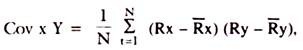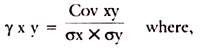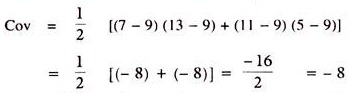In this article we will discuss about:- 1. Introduction to Markowitz Theory 2. Assumptions of Markowitz Theory 3. Diversification 4. Criteria of Dominance 5. Measurement of Risk.
Contents:
- Introduction to Markowitz Theory
- Assumptions of Markowitz Theory
- Diversification of Markowitz Theory
- Criteria of Dominance
- Measurement of Risk
1. Introduction to Markowitz Theory:
Harry M. Markowitz is credited with introducing new concepts of risk measurement and their application to the selection of portfolios. He started with the idea of risk aversion of average investors and their desire to maximise the expected return with the least risk.
ADVERTISEMENTS:
Markowitz model is thus a theoretical framework for analysis of risk and return and their inter-relationships. He used the statistical analysis for measurement of risk and mathematical programming for selection of assets in a portfolio in an efficient manner. His framework led to the concept of efficient portfolios. An efficient portfolio is expected to yield the highest return for a given level of risk or lowest risk for a given level of return.
Markowitz generated a number of portfolios within a given amount of money or wealth and given preferences of investors for risk and return. Individuals vary widely in their risk tolerance and asset preferences. Their means, expenditures and investment requirements vary from individual to individual. Given the preferences, the portfolio selection is not a simple choice of any one security or securities, but a right combination of securities.
Markowitz emphasized that quality of a portfolio will be different from the quality of individual assets within it. Thus, the combined risk of two assets taken separately is not the same risk of two assets together. Thus, two securities of TISCO do not have the same risk as one security of TISCO and one of Reliance.
Risk and Reward are two aspects of investment considered by investors. The expected return may vary depending on the assumptions. Risk index is measured by the variance of the distribution around the mean, its range etc., which are in statistical terms called variance and covariance. The qualification of risk and the need for optimisation of return with lowest risk are the contributions of Markowitz. This led to what is called the Modern Portfolio Theory, which emphasizes the tradeoff between risk and return. If the investor wants a higher return, he has to take higher risk. But he prefers a high return but a low risk and hence the problem of a tradeoff.
ADVERTISEMENTS:
A portfolio of assets involves the selection of securities. A combination of assets or securities is called a portfolio. Each individual investor puts his wealth in a combination of assets depending on his wealth, income and his preferences. The traditional theory of portfolio postulates that selection of assets should be based on lowest risk, as measured by its standard deviation from the mean of expected returns. The greater the variability of returns, the greater is the risk.
Thus, the investor chooses assets with the lowest variability of returns. Taking the return as the appreciation in the share price, if TELCO shares price varies from Rs. 338 to Rs. 580 (with variability of 72%) and Colgate from Rs. 218 to Rs. 315 (with a variability of 44%) during 1998, the investor chooses the Colgate as a less risky share.
As against this Traditional Theory that standard deviation measures the variability of return and risk is indicated by the variability, and that the choice depends on the securities with lower variability, the modern Portfolio Theory emphasizes the need for maximization of returns through a combination of securities, whose total variability is lower.
The risk of each security is different from that of others and by a proper combination of securities, called diversification one can arrive at a combination wherein the risk of one is offset partly or fully by that of the other. In other words, the variability of each security and covariance for their returns reflected through their inter-relationships should be taken into account.
ADVERTISEMENTS:
Thus, as per the Modern Portfolio Theory, expected returns, the variance of these returns and covariance of the returns of the securities within the portfolio are to be considered for the choice of a portfolio. A portfolio is said to be efficient, if it is expected to yield the highest return possible for the lowest risk or a given level of risk.
A set of efficient portfolios can be generated by using the above process of combining various securities whose combined risk is lowest for a given level of return for the same amount of investment, that the investor is capable of. The theory of Markowitz, as stated above is based on a number of assumptions.
2. Assumptions of Markowitz Theory:
The Portfolio Theory of Markowitz is based on the following assumptions:
(1) Investors are rational and behave in a manner as to maximise their utility with a given level of income or money.
(2) Investors have free access to fair and correct information on the returns and risk.
(3) The markets are efficient and absorb the information quickly and perfectly.
(4) Investors are risk averse and try to minimise the risk and maximise return.
(5) Investors base decisions on expected returns and variance or standard deviation of these returns from the mean.
ADVERTISEMENTS:
(6) Investors choose higher returns to lower returns for a given level of risk.
A portfolio of assets under the above assumptions is considered efficient if no other asset or portfolio of assets offers a higher expected return with the same or lower risk or lower risk with the same or higher expected return. Diversification of securities is one method by which the above objectives can be secured. The unsystematic and company related risk can be reduced by diversification into various securities and assets whose variability is different and offsetting or put in different words which are negatively correlated or not correlated at all.
Diversification of Markowitz Theory:
Markowitz postulated that diversification should not only aim at reducing the risk of a security by reducing its variability or standard deviation, but by reducing the covariance or interactive risk of two or more securities in a portfolio. As by combination of different securities, it is theoretically possible to have a range of risk varying from zero to infinity.
ADVERTISEMENTS:
Markowitz theory of portfolio diversification attaches importance to standard deviation, to reduce it to zero, if possible, covariance to have as much as possible negative interactive effect among the securities within the portfolio and coefficient of correlation to have – 1 (negative) so that the overall risk of the portfolio as a whole is nil or negligible.
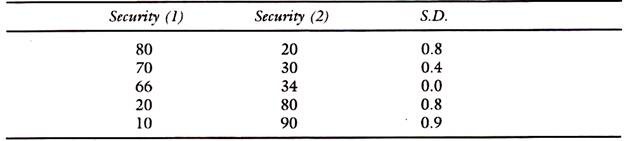
Then the securities have to be combined in a manner that standard deviation is zero, as shown in the example below:
Possible combinations of securities (1) and (2):
ADVERTISEMENTS:
In the example, if 2/3rds are invested in security (1) and 1/3rd in security (2), the coefficient of variation, namely = S.D./mean is the lowest.
The standard deviation of the portfolio determines the deviation of the returns and correlation coefficient of the proportion of securities in the portfolio, invested. The equation is-
σ2p = Portfolio variance
σp = Standard deviation of portfolio
xi = Proportion of portfolio invested in security i
ADVERTISEMENTS:
xj = Proportion of portfolio invested in security J
rij = Coefficient of correlation between i and J
σi standard deviation of i
σj standard deviation of J
N = number of securities
Problem:
ADVERTISEMENTS:
Given the following example, find out the expected risk of the portfolio.
Parameters of Markowitz Diversification:
Based on his research, Markowitz has set out guidelines for diversification on the basis of the attitude of investors towards risk and return and on a proper quantification of risk. The investments have different types of risk characteristics, some called systematic and market related risks and the other called unsystematic or company related risks. Markowitz diversification involves a proper number of securities, not too few or not too many which have no correlation or negative correlation. The proper choice of companies, securities, or assets whose return are not correlated and whose risks are mutually offsetting to reduce the overall risk.
For building up the efficient set of portfolio, as laid down by Markowitz, we need to look into these important parameters:
(1) Expected return.
ADVERTISEMENTS:
(2) Variability of returns as measured by standard deviation from the mean.
(3) Covariance or variance of one asset return to other asset returns.
In general the higher the expected return, the lower is the standard deviation or variance and lower is the correlation the better will be the security for investor choice. Whatever is the risk of the individual securities in isolation, the total risk of the portfolio of all securities may be lower, if the covariance of their returns is negative or negligible.
Criteria of Dominance:
Dominance refers to the superiority of one portfolio over the other. A set can dominate over the other, if with the same return, the risk is lower or with the same risk, the return is higher. Dominance principle involves the tradeoff between risk and return.
For two security portfolio, minimise the portfolio risk by the equation-
ADVERTISEMENTS:
σp = Wa σa2 + Wb σb2 + 2 (WaWbσaσb σab)
E (Rp) = WaE (Ra) + Wb E (Rb)
R refers to returns and E (Rp) is the expected returns, σp is the standard deviation, W refers to the proportion invested in each security σaσb are the standard deviation of a and b securities and σab is the covariance or interrelations of the security returns.
The above concepts are used in the calculation of expected returns, mean standard deviation as a measure of risk and covariance as a measure of inter-relations of one security return with another.
Measurement of Risk:
Risk is discussed here in terms of a portfolio of assets. Any investment risk is the variability of return on a stock, assets or a portfolio. It is measured by standard deviation of the return over the Mean for a number of observations.
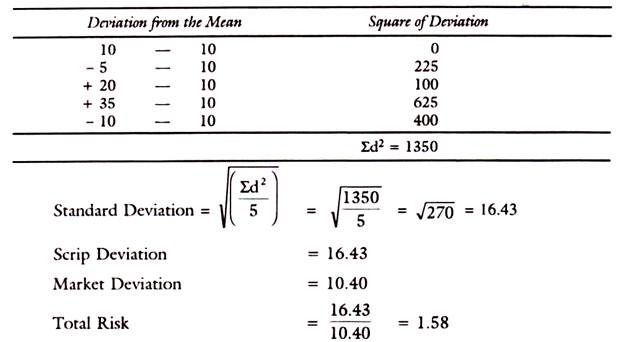
Example:
Standard deviation to be calculated: Average in Mean Observations: 10% – 5% 20% 35% – 10% = 10% will be their Mean.
Portfolio Risk:
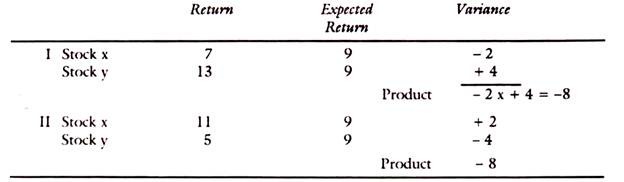
When two or more securities or assets are combined in a portfolio, their covariance or interactive risk is to be considered. Thus, if the returns on two assets move together, their covariance is positive and the risk is more on such portfolios. If on the other hand, the returns move independently or in opposite directions, the covariance is negative and the risk in total will be lower.
Mathematically, the covariance is defined as-
where Rx is return on security x, Ry return security Y, and R̅x and R̅y are expected returns on them respectively and N is the number of observations.
The coefficient of correlation is another measure designed to indicate the similarity or dissimilarity in the behaviour of two variables. We define the coefficient of correlation of x and y as-
Cov x y is the covariance between x and y and σx is the standard deviation of x and σy is the standard deviation of y.
Where, N = 2
The covariance equation is as follows:
The coefficient of correlation can be set out as follows:
If the coefficient of correlation between two securities is – 1.0, it is perfect negative correlation. If it is + 1.0 it is perfect positive correlation. If the coefficient is ‘0’ then the returns are said to be independent. To sum up, correlation between two securities depend- (a) on covariance between them, and (b) the standard deviation of each.
In Markowitz Model, we need to have the inputs of expected returns, risk measured by standard deviation of returns and the covariance between the returns on assets considered.