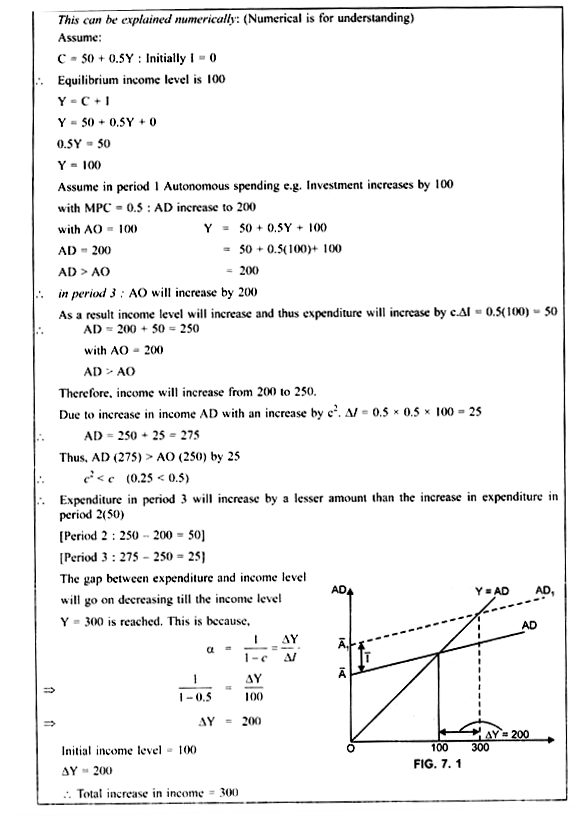
The Multiplier:
The concept of multiplier is derived from the concept of MPC.
It refers to effect of change in Autonomous spending on aggregate income through induced consumption expenditure.
It is the amount by which equilibrium output level changes when autonomous spending (A) changes by 1 unit. It is the ratio of change in equilibrium output level to a change in Autonomous Spending (A)
ADVERTISEMENTS:
α = ∆Y/∆A
Increase in autonomous spending (∆A) causes multiple increase in the equilibrium output and income level and the value of its multiple is given by multiplier. However, the value of multiplier depends on MPC. Greater the value of MPC, greater is the value of multiplier because a larger fraction of additional income will be consumed. This will lead to an increase in demand.
ADVERTISEMENTS:
The multiplier theory recognizes the fact that change in income due to change in investment is not instantaneous. It is a gradual process by which income changes. The process of change in income involves a time lag. Thus, the multiplier is a stage by stage computation of change in income resulting from a change in investment till the full effect of multiplier is not realized.
Thus, Induced expenditure in the third period will be less than the induced expenditure in the second period.
Greater the value of MPC, greater is the value of multiplier (α)
e.g. (i) MPC = 0.8
α = 1/1-0.8 = 5
(ii) If MPC = 0.6
α = 1/1-0.6 = 2.5
This is because high MPC implies that a greater fraction of additional increase in income will be consumed. Therefore, in every successive rounds (period), there will be greater increase in induced spending.
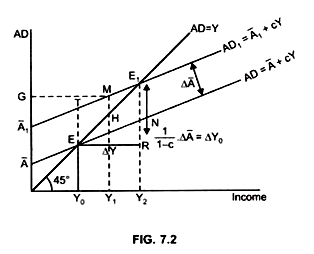
But at this output AD > AO by MH, that is, there will still exist a gap between AD and AO by MH.
ADVERTISEMENTS:
To build up this gap again production will increase. As a result, the gap between aggregate demand and output will decrease (MH < TE) because MPC < 1
This process will continue till a balance between AD and Aggregate output is not restored. This is at point E1