Irving Fisher analyzed the inflation-interest linkage.
The linkage shows that in the long run real interest rate is unaffected by monetary disturbance which affects the inflation rate.
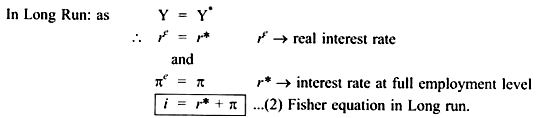
Fisher Equation shows that nominal interest rate can change when either expected real interest rate changes or when expected inflation rate changes.
Fisher equation shows that: in the short run during adjustment process any change in the real interest rate and expected inflation are reflected in the change in nominal interest rate. But, in the long-run economy returns to full employment level of output. The real rate of interest returns to its full employment level (r*) and π = πe
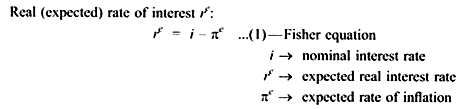
Equation 2 shows that in the long run, when all adjustments have occurred, an increase in inflation is fully reflected in nominal interest rates. Monetary policy becomes ineffective in changing the real interest rate.
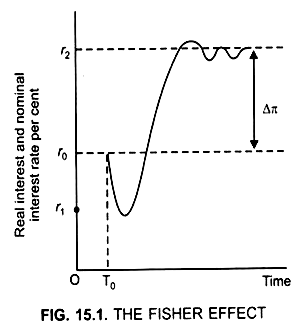
Depending on expectations, the nominal interest rate first falls and then rises. Fig, (15.1) e.g., If the nominal money supply increases by 3%.
There will be 3 phases of adjustment:
1. Liquidity effect: (It shows the impact of increased real balances on the interest rate)
ADVERTISEMENTS:
In time period T0, money supply is increased by 3%
Initial impact of increase in money supply is: Decrease in interest rate from r0 to r1 (Fig. 15.1)
2. Income effect:
ADVERTISEMENTS:
When nominal interest rate falls from r0 to r1 Investment will increase. This will lead to increase in AD (Reason: Y = C + I + G) with aggregate output (AO) constant, AD>AO
... Inventories will decrease.
Result:
production, that is, output will increase.
This in turn will lead to an increase in demand for labour. When demand for labour increases wages will increase and as a result price will increase. When price increases M/P, that is real money growth falls and as a result the interest rate rises to r2.
(c) When dL ↑→ wages ↑ → cost of production ↑ → Price level ↑ → M/P ↓ → interest rate ↑
3. Fisher effect or the expectations effect:
Thus, in the long run, 3 per cent increase in the rate of inflation will lead to 3% increase in the nominal interest rate. This one-to-one relation between inflation and nominal interest rate is called the Fisher Effect.
ADVERTISEMENTS:
r0r2 = ∆ m0 = ∆π
∆r = ∆m = ∆π
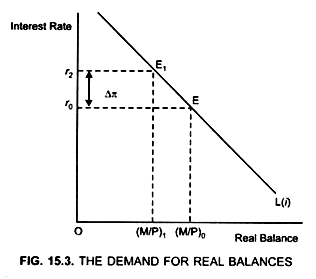
Figure (15.3) shows that increase in money supply and inflation will ultimately lead to a reduction in the real money stock, (M/P) from (M/P)0 to (M/P)1.
ADVERTISEMENTS:
As a result inflation and nominal interest rate increases from r0 to r2 in the long run.
Fisher effect:
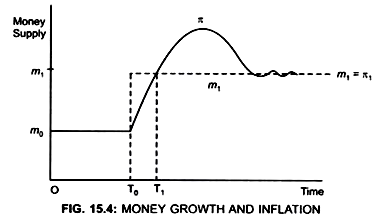
Figure (15.4) shows that:
ADVERTISEMENTS:
Initially at time period → T0
Money supply → m0
If in time period T0 money supply rises from m0 to m1.
Till time period T1 → Money supply > inflation rate and therefore real balances (M/P) will rise.
But after time period T1 Real balances fall because inflation rate > money growth.
This implies that in the long run real balances will be reduced.