Effects of Excise Taxes in a Competitive Industry | Microeconomics

In this article we will discuss about the effects of excise taxes in a competitive industry.

Excise taxes, also known as commodity taxes, are imposed on the production of commodities generally on a per unit basis. The tax is paid to the government by the producer rather than the buyer. (But this will not change in any way the effects of the tax if the collection costs are essentially the same for the producers and buyers.)

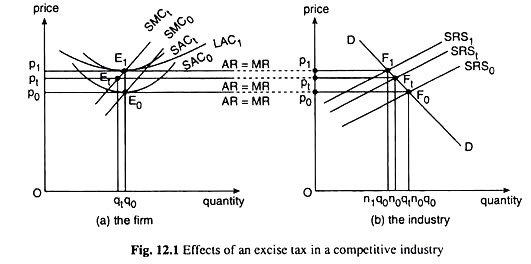
We shall also assume that technology or factor prices do not depend on total industry output. We shall try to know the effects of the tax, under perfect competition, on prices, industry output, firm output and the number of firms in the industry in the short run and in the long run. Part (a) of Fig. 12.1 illustrates the behaviour of a typical firm and part (b) illustrates the behaviour of the industry.

The Effects of the Tax in the Short Run:

To make our discussion easier we shall assume that all firms in the industry are identical and that the number of firms is n₀ before the tax is imposed. Part (a) of Fig. 12.1 shows the short-run average cost (SAC) curves and the associated marginal cost (SMC) curves of a typical firm.

The firm is in short-run and long-run equilibrium, earning only normal profit at the price p₀ and the output q₀. Part (b) of the figure shows the industry supply curves in the short run (the SRS curves) and the industry demand curve or the demand curve for the good (DD).

The short-run supply (SRS) curve of the industry is the horizontal summation of the SMC curves of the firms. It may be noted that the initial (short-run) equilibrium price of the good, p₀, has been determined at the point of intersection, F₀, of the supply and demand curves, SRS₀ and DD, of the industry.

We may remember here that, given the price, the profit maximising firm would produce the p = MC output. That is why the output q₀ of the firm has been determined at the point of intersection of the p = AR = MR and the SMC₀ curves. Since the number of firms is n₀ and the output of each firm is q₀, the short- run industry output is n₀q₀ at the point F₀.

Now, in Fig. 12.1 (a), when a per unit excise tax is imposed on the good, the average cost and the marginal cost of the good would increase at each output by the amount of the tax, say, t. Therefore, as the tax is imposed both the SAC and SMC curves of the firm would have vertical shifts by the amount of the tax. They would now become SAC_t and SMC_t in place of SAC₀ and SMC₀. Since SAC now is higher at each output by an equal amount which is the amount of the tax, the minimum SAC now would be obtained at the same output as before, i.e., at q = q₀.

That is, the minimum point of the SAC curve would move up vertically from E₀ on SAC₀ to E₁ on SAC_t, or, the pre-tax and post-tax minimum SAC would occur at the same output, viz., q₀ and the post-tax SMC curve, SMC_t, would pass through E₁. Since the post-tax SMC curve, SMC_t, lies to the left of SMC₀, the post-tax output of the firm would be smaller at each price than what it would have been initially.

In part (b) of Fig. 12.1, the short-run supply (SRS) curve of the industry would also have a vertical shift by the amount of the tax. Since the SMC curves of the firms would shift up vertically by the amount of the tax, the SRS curve of the industry, which is their horizontal summation, would also shift up vertically by the amount of the tax from SRS₀ to SRS_t.

We may think in another way also. Because of the imposition of the per unit tax, the supply price of each output of the firm and of the industry will increase by the amount of the tax. That is why the SRS curve of the industry will have a vertical shift by the amount of the tax.

Since there has been a shift in the supply curve of the industry from SRS₀ to SRS_t, demand curve remaining unchanged, the demand-supply equilibrium point would no longer remain the same—it would move from the point F₀ to the point F_t.

At the point F_t, the price of the good would increase from p₀ = OP₀ to p_t = OP_t, p_t – p₀ < t, i.e., because of the imposition of the tax, price has increased but by less than the amount of the tax. This is because of the following reasons.

The imposition of the per unit tax makes the supply price at each output higher by the amount of the tax. Therefore, if price increases by the amount of the tax, quantity supplied would remain the same, but unless the demand is perfectly inelastic, i.e., unless the demand curve is a vertical straight line, the quantity demanded would not remain unchanged, it would fall, and, so, the market can clear only at a price which is higher than the initial price but by less than the amount of the tax.

But, if the demand curve for the good is a vertical straight line, then only, as price increases by the amount of the tax, the quantity supplied, and also the quantity demanded, would remain unchanged, and the market would clear at the price which is higher than the initial price by the amount of the tax.

So in part (b) of Fig. 12.1, since the demand is not perfectly inelastic and the demand curve is not vertical, since it is negatively sloped, price would increase as a result of the imposition of the per unit tax, but by less than the amount of the tax.

In our case, price has increased from p₀ to p_t. Given this price, the firm in part (a) of Fig. 12.1 reduces its output from q₀ to q_t and the short-run industry output becomes n₀q_t at the point F_t.

Now the coordinates of the minimum point, E_t, of the SAC₁ curve are (q₀, p₀ + t) and those of point E_t are (q_t < q₀, p_t < p₀ + t). This means that, in the post-tax situation, p_t is below the minimum average cost, and the firms are suffering short-run economic losses. And so the industry would have to go through the process of long-run adjustments to arrive at a new long-run equilibrium.

Therefore, that the short-run effects of the tax will be to increase the price of the product, but by less than the amount of the tax, to decrease the output of each firm and to decrease the industry output, the number of firms remaining unchanged at n₀ in the short-run.

The Effects of the Tax in the Long Run:

The short-run losses caused by the tax forces some of the firms to leave the industry in the long run. Our comparative static analysis cannot tell us which firm leaves when but we can say that firms will be leaving the industry so long as losses persist.

Of course, the losses will not continue indefinitely. As the number of firms decreases in the long run, the short-run supply of the industry at each price will also decrease, and so, the SRS curve of the industry will be shifting leftward from SRS, as the exodus of firms continues. Demand conditions remaining the same, this will cause the price of the good to rise from p_t.

As the price of the good rises, the economic losses of the remaining firms tend to decrease. The process will continue till the number of firms has reduced to such a low and the price of the good has increased to such a high that the loss of the still remaining firms has reduced to zero, i.e., the firms happen to earn the normal profit.

At this point the exodus of firms stops, and the firms and the industry get back to a new post-tax long-run equilibrium at the point F₁.

Precisely, when the price of the product has risen from p, to p₀ + t = p₁, i.e., the price has risen by the amount of the tax over the initial pre-tax price, the firm’s AR = MR line touches the SAC, curve at its minimum point which is also the minimum point of its LAC curve, the firm again reaches a long-run equilibrium earning only the normal profit.

This price, p₁ is Obtained when the SRS curve has shifted leftward from SRS_t to SRS₁ as the number of firms has dwindled to, say, n) from n₀. The output of each firm at the new long run equilibrium point, E₁, is q₀ and the industry output would be n₁q₀ at the point F₁.

Therefore, that in the long run, after the imposition of the tax, the price of the product concerned increases by the amount of the tax, the quantity produced by each firm remains the same at the pre-tax level, the number of firms diminishes and the industry output also diminishes.

We may summarise the short-run and long-run effects of a per unit excise tax on a commodity by means of Table 12.1.