Can a Trade Union Raise Wage Rate and Employment?

Trade Union Powers to Secure Increases in Wage and Employment and to Eliminate Monopsonistic Exploitation of Labour:

The goals that the trade unions generally pursue are maximisation of employment, maximisation of total wage bill, and maximisation of total gains to the union as a whole. The trade unions may also try to achieve an increase in the wage rate accompanied by an increase in employ­ment.

The last goal, perhaps, is the most desirable for the unions. However, exactly what kind of gain the trade unions will be able to secure for their members would depend upon the organi­sation of the labour market.

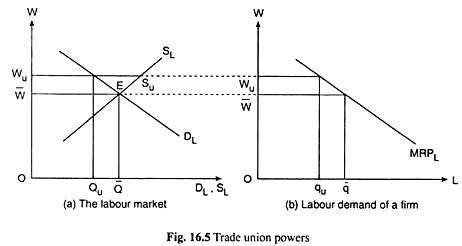
Let us consider a typical labour market with a negatively sloped labour demand curve, D_L, and a positively sloped labour supply curve, S_L, as given in Fig. 16.5(a).

If the workers in this market are unionized, and if the union dictates a wage rate, say, W_u, which is higher than the demand-supply equilibrium wage rate = W̅, then the union at the same time would be ready to supply any amount of labour at W = W_u, which is less than or equal to W_US_U, because the labour supply curve indicates that a maximum of W_US_U of labour would be available at W = W_u. Also, to obtain a supply of labour greater than W_US_U, the rate of wage would have to go up accordingly along the S_L curve.

In other words, at the rate of wage, W_u, dictated by the union, the labour supply curve would be perfectly elastic, i.e., it would be a horizontal straight line for 0 < S_L < W_u S_u, and it would be the positively sloped curve S_L for S_L > W_US_U. That is, here the supply curve of labour would be a curve in two parts.

The first part of this curve would be a horizontal straight line like W_US_U in Fig. 16.5(a), then the curve would have a kink at the point S_u to become positively sloped like the segment S_US_L. Let us remember that the horizontal segment, viz., W_US_U, of the S_L curve here is the average expense for labour (AE_L) curve and, at the same time, it is the marginal expense for labour (ME_L) curve because of the average-marginal relation.

In order to know about the powers of the trade union, let us first suppose that the labour market is perfectly competitive, i.e., the number of buyers and sellers of labour is large and they are unorganised. The situation is shown in Fig. 16.5(a) where the D_L and S_L curves are the demand and supply curves for labour.

At the point of intersection, E, of these curves, the mar­ket equilibrium wage rate has been obtained to be W and the quantity demanded and supplied of labour has been obtained to be Q. In Fig. 16.5(b), the demand curve for labour of each individual firm is shown to be MRP_L. At W = W̅, each firm’s demand for labour is q̅.

Let us now suppose that the labour market is unionized and the union demands a rate of wage W = W_u > W̅. The supply curve of labour now becomes W_US_US_L with a kink at the point S_u, and the horizontal segment W_US_U is now an AE_L = ME_L segment.

Now, if the firms accept the demand of the union, the rate of wage would rise from W̅ to W_u, and the firms’ collective demand for labour would fall from Q̅ to Q_u. Each individual firm’s demand for labour would now fall from q̅ to q_u (units).

We have obtained, thus, that if the labour is unionized in an erstwhile competitive labour market, wages would increase with an accompanying decline in employment. Under the circumstances, we have the following to say about the benefits or otherwise that the trade union might achieve for the workers.

If the demand for labour is relatively inelastic (e < 1), then, as we know, the rise in W would be accompanied by a rise in the firm’s total expense for labour. In this case, although employ­ment has declined, the total wage bill of the workers will increase. If the union could somehow divide equitably the earnings of Q_u employed workers among the Q̅ potential workers, then all the Q̅ workers might benefit.

However, if the demand for labour is relatively elastic (e > 1), then a rise in W caused by the union will result in a fall in employment accompanied by a fall in the total wage bill. Therefore, now the union would not be able to compensate the W̅ – W_u workers who are unemployed because of the rise in W. Thus, in a perfectly competitive labour market, unionization of the workers is not an unmitigated blessing.

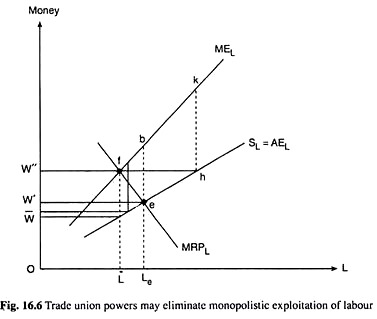
But in monopsonistic (or oligopolistic) labour markets, the trade unions would be able to benefit its members if they formulate rational policies. Let us consider a monopsonistic labour market as shown in Fig. 16.6 where the S_L (= AE_L) curve is the monopolist’s supply curve of labour or the average expense curve for labour, and the ME_L curve is the marginal to this curve, and also, the MRP_L curve is the firm’s marginal revenue product curve of labour.

Now if the labour force is not organised, i.e., if there is monopsony in the labour market and monopoly in the product market, the labour market equilibrium will occur at the point f which is the point of intersection of the MRP_L and ME_L curves.

At this point, the wage rate will be W̅ and the equilibrium quantity of labour demanded will be L. Here since W̅ < MRP_L, there would be full-length monopsonistic exploitation of labour of the total vertical gap between the ME_L and AE_L functions—this vertical gap, it may be remembered, is due to the existence of monopsony in the labour market.

Let us now suppose that the workers organise themselves in a union that would bargain collectively on their behalf with the monopsonist. We shall see now what may be the rational policies of the union to conduct collective bargaining. At one extreme, the union may want to achieve maximum employment for its members, whatever may be the wage obtained.

At the other extreme, the union may strive to maintain the present level of employment and secure the maximum possible amount of wage rise. Of course, in between these two extremes, the union may go in for a mixture of some rise in employment and some rise in wages that would best serve the interests of the workers.

If the union decides to pursue the policy for securing the maximum possible employment, then it would pick up the point of intersection, e, of the demand curve for labour, MRP_L, and the supply curve of labour S_L. At this point, the rate of wage that the union would have to set is W’. At W = W’, the post-union AE_L curve or supply curve of labour would be W’e S_L with a kink at the point e.

The corresponding ME_L curve would be a curve in two parts—one part is W’e that is the horizontal segment of the AE_L curve and another part is b ME_L; between these two parts there would be a vertical discontinuity. Here the point of intersection of the MRP_L and ME_L curves is the point e which, by definition, is the equilibrium point. At this point, the rate of wage is W’ and the amount of employment is L_e.

In this case, by setting W = W’, the union secures the maximum possible employment and also a wage rise, since W’ > W̅. The more important point to note here is that the labour now is getting a rate of wage (W’) which is equal to its MRP, i.e., the union power here has been able to completely eliminate the monop­sonistic exploitation of labour.

Next, if the union decides to maintain the initial level of employment L = L, then it would pick up the point f and set W = W”. Consequently, the S_L = AE_L curve here would be W”h S_L with a kink at the point h and the ME_L curve would be W”h k ME_L with a discontinuity at the point h over the vertical stretch hk. The firm’s equilibrium point, i.e., the MRP_L = ME_L point, now would be the point f.

At this point the amount of employment is L̅ which is the same as the initial level and the wage rate is W” which is greater than the initial rate, viz., W. Since W” – W̅ > W’ – W̅, here it has been possible for the union to secure a higher rise in W along with the initial level of employment than it secured a smaller rise in W, but, of course, some rise in employment also.

In the present case, the monopsonistic exploitation of labour has been completely eliminated, since W” = MRP_L at the point f.

We have discussed above the two extreme policies that the labour union can pursue when there is monopsony in the labour market. In both these cases, the monopsonistic exploitation is completely done away with, but the union has not been able to achieve an increase in W along with an increase in employment in both the cases.

In one case, there has been a rise in employment (in fact, maximum possible employment has been achieved) and a rela­tively smaller rise in W, but in the other case, the level of employment remaining the same, there has been a relatively larger rise in W.

However, we may also see with the help of Fig. 16.6 that if the union sets a W between W’ and W”, then it would be able to achieve an increase in both W and employment. In that case, the firm’s equilibrium point would be situated at some point on the segment of the MRP_L curve.

Since this segment is negatively sloped, the higher the rise in W, the lower would be the rise in employment that the union might secure for the workers. However, in all such cases, we would have W < MRP_L and there would happen some monopsonistic exploitation of labour.

We may also see in Fig. 16.6 that if the union sets W in between W’ and W̅, then the MRP_L function would pass through the vertical discontinuity of the ME_L curve. In all such cases, the firm cannot be in equilibrium at the MRP_L = ME_L point.

For the sake of profit maximisation, it would have to select the right extreme point of the horizontal segment of the ME_L function just before the discontinuity sets in. Therefore, in all such cases, the firm would be in equilibrium at an ME_L < MRP_L point, securing a rise in both W and employment. But in all such cases, we would have W = ME_L < MRP_L and so, monopsonistic exploitation cannot be eliminated.