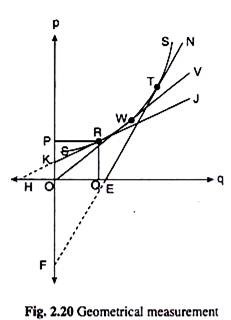
The geometric measurement of price-elasticity of supply can be obtained with the help of Fig. 2.20.
Suppose, the supply curve of a good is the curve SS which is given in this figure. Also suppose, intend to obtain the geometrical measure of the coefficient of price-elasticity of supply (ES) at the point R (OP, OQ) on the supply curve SS.
In order to obtain the slope of the supply curve at the point R, draw a tangent HRJ to this curve at R. The points of intersection of this tangent with the horizontal and vertical axis are H and K respectively.The slope of this tangent is equal to the slope of the supply curve, SS, at the point R.
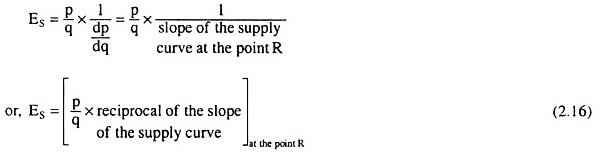
The value of ES can be easily obtained in terms of geometry. By virtue of the formula (2.16)
ADVERTISEMENTS:
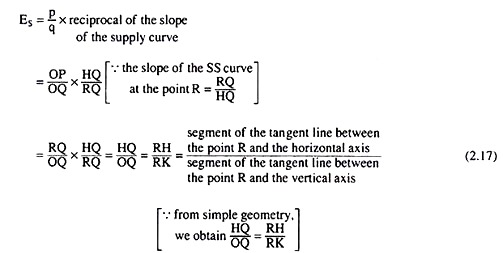
We have,
ADVERTISEMENTS:
ADVERTISEMENTS:
(2.17) helps to obtain the geometrical measurement of ES at any point R on the supply curve SS, draw a tangent to the supply curve at R, and ES then would be obtained as the ratio of the segment of the tangent line between the point R and the horizontal axis, and the segment of the tangent between the point R and the vertical axis.
Since, in Fig. 2.20, the tangent line HKRJ has intersected the vertical axis on the latter’s positive side, to get RH > RK. Therefore, in this case, ES > 1, i.e., here the supply of the good would be relatively elastic. Again, the tangent at the point, T, to the supply curve is FETN, and we would have ES= TE/TF (2.18) [by virtue of (2.17)]
ADVERTISEMENTS:
Since the tangent line FETN has intersected the horizontal axis on its positive side, TE < TF and Es < 1, i.e., here the supply of the good is relatively inelastic. Lastly, the tangent, OWV, to the supply curve at the point W, passes through the origin, and, at W, WO would have ES = WO/WO = 1 [by virtue of (2.17)]
i.e., here the supply of the good would be unitary elastic.
To obtain the geometrical measurement of price-elasticity of supply at any point on the supply curve, first, draw a tangent to the curve at the said point. Es then would be given by the ratio of the segment of the tangent line between the said point and the horizontal axis and that between the said point and the vertical axis.
If the tangent meets the vertical axis in its positive section, ES would be greater than one; if it meets the horizontal axis in its positive section, ES would be less than one; and if it meets the point of origin, Es would be equal to one. On the basis of this analysis, the price-elasticity of supply of a good would be different at different prices or at different points on its supply curve.