Consumer’s Equilibrium (With Diagram)

In this article we will discuss about the concept of consumer’s equilibrium, explained with the help of suitable diagrams and graphs.

A consumer is said to be in equilibrium when he feels that he “cannot change his condition either by earning more or by spending more or by changing the quantities of thing he buys”. A rational consumer will purchase a commodity up to the point where price of the commodity is equal to the marginal utility obtained from the thing.

If this condition is not fulfilled the consumer will either purchase more or less. If he purchases more, MU will go on falling and a situation will develop where price paid will exceed MU. In order to avoid negative utility, i.e., dissatisfaction, he will reduce consumption and MU will go on increasing till P = MU.

On the other hand, if MU is greater than the price paid, the consumer will enjoy surplus satisfaction from the units he has already consumed. This will induce him to buy more and more units of the commodity leading to successive fall in MU till it is equated to its price. Thus, by a process of trial and error — by buying more or less units, a consumer will ultimately settle at the point where P = MU. Here, his is total utility is maximum.

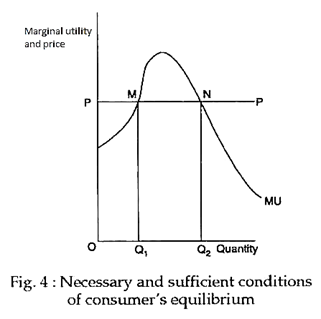
However, P = MU is a necessary but not a sufficient condition for a consumer’s equilibrium. In Fig. 4, we find that the MU curve is intersecting the price curve PP at two differ­ent points M and N. So far M is concerned, although by having OA quantity the consumer is reaching the point where P – MU but it is not equilibrium.

For by purchasing extra units above OA he can enjoy surplus satisfaction. Why then will he stop at OA? He will continue using the thing till he reaches OB. If he goes beyond this point, for every extra unit P is greater than MU and he shall have to suffer dissatisfaction. Thus, the sufficient condition of consumer equilibrium is that the MU curve must cut the price curve at its downward segment and not at its rising segment.

The objective of a rational consumer is to maximise utility (wel­fare) subject to:

(1) A fixed level of money income 

(2) A fixed set of commodity prices.

Now, what is fundamental equilibrium condition that has to be satisfied if a consumer is spending his income on different goods so as to make himself truly best off in terms of utility or satisfaction?

Certainly he would not expect that the last egg he is buying brings him exactly the same marginal utility as the last cake he is buying. One cake costs much more than an egg. One may guess that he should go on buying a good which costs twice as much per unit as another until he ends up in his equilibrium bringing him just twice as much in marginal utility.

Thus, if the consumer has arranged his consumption so that every single good brings him marginal utility just exactly proportional to its price, then he could not gain extra utility and thus improve his position by departing from such an equilibrium.

This fundamental condition can now be stated:

A consumer with a fixed money income and facing a fixed set of market prices of goods can reach equilibrium or the level of maximum satisfaction or utility only when he acts thus;

Law of equal marginal utilities per rupee:

Each good — such as egg — is demanded up to the point where the marginal utility per rupee spent on it is exactly the same as the marginal utility of a rupee spend on any other good—such as cake.

Why does this law hold? If any one good gave more marginal utility per rupee the consumer would gain by taking money away from other goods and spending more on that good — up to the point where the law of diminishing marginal utility brought its marginal utility per rupee down to equality. If any good gave less marginal utility per rupee than the common level, the consumer would buy less of it’s until the marginal utility of the last rupee spent on it had risen back to the common level.

The Law of Equi-marginal Utility (or the Principle of Substitution) fol­lows from the Law of Diminishing Marginal Utility. According to the latter, a person goes on buying the units of a commodity one after another till its marginal utility becomes equal to its price. In the case of more than one commodity, he examines the marginal utility of the last unit of money spent on the different commodities.

More precisely, for the maximisation of satisfaction, income must be allocated in such a way that the marginal utility of an unit of money’s worth (for example, one rupee’s worth) is the same for every commodity. If it is found that the marginal utility of the last unit of money spent on say, X commodity is greater than that derived from another commodity, say, Y commodity, he substitutes X for Y. Such a process of substitution goes on till the marginal utility of the last unit of money spent on X and on Y becomes equal to each other.

Beyond this point, further substitution will not be beneficial to him, for that would involve a decrease in his total utility. This is known as the Law of Equi-marginal Utility. Marshall puts the Law in the following words: “If a person has a thing which he can put to several uses, he will distribute it between these uses in such a way that it has the same marginal utility in all”. If he has a greater utility in one use than in another, he would gain by taking away some of it from the second use and applying it to the first.

Proof of the Law:

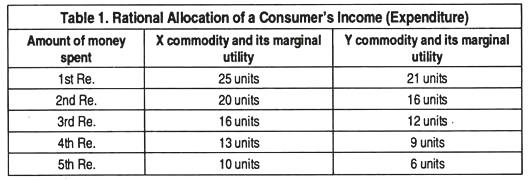
The Law of Equi-marginal Utility can be proved as follows- Let us suppose that a person has Rs. 5 to spend on X and Y commodities during a particular period of time, say a day, and he gets marginal utility from each of these two commodities as shown in the following table:

The table shows that a person can either spend all the five rupees on X or Y or divide these between the two. If he spends all the five rupees on X, the last rupee spent on X would give 10 units utility, but if that rupee is spent on Y (i.e., four rupees for X and one rupee for Y) he will get a greater amount of utility. So, he will substitute Y for X.

This process continues till the marginal utility of the last rupee spent on X and on Y will give him the same marginal utility, and he will attain this stage when he spends Rs. 3 on X and Rs. 2 on Y. At this stage, his total utility from his spending will become (25 + 20 + 16 = 61 units from X and 21 + 16 = 37 units from Y) 98 units and this will be the maximum amount of total utility that he can get from his spending. Thus, if a person equalises the marginal utility from each of his purchases, he gets the maximum amount of satisfaction. So, the doctrine of maximum satisfaction can be deduced from this law.

Consumer’s Equilibrium:

This law can also be explained in another way to show the optimum purchase of the consumer or the consumer’s equilib­rium. A consumer buys a commodity up to that amount at which its price is equal to its marginal utility. In the case of purchase of many commodities, maximum satisfaction requires the allocation of income in such a way that the marginal utilities of units of various goods bought are proportional to their prices.

In other words, if apples cost twice as much per kg. as potatoes, the consumer must adjust his purchases of these two goods until the marginal utility of a kg. of apple is twice as great as the marginal utility of a kg. of potatoes. So, in equilibrium, the marginal utilities of the different commodities purchased are proportional to their prices and these ratios of marginal utility to price must be equal to the common marginal utility of money.

If he distributes his expenditure rationally among commodities, X, Y, Z, etc., the following relationship will hold good in equilibrium:

MU of X/ Price of X = MU of Y/Price of Y = MU of Z/Price of Z = MU_M

where MU_M is the common marginal utility of money (i.e., marginal utility of a rupee).

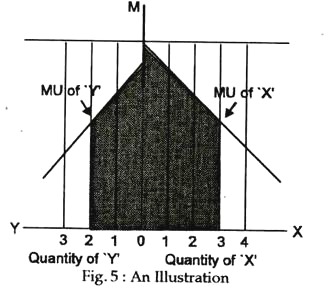
The equi-marginal principle can be illustrated in Fig. 5 to show the maximum satisfaction.

Fig.1 illustrates quantity consumed of two commodities, X shown on the right side and Y on the left side. The marginal utility curves for each use are also shown. The curve X is farther from the vertical axis (OM) than the Y curve to indi­cate the relatively stronger desire for X.

Let us suppose that a con­sumer has Rs. 5 to spend and P_X = P_Y = Re.1. Given the MU curves for X and Y the best allocation of his income is 3 units of X and 2 units of Y, because with these quantities the marginal utilities are equal. Any other allocations will lower the total satisfaction (the entire shaded area in the diagram).

Let us show it by devoting 4 units in X and 1 unit in Y. In such a case, the area between 3 and 4 under M U curve of X would be a gain, but there would be a loss of the area between 2 and 1 under the MU curve of Y. Clearly the loss is greater than the gain. Any other allocations excepting 3 units in X and 2 units in Y would give the consumer a lower total utility.

Application of the Principle:

The principle of substitution applies to production also. A producer varies the quantities of the different factors of production in such a way that he gets equal marginal returns from all the lines of expenditure. For this purpose, he will employ each factor up to that quantity at which the earning or price of each factor is equal to the value of marginal product of each factor. By doing so, he can produce at the lowest possible cost of per unit. As applied in production, this principle is known as the Law of Equi-marginal Returns.

Limitations:

The principle of substitution and the law of equi-marginal utility have the following limitations:

(i) Too much rationality:

The law of equi-marginal utility assumes too much rationality in the behaviour of a consumer. In real life, consumers do not always make their purchases considering minutely the relative marginal utilities of the different commodities; they make their purchases very often out of fancy or emotion or social needs without judging carefully their marginal utilities. In such cases the law does not hold.

(ii) Indivisible units:

The law does not operate in the cases of the goods which cannot be divided into small parts or are not available in small units (e.g., motor cars, refrigerators, TV sets, etc.). In such cases the perfect adjustment of marginal utilities is not possible and for this reason the law cannot be applied.

(iii) Mistake in calculation:

The law may fail to operate in the cases where consumers or producers commit mistakes in calculating marginal utility of the commodity or marginal product of the factor of production.

(iv) Difference between utility and satisfaction:

The law of equi-mar­ginal utility states that the equalisation of marginal utility in all the cases of purchases maximises total utility and thus total satisfaction of a consumer. But, it is pointed out that ‘utility’ and ‘satisfaction’ are not the same thing; so the maximisation of utility may not cause the maximisation of satisfac­tion. In answer to this criticism it is, however, pointed out that, although ‘utility’ and ‘satisfaction’ are not identical they are closely related; that an increase of utility would cause an increase in satisfaction cannot be denied.

(v) Difficulty in measuring utility:

The law assumes, as in the utility analysis of the neo-classical writers, that utility can be measured. But, it is pointed out that utility, being a subjective concept, cannot be measured.

(vi) Changing marginal utility of money:

Finally, the law assumes that the marginal utility of money remains constant at different levels of income. But as income increases marginal utility of money falls. So, the law cannot be applied in practice.