How to Reduce Risks in Business ?

We shall describe here three ways by which consumers and businesses may reduce risks. These are diversification, insurance and information.

Some of the important ways by which consumers and business may reduce risk are listed below:

Way # 1. Diversification:

Risk can be reduced by allocating one’s resources to a variety of risky situations. For example, a person may devote his available time to pursuing only one of many activities with uncertain returns, or he may allocate his time to a few such activities. It is often seen that his returns would be larger from the latter course than from the former.

Similarly, in the stock market, a person uses his resources to buy stocks with uncertain returns—prices of some stock may rise more than the others, and the prices of some stocks may even fall. Here, instead of buying only a few stocks, if he maintains a portfolio of a large number of stocks, he may prove to be a gainer.

Way # 2. Insurance:

Risk averse people are willing to pay to avoid risk. They may do this through buying insurance. In fact, if the cost of insurance is not more than the expected loss, risk averse people will buy enough insurance to recover fully from any financial loss they might suffer.

For example, a home-owner faces a 10 per cent probability that his house may get damaged by fire and in that case his financial loss will be Rs 50,000.

In this case, if the cost of fire insurance is not more than Rs 5,000, which is equal to the expected loss, then the person will go in for the insurance to avoid risk. For, in this example, by paying Rs 5,000 at most, he would be able to recover from a loss of Rs 50,000 if the fire actually occurs.

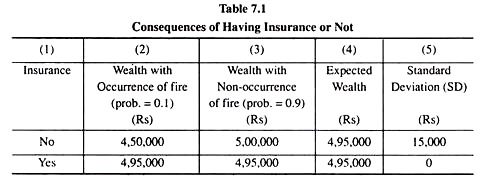
Let us explore this example further. Let us suppose that the house is worth Rs 5,00,000 and the cost of the said insurance is actually Rs 5,000. Here, if the person does not buy the insurance, his wealth would be reduced to Rs 4,50,000, if the fire actually occurs and it would be worth Rs 5,00,000 if there is no fire.

In this case, his expected wealth would be worth Rs (4,50,000 x 0.1 + 5,00,000 x 0.9) = Rs 4,95,000. Also here the SD of wealth would be

On the other hand, if the person buys insurance, then his wealth would be a certain Rs 4,95,000 irrespective of occurrence of fire (Rs 5,000 less owing to the insurance cost). In this case, the expected value of wealth would also be Rs 4,95,000, and the SD here would be zero.

We have arranged all these data in Table 7.1.

It is easily seen in the above table that the expected wealth is the same (Rs 4,95,000) in both the situations (of insurance coverage and non-coverage). The variability (given by the SD) of course, is quite different—with no insurance the SD of wealth is Rs 15,000 whereas, with insurance, it is zero. This gives us that the situation of no insurance involves more risk. In other words, insurance helps the person to reduce risk.

It is also obtained in our example that if there is no fire, the uninsured homeowner gains Rs 5,000 (which is the cost of insurance) relative to the insured owner of the house [column (3) of Table 7.1].

On the other hand, if there is a fire, the uninsured homeowner loses Rs 45,000 [Rs 50,000 (damage due to fire)-Rs 5,000 (cost of insurance)] relative to the insured homeowner. Let us remember that for a risk-averse person, losses count more (in terms of changes in utility) than gains. A risk-averse homeowner, therefore, will enjoy a higher utility by purchasing insurance.

Way # 3. The Law of Large Numbers:

In order to avoid risk, the risk-averse people will buy insurance. There are insurance companies that specialise in selling insurance. Now the question is, how does an insurance company bear the burden of risks of its customers, and yet make a profit. The answer lies in what is called the “law of large numbers”.

This law tells us that although the outcome of a single trial of a random experiment is unpredictable, the average outcome of a large number of trials of the experiment can be predicted. For example, the outcome of a single toss of an unbiased coin is equally likely to be a ‘head’ or a ‘tail’—we cannot predict it correctly.

But if we conduct a large number of such trials, we would be able to say that, on average, in half of the trials, ‘head’ would be obtained, and in the other half of the trials ‘tail’ would be obtained.

We may now apply these concepts to our example of fire insurance. In this example, the probability of occurrence of fire accidents is 0.1. The law of large numbers in this case would give us that for every 1,000 houses (equal in all respects), 100 houses, on average, would face fire accidents. But, in a particular sample of 1,000 houses, the number of houses experiencing fire may be as high as 120 (or more).

Therefore, if the owners of these 1,000 houses buy insurance, then the company would get Rs (5,000 x 1,000) = Rs 50,00,000 as premiums whereas it would have to pay Rs (50,000 x 120) = Rs 60,00,000 as compensation of damage due to fire. Therefore, in such a case, the insurance company would suffer a huge loss and it would go out of business.

On the other hand, if the company can sell insurance to a large number of homeowners (equal in all respects, for the sake of simplicity), if it sells to 20,000 buyers, then, due to the law of large numbers, there would be 2,000 cases of fire.

In this case, the company would receive as premium Rs (5,000 x 20,000) = Rs 100,000,000, whereas it would have to pay Rs (50,000 x 2,000) = Rs 100,000,000, i.e., here sufficient premiums can be generated from which losses can be paid. The insurance company can rely on the law of large numbers which ensures that the total payout will be not more than the total premium amount received.

Way # 4. Actuarial Fairness:

When the insurance premium is equal to the expected payout as in the above example, we say that insurance is actuarially fair. However, in order to cover administrative costs and make some profit, insurance companies have to fix up a premium rate which would generate an insurance fund that would be sufficiently larger than the expected losses.

This premium rate would be somewhat higher than what is actuarially fair. However, if there are a sufficiently large number of insurance companies so that the market is fairly competitive, the rate of premium will be close to the actuarially fair rate. In some countries, insurance premiums are regulated so that the buyers may be protected from paying excessive premiums.

Way # 5. The Value of Information:

People—the consumers and businesses both—often make decisions on the basis of limited information. If the information were more complete, then one could make better predictions and reduce risk. Since information is a valuable commodity, people would be willing to pay for it.

The value of complete information is the difference between the expected value of a choice when there is complete information and the expected value when information is incomplete.