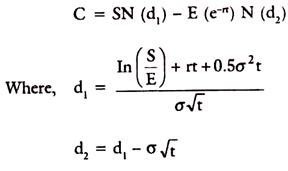Here is a term paper on ‘Option Trading’. Find paragraphs, long and short term papers on ‘Option Trading’ especially written for school and college students.
Term Paper on Options
Term Paper Contents:
- Term Paper on the Meaning of Options
- Term Paper on the Salient Features of Options
- Term Paper on the Types of Options
- Term Paper on the Options for Investors
- Term Paper on the Options for Speculation and Hedging
- Term Paper on Options Valuation
- Term Paper on the Settlement and Clearance of Options
- Term Paper on the Hedge Ratio (Black-Scholes Model) of Options
Term Paper # 1. Meaning of Options:
ADVERTISEMENTS:
It is a derivative security used for the purpose of risk management in the investment market, based on some security. Futures, forwards, swaps, options etc., are all examples of hedge instruments against risk. Investors are risk averse and want to reduce the risk. Individuals and corporations have a strong urge to reduce or manage risk and this is secured by trading in derivative markets.
The volatility in share prices required to be hedged. Thus, the larger the volatility the larger is the hedging demand. This is secured through the options and futures. Thus, the volume of future trading and volatility may be correlated but this does not mean that futures or options can cause higher or lower volatility in underlying shares/securities. These are all tools of risk management and no correlation is empirically found for options to increase or reduce volatility of share prices.
Term Paper # 2. Salient Features of Options:
The longest option period is 9 months but it can be for a shorter period of 30 days to 90 days. The expiration date is generally for March, June, September, and December, normally fixed for the second Friday of the month. The contract unit can be of 100 shares or stocks.
ADVERTISEMENTS:
The trading in these contracts can be fixed for a specific time period say 9 a.m. to 11.15 a.m. and 1.00 p.m. to 3.15 p.m. as in Tokyo or just for a couple of hours in a day. The last day of trading will be the business day prior to the second Friday in the expiration month.
The contract unit being 100 shares, the minimum trading unit can be fixed at 100 contracts. Instead of one exercise price, there can be many exercise prices at 50 point intervals of the index or of the underlying security price. The contract unit in Tokyo is 10,000 Yen multiplied by Topix.
There can be margin requirements for both customers and members. Customers may have to deposit transactions value of the option contract plus some percentage of the exercise price. Members have also to deposit some margins depending upon the option contracts sold.
If trading is done on margin account instead of cash account margins are imposed by the Regulators. There is unlimited risk on uncovered short options. These risks are generally covered by hedges and actual possession of securities. The amount of margin payable depends on premium market price and volatility of the scrip and a host of other factors.
ADVERTISEMENTS:
Characteristics of Options:
Derivatives have many distinctive characteristics:
1. Their origin is from some other security, commodity or a reference point, (such as indexes).
2. They are instruments of hedge against risk of undue volatility.
3. They are leveraged instruments for risk management based on original security or instrument.
Term Paper # 3. Types of Options:
Options are of two types, namely, call options and put options. Call option gives a right to buy without any obligation to buy put option gives a right to sell without any obligation to sell.
Options have varying characteristics depending on the underlying securities and indexes. The writer of an option is a stock broker member or a security dealer. The buyer of an option pays only a premium or a price depending on the risk of the underlying security and he is an investor or a dealer or trader.
The two major types of stock options are calls and puts. A call gives the investor the right to purchase 100 shares of a particular stock at a fixed price until a specific date. An investor who purchases a call option locks in a price on 100 shares of stock for a predetermined time. A put option gives an investor the right to sell 100 shares of a particular stock at a fixed price until a specific date.
ADVERTISEMENTS:
A put locks in a price at which to sell stock rather than a price at which to buy stock. Both puts and calls provide the investor with the right, but not the obligation, to use the option. Stock options are created, or “written”, by Member Brokers who wish to earn income from selling the options. The writers then become obligated to sell (if a call has been sold) or purchase (if a put has been sold) the stock if and when the owner of the option decides to exercise the put or call.
Puts and calls derive their values from the values of the stock that they are used to sell or purchase. Stock options pay no dividends or interest and expire without any value if not used by the expiration date. The value of a call option is directly related to the value of the underlying stock (i.e., the option value increases when the stock value increases) and the value of a put is inversely related to the value of the underlying stock (i.e., the option value increases when the stock value decreases). Option values are also affected by the time remaining until expiration, the price volatility of the underlying common stock and the market rate of the interest.
Term Paper # 4. Options for Investors:
To give an idea of how an investor benefits from the options, it is necessary to know the plus and minus features of these options. This can be demonstrated for two specific objectives of speculation and hedging, which are the common major use of options for investors.
ADVERTISEMENTS:
Options are a tool for the management of risk. A risk taker prefers the options to take advantage of speculation in the stock market. A risk averter also resorts to option as a hedge against risk. Options can also be used for inclusion in a portfolio for diversification of risk by the investor for a given level of return.
For simplicity, two examples can be given for its use for speculation and hedging.
Term Paper # 5. Options for Speculation and Hedging:
Let us’ say that Reliance is quoted at Rs. 230 at end of November 1999. A call option is written for Rs. 230 RIL February, 2000 at a premium of Rs. 30. The investor purchased the call option at Rs. 30 and paid Rs. 3,000, for 100 shares. If he would have purchased the actual shares, the cash amount paid would be Rs. 23,000.
ADVERTISEMENTS:
The interest on this amount for three months at a rate of 20% p.a. would work out to Rs. 1,150. The premium/price paid on option would work out to Rs. 3,000. The loss for this investment would be limited to Rs. 3,000 if the price has fallen below Rs. 300 per share.
In case the amount is borrowed, and invested in the cash market the loss would be Rs. 1,150, plus the actual price fall. Thus the loss is now limited and risk is known and calculated. But if the price goes beyond Rs. 230 let us say Rs. 260 before end of February, 2000 the option buyer has no profit or no loss. He paid for the option Rs. 30 and the exercise price of Rs. 230 plus premium paid Rs. 30 would just be covered by the actual price of Rs. 260.
But if the actual price of Reliance went upto Rs. 300 as compared to his price of Rs. 260 paid for the option, he will make a gain of Rs. 40 per share without taking delivery of share or and without shelling down Rs. 23,000 for the actual purchase of shares. This gain of Rs. 40 per share will give a gain of Rs. 4,000 per contract of 100 shares and on an investment of Rs. 3,000. This is clear speculative gain of 133% on a calculated risk.
The investor can look into the market behaviour of the share and of the high/lows of the past month and year. Thus, over year Reliance recorded a price range of Rs. 161 (low) to Rs. 303 (high). In this background if the investor is bullish, he will even buy the call option of RIL Rs. 300 at a price of Rs. 50.
Suppose the investor is bearish and wants a hedge against future fall in price, as he holds Reliance in his portfolio, then he buys a put option. Let us say RIL February, 2000 is quoted say Rs. 300 at a premium of Rs. 20. If the contracted shares of 100 are sold in cash market he gets Rs. 30,000 but if he buys a put option he pays only Rs. 2,000.
If the actual market price is, let us say Rs. 260 the investor can exercise his option to sell and get Rs. 300 per share and after deducting the premium paid Rs. 20 per share, he still gains Rs. 20 per share in this deal. Here the investor has protected his portfolio from a further loss if Reliance share prices fall more, before end of February, 2000.
ADVERTISEMENTS:
An investor can buy both a call option and put option for limiting his risk and trade in options market. Thus, RIL call Rs. 300 February 2000 @ Rs. 30 (premium). Bought 100 calls and R.I.L. put Rs. 300 February 2000 at Rs. 20 (premium) bought 100 puts.
The range of price in which he is protected from risk is Rs. 330 at high and Rs. 280 at low. He paid Rs. 50 per share for this option position. Alternatively an investor may buy in the cash market at Rs. 300 per share and cover his risks by buying a put option R.I.L. 320 February 2000 at a price of Rs. 20.
Various combinations of puts and calls along with or without deals in the cash market can provide the necessary hedge to the investor. Hedging in the options market can be by taking the opposite position in the cash market. Hedging in the options market itself is called spreading (Bull spread or Bear spread).
Thus, an investor can plan for speculation pure and simple or for calculated hedge of risk or for portfolio management, if he is operating in the options market.
Term Paper # 6. Valuation of Options:
ADVERTISEMENTS:
Basically, the value of option is related to the value of the underlying security. The value differs with time before the expiration and at expiration.
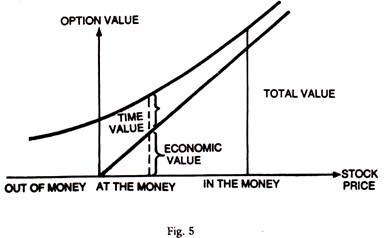
The value of the stock option has three different zones, as shown below:
(i) Out of the Money:
Where the stock price is below the exercise price.
ADVERTISEMENTS:
(ii) At the Money:
Where it is close to or at the exercise price.
(iii) In the Money:
ADVERTISEMENTS:
Where the stock price is above the exercise price.
These zones are depicted in the chart below:
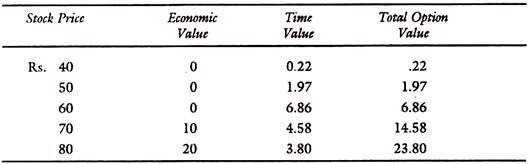
Say the exercise price is Rs. 60. If the stock price is below 60, there is no economic value. There is only time value; if stock price soars above Rs. 60 it will have both economic value and time value. As seen from the chart time Value is maximum, when the exercise price and stock price are the same but is lower below the exercise price or above it.
If the actual price is lower than the exercise price there is less chance of profit on the call. If the actual price is above the exercise price, then there is a chance of profit, and there is less reason to pay a premium over the economic value (intrinsic value).
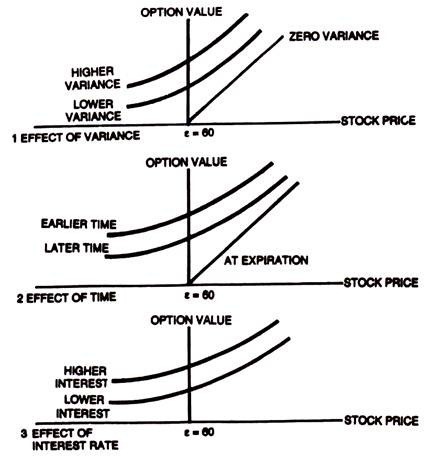
Factors Affecting the Option Value:
There are normally several factors which influence the option value.
The more important of them are:
(1) Expected variance in price or return of the underlying stock,
(2) The time to expiration,
(3) The level of interest rates, and
(4) The dividends and fundamentals of the stock.
Leaving aside the fundamentals of the stock and dividends paid, which will generally be reflected in the actual stock price, the influence of other factors are explained in the diagrams below:
Term Paper # 7. Settlement and Clearance of Options:
An agency like Options Clearing Corporation (OCC) has to be set up and the members of which can write options and trade in them. Members are normally registered stock brokers or security firms. The OCC will lay down the rules and regulate the trading in options through imposition of margins, deposit of underlying securities and settle disputes. The OCC will also provide the facilities for settlement and clearance in the contracts in options, as in the case of the stock exchange for contracts for hand delivery and those for clearing as at present regulated.
The OCC will govern the terms for writing the contracts, trading hours, expiration dates, exercise dates and related matters for the options. Finally, at the end of trading on last day, the settlement and clearance facilities are also extended by this corporation through computerised EDP and netting procedures.
The rules governing the writing of the options trading in such contracts, exercise dates, expiration dates etc., are all governed by such controlling body.
As in the case of the regular stock exchange activity involving the regulation of trading and of the members’ activities in securities trading, the control of options trading is to be entrusted to a separate body regionally or on an all India basis. The final control of all the self-regulatory bodies such as options control corporations rests with the Securities and Exchange Board. The regular stock exchanges, the NSE and the OTC exchange are formulating the rules for implementing them in India.
Term Paper # 8. Hedge Ratio (Black-Scholes Model) of Options:
Take numerical example to explain the hedge ratio.
The option values for each stock price are given in the table below:
Option Value — Exercise Price Rs. 60
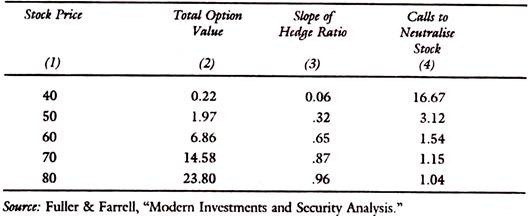
Hedge Ratio Data:
The slope of the Hedge ratio will depend upon the price level. As the price of the stock rises above the exercise price, the slope will approach 1, but if price falls below the exercise price, it will approach zero. The column 4 is the reciprocal of the slope in column 3.
It will tell the number of short call options that will neutralize the long position in the stock.
Black-Scholes Formula:
The operations involving the hedge is the vital part of the Black Scholes Option Valuation Model. The long position in the option can be hedged by a short position in the stock and vice versa. By hedging perfectly, any profit resulting from an instantaneous increase in the price of the stock would be exactly offset by an instantaneous loss on the option position and vice versa.
Black Scholes formula can be used to hedge the market risk of stock portfolio by proper option strategy. Because we can reach a theoretically riskless position, one can earn a risk free return, by such hedging — that is, the short-term interest rate is the fair value of the option. The option price would adjust to the fair value under equilibrium conditions.
If C is the equilibrium value of option, the formula given by Black-Scholes is as follows:
Where,
S= Current market price of underlying stock
E = Exercise price of the option
r = Risk free rate of return (Continuously compounded)
N (d) = The value of the cumulative normal distribution evaluated at ‘d’.
t= Time remaining before expiration
σ = Risk of the underlying common stock measured by standard deviation. N (d1) cumulative density function of d1 and similar is N (d2). N (d1) and N (d2) denote the probabilities that deviations of less than d1 and d2 respectively will occur in a normal distribution that has a mean of ‘o’ and a standard deviation of 1.
Mathematically ‘e’ is the base of natural logarithms and is approximately equal to 2.71828. This means that E/eRT is the present value of the exercise price, when a continuous discount rate is used (it is analogous to E/(l +R)T or E (e-rt) used in the formula. The present value of the exercise price, using a discrete discount rate.
The quantity In (S/E) is the natural Logarithm of S/E.
Note:
Values of N (d) for various levels of and a pocket calculator for estimating the fair value of option are necessary to use Black-Scholes Formula.
Impact of Dividends:
Dividend affects the value of the call and the timing for exercise of the option. Take the European Types of option, which is not dividend protected. If the dividend is paid on the underlying stock during the contract period, then the value of the call stands reduced to that extent. One approach to this problem is to treat all the expected future dividends upto the expiration date as paid. The present value of these dividends is subtracted from the current market price of the stock and the adjusted price is incorporated in the Black-Scholes Model. This ensures that the fair value of the call reflects the presence of dividend on the underlying stock.
In the American type of options, there is an obvious advantage in exercising the option before the ex-dividend date and buying the stock in time to receive the dividend. In this case also, B.S. Model can be used provided the Current Market Price is netted for the present value of the expected future dividends upto the date of expectation.
Implications:
Black-Scholes formula is a static analysis. The formula shows that the fair value has the following major inputs:
Common stock price, exercise price, time to maturity, market interest rate and standard deviation of annual price changes.
The implications of the formula are:
(1) The higher the price of the underlying stock, the higher is the value of call option.
(2) The longer the time to expiration date (t) the higher is the value of the call option.
(3) The higher the exercise price, the lower the value of call option.
(4) The higher the risk free rate, the higher is the value of call option.
(5) The greater the risk (σ) of the common stock, the higher is the value of the call option.