W.J. Baumol examines what happens if the firm adopts an alternative objective—the maximisation of the value of its sales (total revenue) under the requirement that the firm’s profits should not fall below a minimum acceptable level.
Sales maximisation implies maximisation of total revenue not obtaining the largest possible physical volume, because at a zero price physical value may be infinite but rupee sales volume zero. In fact, there is a well-deter- mined output level which maximises rupee sales.
In short, total revenue is maximum where marginal revenue = 0, i.e., elasticity of demand = 1.
We know that if Ep > 1 TR increases, if price falls and MR is positive. If Ep = 1 TR is constant whether price rises or falls and MR=0. Finally, if Ep < 1 TR falls when price falls and MR is negative.
ADVERTISEMENTS:
The above condition now replaces the familiar MC = MR profit- maximising rule.
Sales Maximisation subject to the Profit Constraint:
As Baumol says, “If at the revenue-maximising output the firm does, in fact, earn enough or more than enough profits to keep its stockholders satisfied then it will want to produce the sales-maximising quantity. But, if at this output profits are too low, the firm’s output must be changed to a level which, though it fails to maximise sales, does meet the profit requirement.”
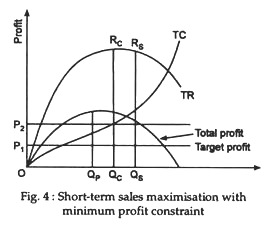
So, two possible equilibria may emerge: one in which the profit constraint does not provide an effective barrier to sales maximisation, and one in which it does. This is shown in Fig. 4.
The profit and sales-maximising outputs are, respectively, OQp and OQs. Now if, for example, the minimum required profit level is OP1, then the sales-maximising output OQs will provide plenty of profit and that is the amount it will pay the sales maximiser to produce.
His selling price will then be set at QsRs∆OQs. But, if the producer’s required profit level is OP2, output OQs, which yields insufficient profit, clearly will not do. Instead, his output will be reduced to the OQc, level which is just compatible with the above profit constraint.
The profit-maximising output, OQp, will usually be smaller than the one which yields either type of sales maximum, OQs, or OQc. And at the points of maximum profit marginal cost must equal marginal revenue. For marginal cost is normally a positive number. Hence marginal revenue will also be positive when profits are at a maximum, i.e., a further increase in output will increase total sales (revenue). Therefore, if at the point of maximum profit the firm earns more profit than the required minimum, it will pay the sales-maximiser to lower his price and increase his physical output.
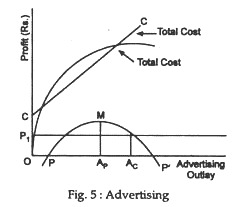
The decision as to how far to carry advertising expenditure, if not entirely, is largely influenced by the firm’s choice of objectives— whether it chooses to maximise sales or profits. This point has been illustrated by Baumol with the aid of Fig. 5. Here, the horizontal axis represents advertising expenditure and the vertical axis total sales (revenue) and total profit.
The total revenue curve is drawn on the basis of the practical assumption that increased advertising expenditure can always increase physical volume, though after a point sharply diminishing returns may set in. The implication is that total revenue must vary with advertising expenditure in precisely the same manner for unlike a price reduction, a rise in advertising expenditure, all other things remaining constant, involves no change in the market value of the items sold.
Hence, whereas an increase in physical volume produced by a price reduction may or may not increase rupee sales, depending on whether demand is elastic or inelastic, an increase in volume brought about by additional advertising expenditure must always be accompanied by a proportionate increase in total sales revenue or turnover.
If we add all other costs to advertising cost, we get the line which depicts the firm’s total (production, distribution, and selling) costs as a function of advertising expenditure. Subtracting these total costs from the level of rupee sales at each level of advertising outlay, we obtain a total profits curve PP’.
It is observed that the profit-maximising expenditure is one at which PP’ attains its maximum, M. If, on the contrary, the sales maxi-miser’s minimum acceptable profit level in OP1, the constrained sales-maximising advertising budget level is OAc. The important point to note here is that there is no possibility of an unconstrained sales maximisation. For, by assumption, unlike a price reduction, increased advertising always increase total revenue.
Consequently it will always pay the sales maximiser to increase his advertising expenditure until he is stopped by the profit constraint—until profits have been reduced to the minimum acceptable level. The implication is that sales-maximisers will normally advertise no less than, and usually more than, do profit-maximisers.
For unless the maximum profit level ApM is no greater than the required minimum OP1, it will be possible to increase advertising somewhat beyond the profit-maximising level OAp without violating the profit constraint. Furthermore, this increase will be desired since, by assumption, it will increase physical sales and with them, rupee sales will rise proportionately.
The interrelationship between output and advertising decisions now enables us to see why an unconstrained sales-maximising output OQp (Fig. 5) will ordinarily not occur.
To quote Baumol, “For if price is set at a level which yields such an output, profits will be above their minimum level and it will pay to increase sales by raising expenditure on advertising, service, or product specifications. This is an immediate implication of the theorem that there will ordinatily be no unconstrained sales- maximising advertising level. Since its marginal revenue is always be used to increase sales up to a point where profits are driven to their minimum level.”