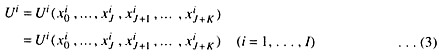The first clear formulation of a theory of public expenditure which can give a positive interpretation was presented by poter krut Wicksell and Esik Lindahl. In this formulation, individuals bargain over the level of public goods supply, simultaneously with the distribution of the cost between them. The bargaining equilibrium is Pareto optimal. In addition, each individual pays a price in terms of private goods—which is equal to his marginal willingness to pay.
Voluntary Exchange Model:
It is an approach to the analysis of the provision of public goods which seeks to establish conditions under which these goods can be provided on the basis of unanimous agreement— i.e. without coercion. This may be contrasted with the generally observed arrangement that the provision of public goods is financed by compulsory taxation and not by voluntary agreement.
The voluntary approach was first advanced by Knut Wicksell who argued that:
(i) Each public good should be financed by a separate, identifiable tax.
ADVERTISEMENTS:
(ii) The unanimous agreement of all members of the society would be required to decide on the amount of the good to be supplied.
At the outset individuals would be aware of their allotted share of any tax to be levied. The problem would then be to decide the level of provision. The analysis was extended by Lindahl, who presented a model in which both the share of taxes and the amount of good were open to debate.
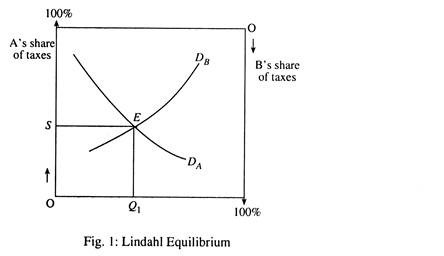
In Lindahl’s model, equilibrium requires each individual to pay a tax rate just equal to the individual’s marginal utility from the good. This can be shown for a two-person community (consisting of A and B) in Fig. 1 which has quantity of public good along horizontal axis and the share of tax paid by A and B along vertical axis.
A’s share of taxes increases from the bottom to up and S’s share of taxes increases from top to down. The schedule DA indicates the amount of the good A will wish to demand at different levels of his tax share. As his share of the cost goes down, his desired level of provision increases. DB indicates B’s preferences—again, as his share of the cost falls, his preferred quantity of the good increases. The Lindahl equilibrium involves producing Q1 of the good with tax shares as indicated at point S.
ADVERTISEMENTS:
In the Lindahl model, public goods are provided in a manner which ensures everyone gains from their provision i.e. The provision of goods is always a Pareto improvement. Lindahl’s analysis adds the condition that each individual consumes his most-preferred or ‘optimal’ amount of the public good given his tax share.
Despite the appeal of the model, difficulties arise in its application. In particular, the problems of reaching unanimous agreement and the possibility that individuals will not indicate true preferences (i.e. they may seek to be free riders) undermine the usefulness of the model.
Let π ij+k be the price which individual i pays for public good K and let Pj + k be the producer price or marginal cost. Then the Lindahl equilibrium would be characterised by the condition:
Thus, at first glance, the concept of a Lindahl equilibrium seems to establish an analogue to the competitive markets for private goods with the interesting difference. That the prices should differ from one individual to the other, depending on his marginal willingness to pay.
This also ties in with older notions of the benefit theory of taxation, according to which taxes were seen as payments for public goods to be levied in accordance with the benefits which each individual derived from them.
There is an interesting duality between the definitions of private and public goods on one hand and properties of equilibrium prices on the other. In terms of quantities, for private goods the sum of individual quantities consumed add up to the quantity produced, while, for public goods, individual consumption equals aggregate production. In terms of prices, on the other hand, for private goods each consumer price equals producer price, while for public goods individual consumer prices add up to producer price.
There is, however, one crucial difference between a Lindahl equilibrium and a competitive equilibrium for private goods. With private goods, individuals facing given prices have clear incentives to reveal their true preferences by equating their marginal rates of substitution to relative prices, at least if the economy is sufficiently large relative to the individual. Without paying, the individual is excluded from enjoying the benefits of consumption.
With public goods this no longer holds. Because an individual has the same quantity of public goods available to him whether he pays or not, he has an incentive to misrepresent his preferences and to be a free rider on the supply paid for by others. Moreover, this problem is likely to be particularly severe when the number of individuals is large, since his own contribution will then make little difference to the total supply.
The equilibrium of Lindahl model is not compatible with individual incentives to reveal preferences truthfully; for this reason Samuelson (1969) has referred to the individual Lindahl prices as pseudo-prices and to the equilibrium as pseudo-equilibrium.
In this case, one would conjecture that because all individuals have the same incentives to understate their true marginal willingness to pay, the Lindahl mechanism would result in equilibrium levels of public goods supply which would be too low relative to the optimum.
But there is really no need to associate the problem of preference revelation with this procedure alone; as another extreme, one might think of the case where individuals are asked to state their preferences on the assumption that the cost to them is completely independent of their stated willingness to play, but there is a positive association between this and the quantity supplied.
Then there will be incentives to exaggerate the willingness to pay and a consequent tendency towards over-supply. Thus, the general problem which arises is how to design a mechanism that will allow the decision-maker to implement the efficiency condition. The development (1954-55) by Paul Samuelson of the modern theory of public goods must be counted as one of the major breakthroughs in the theory of public finance.
ADVERTISEMENTS:
In these two very short papers Samuelson posed and partly solved the central problems in the normative theory of public expenditure:
(i) How one can define goods analytically that are consumed collectively, that is for which there is no meaningful distinction between individual and total consumption?
(ii) How one can characterize an optimal allocation of resources to the production of such goods?
(iii) What can be said about the design of an efficient and just tax system which will finance the expenditures of the public sector?
ADVERTISEMENTS:
What is required is a satisfactory theory of market failure. Criteria for just taxation had developed independently of any analysis of the expenditure side of the public budget. Still, Samuelson’s formulation was a great leap forward, presenting an integrated solution to all three problems.
The Samuelson Model:
The aim of the model is to derive conditions for optimal resource allocation in an economy in which there are two types of goods—private and public. It is worth emphasizing that these terms do not prejudge the respective tasks of the private and public sectors; the analysis at this stage is institution-free and can best be considered as representing the problems of a planner who knows the production possibilities of the economy, the preferences of the consumers and his own ethical values.
The nature of the two types of goods are defined by the equations which give the relationship between individual and aggregate consumption. For private goods, the total quantity consumed is equal to the sum of the quantities consumed by the individuals, so that
ADVERTISEMENTS:
where the superscript refers to individuals and subscript to commodities.
For public goods the corresponding relationship is one of equality between individual and total consumption:
Individual preferences, represented by utility functions, are then defined over the quantities consumed of private and public goods, so that we can write the utility of individual i as
The definition (2) has given rise to some confusion and controversy. Are there actually any goods which can be described by this definition? The usual answer is that there are some cases pure Public good ,national defence, which can indeed be so described in such cases consumer benefits are directly related to the total availability of the good in question and the consumption benefits of any one individual do not depend on the benefits enjoyed by’ the others.
ADVERTISEMENTS:
This property of public goods is usually referred to as non-rivalry in consumption given the supply of the good in question, the consumption possibilities of one individual do not depend on the quantities consumed by others as they do in case of private goods However many goods which it is natural to think of as public, turn out on closer inspection to have elements of rivalry.
A road may satisfy the definition of a public good as long as the traffic is low, but with higher density and consequent congestion this will no longer be the case. Accordingly, several studies have been devoted to the analysis of ‘impure’ public goods, combining in same way the properties of private and public goods in the original Samuelson definition
The Samuelson formulation does not assume that the benefits derived from the supply of the public goods are the same for all, even though availabilities are the same. Neither does it assume that the benefits from public goods are independent of the quantities consumed of private goods.
And the elements of rivalry in the road congestion example may be captured by introducing externalities in the consumption of a private good-car use-whose benefits depend on the supply of a public good-the road. Thus, the original Samuelson formulation offers great flexibility of interpretation, and we have been provided with an answer to the first or the main problems.
We now turn to the problem of optimality of resource allocation and begin by characterizing a Pareto optimum for this kind of economy. Since the interesting special features of the model are on the consumption side only, we assume that the conditions for efficient production are satisfied, so that the production possibilities for the economy can be summarised in transformation or production possibility equation
F(x0, …xJ ,xJ+i ,…xJ+K) = 0 … (4)
ADVERTISEMENTS:
The problems of Pareto optimality may now be formulated as follows: of all allocations satisfying equation (4), find the allocation which maximises utility for consumer 1, given arbitrary but feasible utility levels for all other consumers.
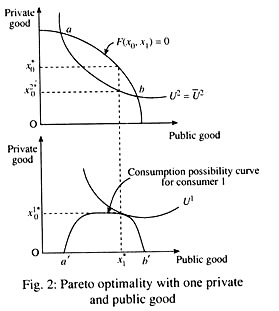
As shown (1955) by Samuelson, the solution can be given an instructive graphical solution in two-dimensional case. We, therefore, begin with the case where there are two consumers and one private and one public good.
In good the upper panel of the figure we have drawn the production possibility curve as well as an indifference curve corresponding to the fixed level of utility for consumer 2; since the two curves intersect, there are obviously a number of allocations which satisfy these two constraints. In the lower panel, the curve ab shows the consumption possibilities for consumer 1, the points a and b corresponding to the points of intersection in the upper panel.
For any point on U2 between a and b, it must be the case that two individuals consume the same amount of public good, while consumer 1 ‘s private good consumption is equal to the vertical difference between the production possibility curve and consumer 2’s indifference curve.
The best allocation from 1’s point of view is then given by the tangency between his highest attainable indifference curve and consumption possibility curve in the lower panel. This determines the optimum supply of the public good (a,*) and consumer l’s consumption of the private good (x10*) as well as consumption of consumer 2 (X2/0*).
The slope of consumption possibility curve must, of course, be equal to the difference of the slopes of the two curves from which it is derived. The tangency point can, therefore, be characterised in terms of marginal rates of substitution and transformation as
In words, the sum of the marginal rates of substitution should be equal to the marginal rate of transformation between the public and private good. Or, since the private good may be taken as a numeraire commodity, the sum of the marginal willingness to pay for the public good should be equal to the marginal cost of production.
The intuition should be clear: an extra unit of supply benefits both consumers simultaneously; to find the total marginal benefit we have to take the sum of the marginal benefits accruing to all consumers. Problem (ii) has been solved.
The Samuelson theory of public goods has been of decisive influence for the theory of public expenditure. One of the results of this is that the normative theory of public goods has become much more satisfactory from a theoretical point of view than the positive theory. This state of affairs may, in-fact, be unavoidable.
The normative theory has little need to model institutional details and can thus be given a more unified appearance. A positive theory, on the other hand, must model institutions, and there is no single institution corresponding to the competitive market in the private goods case which can serve as a unifying benchmark.
Moreover, development of the positive theory of public goods must necessarily be closely tied to the progress of the positive theory of public sector behaviour in general; it will be interesting to see whether this theory can be developed to provide models both realistic and reasonably simple.