Index Number of Prices: Meaning, Uses and Limitations

Let us study about the Index Number of Prices. After reading this article you will learn about: 1. Meaning of Index Number of Prices 2. Method of Constructing an Index Number of Prices 3. Uses 4. Limitations.

Meaning of Index Number of Prices:

An index is a number which shows how average of commodity prices (wholesale or retail prices), wages, etc., change over time. Index numbers are expressed in absolute form. An index number of prices is an index of the prices of goods and services bought by the household.

An economy produces a large number of different products. The price change of each commodity is expressed typically in percentage terms and then the average of the price changes of these commodities is calculated. This will enable us to compare the price movements over different time periods.

Time series data are expressed in terms of index numbers. If we want to get the index number of prices of2009 relative to that of 2005, we calculate the ratios of 2009 prices to 2005 prices for each product that the economy produces, then average of all those ratios is obtained.

A simple example will help our understanding. Suppose, we live in a primitive two-good economy—bread and cloth. Now, we want to know whether price movements have taken place in this economy between 2005 and 2009. If the price of bread (P_b) doubles between 2005 and 2009 while price of cloth (P_c) remains unchanged, then the average of the two price ratios would be

P_b in 2009/P_b in 2005 = 2, and P_c in 2009/P_c in 2005 = 1

The average of these two ratios is:

(2 + 1)/2 = 1.5

This means that the general price level has gone up by 50 p.c. between 2005 and 2009. This is how the index number of price is calculated.

Method of Constructing an Index Number of Prices:

To measure the extent of changes in the value of money we construct index number of prices. An economy does not produce two goods— rather, it produces a variety of products. Suppose that we wish to know how much price level changes between 2007 and 2009 for all the goods produced.

The steps for preparing an index number of prices are:

(a) Choice of Base Year:

A base year is to be selected. Base period or base year is also called ‘reference date’. Since we want to know the changes in the value of money from 2007 to 2009, base period is the 2007.

Two desirable criteria for the selection of reference date or base year are:

(i) The period should show economic stability—a period which is rather vaguely called ‘normal period’, and

(ii) It is not too distant from the given period or current period (here 2009).

(b) Selection of Commodities:

The second step is the selection of a ‘basket of goods’ that a typical family consumes out of its income and spending habits. Suppose, we are interested in measuring the changes in the living standards of industrial workers.

Thus, one should select only those commodities which are generally consumed by the working classes. Since it is impossible to include all the commodities, we only select representa­tive commodities. Further, the number of commodities to be chosen should neither be too small nor too large.

(c) Collection of Data:

Thirdly, data collection is another important step. Price quotations for the selected commodities must be accurate and comparable. Further, selected prices (both wholesale and retail) should be representative of a large volume of transactions.

For the construction of wholesale price index numbers for general purpose, the wholesale price quotations for an adequate number of commodities should be obtained. For the purpose of construction of consumer price index numbers for a special purpose, the retail prices of commodities are required to be collected, although information about retail prices is difficult to obtain.

(d) Selection of the Average:

Base period index is set at 100. In other words, the average of the numbers for the base year should always be 100. The current year will then show deviation from the base year. If the deviation is 100 plus, then we say that the price level has risen; and if the deviation is minus 100 then it suggests that price level has gone down.

Since we know that for some commodities price relatives will be 100 plus and for others price relatives will be 100 minus, it is necessary to compute the average of all price relatives. There are various statistical measures of computing averages. These are arithmetic mean, geometric mean, harmonic mean, etc. The most widely used average is arithmetic mean.

(e) Assigning Proper Weights:

A vital step in calculating any index is to allocate each item a weight to signify its importance.

Un-weighted average has limitations. Not all commodities consumed are of same impor­tance to all people. People may attach more importance to necessities than luxuries. Thus, to measure the relative importance of different commodities, different weights are to be assigned to different commodities so as to obtain greater accuracy in the result.

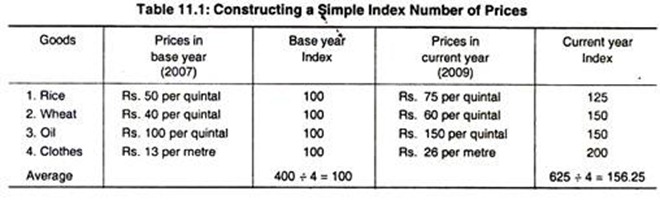
The method of calculation is illustrated in Table 11.1. We use imaginary figures and include only four commodities for the sake of simplicity.

One may conclude that prices in 2009 are 56.25 p.c. higher than 2007. If we want to calculate prices in subsequent years, we would express it as percentages of those in 2007 (the base year) and average it in a similar manner.

Weighted Index Number of Prices:

The simple average price ratios described above is misleading since same weight has been assigned to every commodity. This means that all commodities are of equal importance. A 10 p.c. change in the price of wheat has the same impact on the index as a 10 p.c. change in the price of clothes.

But we know that the changes in the prices of wheat and clothes by a certain percentage will not affect all consumers in the same way. Thus, weights are to be assigned to different products according to their importance to an average consumer. Index number of prices with weights attached to different products is called weighted index number of prices.

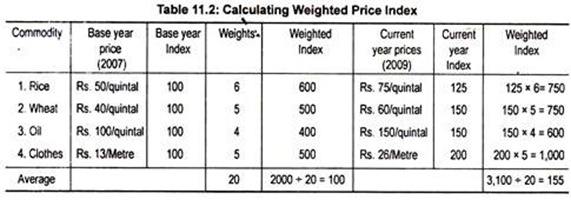
We allocate weights for different commodities. Then price indices for each good and for each year are multiplied by the appropriate or assigned weights and then average is obtained by dividing the total of these weighted indices by the total of the weights.

Table 11.2 illustrates weighted index number of prices.

The average price increase, after attaching weights to different commodities, is now 55 p.c., rather than 56.25 p.c. in the earlier example.

Uses of Index Number of Prices:

Index numbers may be constructed for indicating the average changes generally with regard to a wide range of business or economic activities or may be constructed to indicate changes as to one or a few aspects of business or economic activities. A general index number of price covering all goods and services no doubt will serve a useful purpose in analysing economic and business activities.

The importance or the uses of index numbers of prices are listed:

(a) Measures Changes in Price Level and Standard of Living:

Index number of prices is a method through which we can measure changes in the price level over time. This means that whether a country faces inflation or deflation can be known from the index number of prices. Thus, it helps to determine the changes in the economic conditions of people.

Inflation reduces standard of living while deflation increases living standards. However, this statement is too simplistic and ignores many aspects. Anyway, as the price index changes, per capita income changes. A change in per capita income causes a change in the standard of living.

(b) Regulation of Wage Rate:

Salaries and wages and dearness allowances are revised by the government when price level changes. Higher wages and dearness allowances are often given by the appropriate authorities when index numbers of prices rise so as to protect the real income of the workers.

In other words, a fall in real income consequent upon a rise in price level measured by the index numbers of prices is compensated in the form of higher wages and dearness allowances. Cost of living index can be made a basis for the regulation of wage rates and other allowances.

(c) Determination of Government Poli­cies:

Index numbers of prices serve as guide to government policies. The price stability objective of the government policy is based on index numbers. It formulates policies to control inflation and deflation. Index numbers also enable governments to explain their population policies, agricultural and industrial policies, taxation policy, etc.

In addition, index numbers serve as a guide to the central bank (i.e., monetary authority) to take appropriate action against price changes.

(d) Guide for Businessmen:

Index numbers also serve as a guide to business­men. Rising prices as indicated by index numbers may create an atmosphere of optimism. Now these people will be interested in investing more to have larger profit. Opposite reaction follows when prices fall.

(e) International Comparisons:

An index number facilitates international compari­sons of economic variables. For instance, we want to make comparisons in living standards between different nations. We then construct real per capita of incomes of different nations on the basis of index numbers of prices. Thus, index numbers measure the levels of development of different countries.

Limitations of Index Number of Prices:

The construction of index numbers creates some theoretical and practical problems. Since these problems cannot be accurately solved, the method of index numbers of prices loses its utility.

These problems are:

(a) Choice of a Base Year:

The first major problem is concerned with the choice of a base year. Two criteria for the selection of’ base year are that it must show economic stability and it must not be too distant from the given year. The base period must not coincide with abnormally high or low prices. But it is very difficult to get a ‘normal year’ free from any economic disturbances.

Further, if the base year is too distant from the current year, it is possible that the pattern of consumption may change considerably. New types of commodities may be introduced and consumers may change over to these types of commodities which are not comparable with the similar types used in the base period.

(b) Problem of Averaging of Prices:

An index number is a summary measure. Thus, its usefulness decreases as it tries to describe a complex situation which is too wide in scope.

The arithmetic mean or any other form of averages becomes less and less represen­tative. Such averaging is beset within certain technical difficulties. Some people reco­mmend arithmetic mean while others recommend geometric mean. Proper method of averaging is, thus, not obtainable.

(c) Difficulty of Obtaining Correct Data:

Data or statistics collected are often unreliable and less accurate. As a result, estimates based on such data are bound to be unreliable.

(d) Difficulty in the Selection of Prices:

There are two prices—wholesale and retail. Should we select retail prices or wholesale prices? General Price index is based on the wholesale prices which are easy to collect. But as far as consumers are concerned, retail prices are more relevant.

While constructing index numbers of prices, retail prices should be taken into account. But it is difficult to collect reliable and accurate statistics relating to retail prices. Retail prices vary from market to market. Retail price index is, thus, difficult to construct.

(e) Difficulty in the Selection of Commo­dities and Choice of Weights:

The basket of goods and weights given to them are merely arbitrary. Basket of goods that are chosen is based on current spending habits and incomes of consumers. Different classes of people buy different kinds of goods. Therefore, it is difficult to choose all kinds of commodities.

However, to tackle this problem, we ought to construct a separate index number for the different groups of people. Even then, problem exists since most commodities are subject to frequent changes in quality. Where a price change suggests an improvement in quality of the product one may face trouble in assessing the real nature of the price change.

Further, the compiler of the index number makes any arbitrary decision with regard to weighting. Now for two persons or households the assigned weight will be exactly the same. The chosen basket of goods is only applicable in the base year. But as incomes or tastes and fashions change, demand for goods changes. And weights assigned to these goods are likely to be arbitrary.

Despite its limitations, an index number is the most useful means of measurement of changes in the value of money—at least in the short run. It is merely an approximate indication of changes in the cost of living.

Even if a highly sophisticated statistical technique is employed to measure the changes in the value of money it will not be perfectly exact and accurate. Some sort of arbitrariness and inaccuracy will creep in. That is why it provides approximate indications.