How Price of a Good is Determined in the Market?

This article will guide you about how price of a good is determined in the market.

In a perfectly competitive market, the number of buyers and sellers is large. The buyers and sellers are in competition to buy and sell a homogeneous product. The number of buyers and sellers in such a market is so large that each of them buys or sells a negligible fraction of the total quantity bought and sold in the market. As a consequence, none of them has any indi­vidual influence on the process of price determination.

In a perfectly competitive market, equi­librium price of the product is determined through a process of interaction between the aggre­gate or market demand and the aggregate or market supply. Equilibrium price is such a price at which the market demand becomes equal to market supply.

If, at any particular price, demand and supply are equal, the buyers and sellers both remain satisfied, for, at the said price, the sellers supply what the buyers demand, and the buyers demand what the sellers supply.

There­fore, the buyers and sellers accept this price, and they buy and sell accordingly. None of them is dissatisfied, and so, none of them would want a change in the price. That is why this price is called the equilibrium price.

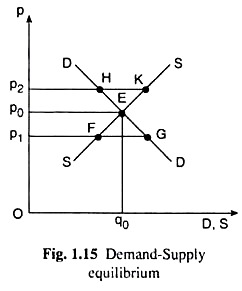
The process of price determination is explained as a matter of interaction between de­mand and supply with the help of Fig. 1.15. The DD curve in this figure is the aggregate or market demand curve for the product. This curve tells us what is the aggregate demand of the buyers at any particular price, and, as such, this curve is the horizontal summation of the indi­vidual demand curves of all the buyer.

For example, from the DD curve of Fig. 1.15, at the price p = p₂ the market demand for the good is p₁G. Again, at p = p₂, the market demand amounts to p₂H. Owing to the law of demand, the individual demand curves are downward sloping towards right.

That is why the market demand curve as a horizon­tal summation of the individual demand curves would also be downward sloping towards right (or negatively sloped).

On the other hand, the SS curve in Fig. 1.15 is the aggregate or market supply curve for the good. From this curve the market supply of the good at any particular price, and so, this curve is the horizontal summation of the individual supply curves of the sellers. For example, from the supply curve SS, at p = p₁, the market supply of the good is p₁F or, at p = p₂, the market supply is p₂K.

Since the supply curves of individual sellers are sloping upward towards right owing to the law of supply the aggregate supply curve as the horizontal summation of the individual supply curves would also be sloping upward towards right or positively sloped like the SS curve in Fig. 1.15.

The price, p₀, of the good that would be obtained at the point of intersection, E, of the aggregate demand curve, DD, and the aggregate supply curve, SS, would itself be the equilibrium price of the good. At p = p₀, the market demand and market supply of the good are equal, both being equal to q = q₀ in Fig. 1.15. That is why, here p = p₀ is the equilibrium price and q = q₀ is the equilibrium quantity demanded and supplied.

If assumes as:

(i) At any particular price, if the market de­mand for the good is greater than the market supply, then the dissatisfied buyers would be willing to pay a higher price for the good and

(ii) At any particular price, if the market supply of the good is greater than the market demand, then the dis­satisfied sellers (who cannot sell all they want to sell) would be willing to accept a lower price for the good, then the equi­librium that would be obtained at point E in Fig. 1.15 would be a stable equilibrium.

For, here, if for any reason, the price of the good be more or less than the equilibrium price, then the behavioural pattern of buyers and sellers mentioned above ensures that the price would again come back to the level of equilibrium price, i.e., the market equilibrium will be restored. The two assumptions men­tioned above are known as the behavioural assumptions.

The matter is illustrated with the help of Fig. 1.15. Here, if the price of the good be less than p₀, if it is p₁ < p₀, then the quantity demanded would be greater than the equilibrium quantity, q₀, and the quantity supplied would be less than q₀.

It is got because of the laws of demand and supply. As a result, there would be excess demand—demand in excess of supply—in the market. At p = p₁, the quantity of excess demand would be FG. In this case, the buyers are not able to buy what they want to buy, and so they would be willing to pay a higher price; consequently, the price of the good would be increasing from pi till it becomes equal to p₀.

As price increases from p₁, the quantity demanded would fall and the quantity supplied would rise leading to a fall in excess demand, and, when p rises to the level of p₀, the whole of excess demand would be wiped out and the market would be in equilibrium.

On the other hand, if the price of the good is p = p₂ > p₀, then supply in the market would be in excess of demand, i.e., there would be a negative excess demand in the market. In this case, the sellers would not be able to sell what they want to.

As a result, they would be willing to accept a lower price, and p would be falling. As p falls from p₂, supply would fall and demand would rise, leading to a fall in excess supply. This would go on till p falls to the level of p₀ and the market equilibrium is restored.

It is discussed above how the price is determined in a perfectly competitive market through the process of interaction between the demand and supply for the good. It is also seen when and why the market equilibrium may be considered to be stable.