Perfect competition is compatible only with increasing cost situation, In other words, a perfectly competitive firm reaches equilibrium only when MC is rising. A competitive firm never reaches equilibrium when MC is falling (i.e., when the firm operates under decreasing cost condition) or when MC is constant (i.e., constant cost condition).
Thus, perfect competition and decreasing cost or constant costs are incompatible. Only under increasing cost i.e., only when MC is rising, are the conditions for equilibrium (i.e., MC = MR and MC must be rising) are satisfied.
However, a monopolist may reach equilibrium not only when MC is rising but also in cases where MC is falling or constant.
In other words, under any cost condition, i.e., whether MC is rising or falling or remaining constant, a monopoly reaches equilibrium provided the following two conditions are fulfilled:
ADVERTISEMENTS:
i. MC = MR
ii. Slope of MC > slope of MR
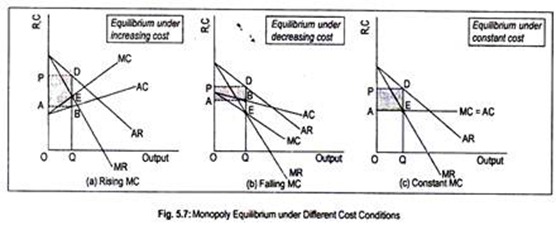
Under increasing cost, monopoly equilibrium, just like perfect competition, is possible. In this case, MC and AC curves are rising. In Fig. 5.7(a), E is the equilibrium point since both FOC and SOC are fulfilled at this point. The monopoly firm gets supernormal profit to the extent of ABDP by selling OQ output at the price OP.
If the monopoly firm operates under decreasing cost, it’s MC and the AC curves must be falling. Because of the fulfilment of FOC and SOC for equilibrium, the monopolist earns supernormal profit to the tune of ABDP.
ADVERTISEMENTS:
Under constant cost condition, MC curve becomes horizontal and coincides with the AC curve. Point E is the equilibrium point since, at that point, not only MC = MR but also the slope of MC > slope of MR. Anyway, the monopolist earns supernormal profit of AEDP amount by selling OQ output. This situation is incompatible with equilibrium under perfect competition.
So we can conclude that a monopolist may reach equilibrium under any cost conditions. He will attain equilibrium even if MC is falling or constant.