The following points highlight the seven limits to the power of a monopolist.
Limit # 1. Potential competition:
Only in rare cases is new entry absolutely barred. Patents, copyrights and government monopolies are possibly the only cases where new competitors cannot come.
In other cases possibility of competition exists and too high prices will tempt newcomers into the field. If dynamic entrepreneurs enter the monopolised industry, competition may be restored.
Limit # 2. Substitutes:
In reality almost every commodity has some substitutes. The monopolist can maintain his position only so long as the substitutes of the monopolised commodity are readily available. But if the monopoly price is too high people will begin to use less satisfactory substitutes (e.g., kerosene oil or gas for electricity). The monopolist, therefore, charges less than the highest possible price.
Limit # 3. Public Opinion:
ADVERTISEMENTS:
In democratic countries public opinion is always an important factor. Very high prices may induce the public to take retaliatory action (e.g., boycott) or induce the government to control the monopoly by law or nationalise it. Monopolists now-a-days take steps to keep the public satisfied. The best way of doing so is to charge fair prices. Consumers’ resistance may reduce price.
Limit # 4. Legislation:
In the case of public utility services, like gas or electric supply, the government, by law, limits the prices which can be charged.
Limit # 5. Consumers’ Surplus:
The monopolist must consider the consumers’ surplus obtained from the commodity. The monopolist cannot fix his price above the consumers’ surplus.
Limit # 6. Countervailing Power:
The monopolist buys raw materials, etc. from other producers. The monopolist pay-wages to their workers. It is found that the power of the monopolist is curtailed by the power of the suppliers of goods and of trade unions. This is called countervailing power.
Limit #7. Price elasticity of Demand:
ADVERTISEMENTS:
The ultimate limit to the power of a monopolist is set by price elasticity of demand for the product of the monopolist. In this context A. P. Lerner has related to the degree of monopoly power. This point will be explained fully freely in the context of profit curves.
Example 1:
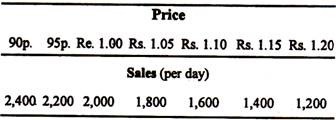
You have sole authority to sell sandwiches in Eden Gardens during a test match. Each costs 50 p. (including all relevant costs such as that of your labour).
From previous experience your best estimate of the demand is the following:
Your aim is to maximise your profit.
Assuming your estimate to be accurate:
(a) How many sandwiches would you sell in a day and at what price?
(b) Suppose one hour before you leave you find that you have 400 sandwiches left which will be inedible at the end of the afternoon. Your estimates have proved wrong.
You now estimate that the following demand schedule faces you:
What price would you now charge and how many (if any) sandwiches would be left unsold?
Solution:
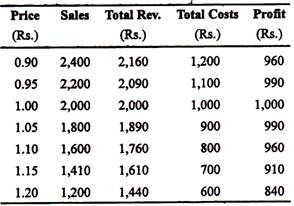
(a) If the object is to maximise profit, then this stage is reached when the difference between total revenue and total costs is at its greatest.
Profit is maximised at Rs. 100 (10,000 p.) and the price necessary to produce that profit is Re. 1.00 and the number of sandwiches sold at that price is 2,000.
(b) 400 sandwiches are left. These have already been produced at a cost of 400 x 50 p. = Rs. 200. A loss is inevitable and a price must be fixed to give the greatest total revenue (and, hence, the smallest total less). Given the demand schedule, the total revenue will be maximum when 300 units are sold at a price of 40 paise per unit. So 100 sandwiches will be left unsold and the firm will follow the policy of loss minimisation.
Example 2:
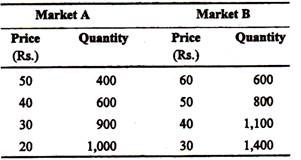
A monopolist has two markets and the demand schedules in them are as follows:
ADVERTISEMENTS:
He wants to sell 1,400 units. His TC = Rs. 30,000. What price will he set in the two markets and why?
Solution:
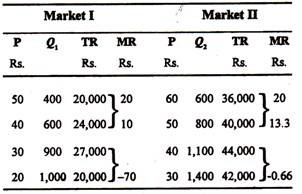
A discriminating monopolist reaches equilibrium and hence maximises profit when he equates the marginal revenue(s) in both the markets, i.e., MR1 = MR2. If this condition holds total revenue will be maximum and revenue maximisation subject to cost constraint implies profit maximisation. So we may calculate total revenue from each market for different price-quantity combinations and then the corresponding MR.
ADVERTISEMENTS:
This is done in the following table:
So when the firm sells 600 units in market I, at a price of Rs. 40 per unit and 800 units in market II at a price of Rs. 50, MR1 – MR2 and total revenue is Rs. 24,000 + Rs. 40,000 = Rs. 64,000 which is maximum. No other combination of Q1 and Q2 will yield the same total revenue and hence raise profit further.