The following points highlight the top four methods of evaluating and ranking profitability of investment projects. The methods are: 1. Pay Back Period (PBP) Method 2. Average Annual Rate of Return (AARR) 3. Net Present Value (NPV) 4. Internal Rate of Return (ARR).
Method # 1. Payback Period Method (PBP):
The payback period method is concerned with the recoupment (return) of the original investment made in a project. It lays emphasis on calculating the length of time it would take to recover the original investment. It involves calculation of the cash flows which would arise from investment in each year of the life of a project.
These cash flows are accumulated year by year till the time they equal the amount of the original investment made in the project. The length of time it takes to obtain the necessary cash flows equal to the original investment, determines the payback period for the project. PBP is also used to rank projects. For example, projects which repay within 3 years are preferred to those which take longer to pay back.
For example, if a project requires an annual investment of Rs. 25,000 crores and is expected to generate an annual cash inflow of Rs. 5,000 crores for 10 years, the payback period can be calculated as under;
ADVERTISEMENTS:
Pay Back Period (PBP) = Initial Investment/Annual, Cash Inflow
Or P = C/A1
Where, P = Pay Back Period;
С = Initial Investment or the cost of capital project; and
ADVERTISEMENTS:
A1 = Annual Cash Inflow
Or, P = 25,000/5,000 = 4
Thus, the PBP of this project is 4 years.
Accept or Reject Criterion:
PBP is used as a criterion to accept or reject an investment proposal. PBP calculated for a proposal is to be compared with some predetermined target period. If PBP is less than the target period, the proposal may be accepted. If PBP is more than the target period, the proposal may be rejected. By this method, proposals may be ranked. The lower the PBP, the more profitable the projects proposal.
Merits of Payback Period Method:
ADVERTISEMENTS:
The merits of this method are as follows:
1. This method is very easy to understand, calculate and apply.
2. Under this method, the firm can judge the tied-up of its funds and the risk period relating to its various projects.
3. This method emphasises on early returns and neglects distant returns.
4. This method takes less time in the calculation of project proposals so that the cost of analysis is low.
5. It is a more appropriate method for future planning in a fast changing industrial environment because it considers uncertainty in investment decisions.
6. This method is also useful when the firm does not want to take risk or early return on its investment or where the risk of obsolescence is high.
Weaknesses of Payback Period Method:
This method has the following shortcomings:
1. This method is based on the assumption that capital investment of short PBP is superior to capital investment of long PBP. But this is not always true.
ADVERTISEMENTS:
2. This method ignores those cash flows that arise after the payback period.
3. It does not measure the return on capital investment.
4. This method does not consider the timing of the occurrence of cash flows that arise from the project.
5. This method does not consider the time-value of money and neglects opportunity cost of funds.
ADVERTISEMENTS:
6. This method ignores those cash flows which arise from the sale of useless and discarded material after the project is finished.
7. It is not an appropriate method of measuring the profitability of an investment project because it does not consider all cash flows from the project.
Method # 2. Average Annual Rate of Return (AARR):
This method is based on the accounting concept of return on investment or rate of return. It refers to the percentage of the annual net income earned on the average funds invested in a project. The annual return of a project is the percentage of net investment in the project.
It can symbolically be expressed as follows:
ADVERTISEMENTS:
AARR = Average Annual Return/Average Investment in the Project x 100
For example, if average annual return of a project is Rs.10,000 while the initial cost of project is Rs.1, 0, 000, the annual rate of return will be as under:
AARR= 10,000/1,00,000 x 100
Thus, the average rate of return is 10%.
The calculation of AARR consists of the following three stages:
1. To subs-tract initial investment from gross total income during the life of the project.
ADVERTISEMENTS:
2. To divide net income by life years of the project for achieving per year average income.
3. To divide average annual income by initial investment and obtain return on investment.
Accept or Reject Criterion:
AARR is compared with the cut off or the pre-determined rate of return. If AARR is more than the predetermined rate of return, the project will be accepted otherwise rejected.
Merits of Average Annual Rate of Return:
1. This method is easy to understand and calculate.
2. It is based on accounting data that are always available.
3. It is contrary to the payback period method. It considers all the benefits arising out of the proposal throughout its life.
Limitations of Average Annual Rate of Return:
ADVERTISEMENTS:
In spite of the above merits, this method has the following limitations:
1. This method does not consider the time value of money. It gives equal importance to all returns of the project arising throughout the whole period.
2. This method is unable to compare the projects of different time periods.
3. It is not based on cash flows but on accounting profit.
4. The use of average profit is misleading because it does not consider year-to-year pattern of profits.
Method # 3. Net Present Value Method (NPV):
The net present value (NPV) method is an important criterion for project appraisal. Profitability of a project is evaluated by this method. It is also called as present value method. Net present value is calculated by using an appropriate rate of interest which is the capital cost of a firm. This is the minimum rate of expected return likely to be earned by the firm on investment proposals.
ADVERTISEMENTS:
To find out the present value of cash flows expected in future periods, all the cash outflows and cash inflows are discounted at the above rate. Net present value is the difference between total present value of cash outflows and total present value of cash inflows occurring in periods over the entire life of the project.
When the net present value is positive, the investment proposal is profitable and worth selecting. But if it is negative, the investment proposal is non-profitable and reject-able.
To calculate net present value index of different investment proposals, the following method can be used:
NPV= Total Present Value of All Cash Flows/ Initial Investment
NPV method considers the time value of money. It compares time value of cash flows.
NPV = Present value of Gross Earnings – Net Cash Investment NPV can be found out from the following formula:
ADVERTISEMENTS:
NPV= A1/(1+ r)1 + A2/ (1 + r)2 + A3 (1 + r)3 + …..An/ (1+r)n – C
Where A1, A2, A3 etc. are the cash inflows at the end of first, second and third year respectively
n = Expected life of investment proposals;
r = Rate of discount which is equal to the cost of capital;
С = Present value of costs.
Thus, NPV = Sum of Discounted Gross Earnings – Sum of Discounted Value of Cost For example, if the initial investment cost of a project is Rs.100 crores, cash inflow in the coming years is Rs.125 crores and the market rate of interest is 10% p.a., NPV will be as follows:
NPV = 125/ (1 + 0.10)1 – 100
= 125 x 10/11-100
= 113.64-100=13.64
Accept or Reject Criterion:
The decision criterion relating to NPV may be as under:
(a) If NPV > 0, the project is profitable.
(b) If NPV < 0, the project will not be profitable.
(c) If NPV = 0, the project may or may not be started.
If the decision is to be taken between two projects, the project with high positive NPV would be selected rather than the other.
Merits of NPV:
NPV method has the following merits:
(i) This method considers time value of money.
(ii) It considers the cash flows of the project in different time periods,
(iii) It is more scientific than traditional methods.
(iv) NPVs of different projects can be added to arrive at the cumulative NPV for a business.
(v) Intermediate cash flows are reinvested at the discount rate.
(vi) The calculation of NPV allows expected change in discount rate.
(vii) The discount rate (r) used for discounting future cash flows is, in fact, the minimum necessary rate of return which consists of both net of return and premium required to set off the risk.
(viii) The discount rate applied in the NPV method is the capital cost of the firm.
(ix) The use of NPV is the most profitable in view of the maximum profit.
Demerits of NPV:
There are also some demerits of this method:
(i) It is difficult to calculate the profit cost with this method.
(ii) It is difficult to work out especially the cost of equity capital by this method.
(iii) It is not applicable without the knowledge of cost of capital.
(iv) It favours long-run projects.
(v) When projects with different investments are compared, this method does not give correct result.
(vi) Its assumption that the intermediate cash flows are reinvested on the capital cost of the firms is not always true.
(vii) This method gives different rankings in the case of complicated projects in comparison to other methods.
Method # 4. Internal Rate of Return (IRR) Method:
This method refers to the percentage rate of return implicit in the flows of benefits and costs of projects. A. Marglin defines the internal rate of return (IRR), “as the discount rate at which the present value of return minus costs is zero”. In other words, the discount rate which equates the present value of project with zero is called IRR.
Thus, IRR is the discount rate which equates the present value of cash inflows with the present value of cash outflows. IRR is also based on discount technique like NPV method.
Under this technique, the future cash inflows are discounted in such a way that their total present value is just equal to the present value of total cash outflows. It is assumed that the management has knowledge of the time schedule of occurrence of future cash flows but not of the rate of discount.
IRR can be measured as:
A1/ (1+ r) 1 + A2/ (1 + r) 2 + A3 (1 + r) 3 + …..An/ (1+r) n-C=0
Where, A1, A2 A3, etc. are the cash inflows at the end of the first, second and third year respectively. For example, if Rs.1,000 crores is invested in a project, they become Rs.1,200 crores at the end of the first year. Now the rate of return is calculated as follows:
C=A1/ (1+r) 1
Where, 1= Cash outflow or initial capital investment;
A1= cash inflow at the end of First year;
R= rate of return obtained from investment.
Thus, Rs.1,000= Rs.1,200/ (1+r)1
Or, 1,000+1,000 r = 1,200
Or, 1,000 r = 1,200-1,000
Or, 1,000 r = 200
r = 200/ 1, 00= 0.20 or 20%
If the return is obtained for more than one year, the rate of return can be calculated as under:
C=A1/ (1+ r) 1 + A2/ (1 + r) 2 + A3 (1 + r) 3 + …..An/ (1+r) n
Accept or Reject Criterion:
A capital project is acceptable only when its internal rate of return (IRR) is more than the desired rate of return. It the relative profitability of the first project is higher than the second, the first will be superior and will be selected. If the net present values of two alternative projects are given, the choice of the projects will depend on the discount rate.
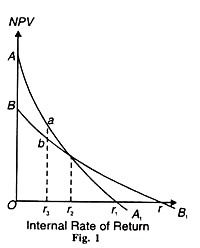
This is illustrated in Figure 1 where the rate of discount is measured along the horizontal axis and NPV on the vertical axis.
The curve AA1 depicts investment of project A and the curve BB1 of project B. The IRR of project В is higher than that of project A because the discount rate Or is higher than Or1. At Or2, the IRR of both the projects is equal. But if the discount rate falls below Or2 to Or3, projects will be chosen because its NPV is higher by ba. Making a choice between two projects on the basis of changes in the discount rate is called switching and re-switching.
Merits of IRR Method:
This method has the following merits.
1. This method does not consider the time-value of money.
2. The calculation of cost of capital is not an essential condition for using this method.
3. It considers the cash flows occurring over the entire period of the project.
Limitations of IRR Method:
But this criterion has certain limitations:
1. Once a rate of return is assumed for the calculation of the profitability of a project, it is not possible to change it.
2. It is difficult to calculate the rate of return on a long-gestation project which does not yield benefits for a number of years.
3. If projects are mutually exclusive, this criterion favours that project which has a lower capital cost than others Thus it cannot be applied to highly capital-intensive projects.
4. The use of IRR for public investment does not lead to correct decisions because the definition of IRR implies that intermediate receipts and outlays are also discounted at the internal rate. But it is not possible to discount intermediate benefits and costs of public investment at the internal rate of return.
5. There are often such projects on which the entire investment outlay cannot be made in the first period. It becomes difficult to calculate IRR in all such cases.
6. The IRR criterion is suitable for such investment projects which are wholly independent of others. But public investments are not independent of each other. Often they are alternatives. Therefore, it is difficult to make a choice between two alternative investments on the basis of their alternative internal rates of return.
7. Layard points out the problem of capital rationing where projects cannot be selected on the basis of ranking in order of rate of return. Such projects can only be selected on the basis of their net present value.
Relation between NPV and IRR:
The relation between NPV and IRR is also depicted in Figure 2. As NPV falls, the discount rate increases and a situation arise when NPV becomes negative. The rate at which NPV changes from positive to negative is the IRR. That project will be selected whose IRR is higher than its discount rate.
So the right criterion for the choice of a project is r > i. This is illustrated in the figure where IRR is taken as 10 per cent and the discount rate as 5 per cent in the case of project A. This project will be selected for development as long as its NPV > 0 and г (10%) > i (5%).
If two projects are Rate of Discount complex, these two criteria can give different results. But for the majority of projects, they are interchangeable. However, difficulties arise when two or more projects have to be compared and their lengths of life and capital investments differ.
Of the two criteria, NPV is more commonly used for project valuation in private and public sectors. But the NPV criterion is technically superior, since the IRR can give an incorrect result in special circumstances.
Conclusion:
NPV and IRR are different from each other. NPV is an absolute amount while IRR is a rate of return. Therefore, it is no use in comparing the ranking of investment projects with them. The projects should be evaluated by using these techniques separately.
Some investment proposals can be evaluated in a better way by the NPV criterion while others by the IRR criterion. The firm can then integrate the results of these techniques on the basis of the actual cost of capital for ranking the projects.